第四十四天| 卡尔网 52. 携带研究材料、518. 零钱兑换 II、377. 组合总和 Ⅳ

本文主要是介绍第四十四天| 卡尔网 52. 携带研究材料、518. 零钱兑换 II、377. 组合总和 Ⅳ，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

01背包问题卡尔网 52. 携带研究材料

题目链接：52 携带研究材料

题干：小明是一位科学家，他需要参加一场重要的国际科学大会，以展示自己的最新研究成果。他需要带一些研究材料，但是他的行李箱空间有限。这些研究材料包括实验设备、文献资料和实验样本等等，它们各自占据不同的重量，并且具有不同的价值。

小明的行李箱所能承担的总重量为 N，问小明应该如何抉择，才能携带最大价值的研究材料，每种研究材料可以选择无数次，并且可以重复选择。

• 输入描述：

第一行包含两个整数，N，V，分别表示研究材料的种类和行李空间 

接下来包含 N 行，每行两个整数 wi 和 vi，代表第 i 种研究材料的重量和价值

• 输出描述：

输出一个整数，表示最大价值。

思考：此题为完全背包问题。01背包和完全背包唯一不同就是体现在遍历顺序上，所以直接针对遍历顺序分析。

01背包内嵌的循环是从大到小遍历，为了保证每个物品仅被添加一次。而完全背包的物品是可以添加多次的，所以要从小到大去遍历，保证物品可重复取，具体原因在01背包问题中讲过。

但此处物品和背包容量遍历顺序可以调换。因为dp[j] 是根据 下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的就可以。

若先遍历物品再遍历背包则代码如下：

// 先遍历物品，再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}

若先遍历背包再遍历物品则代码如下：

// 先遍历背包，再遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量for(int i = 0; i < weight.size(); i++) { // 遍历物品if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}cout << endl;
}

代码：

#include<iostream>
#include<vector>
using namespace std;//采用滚动数组存储的最大价值
int knapsack_1D(vector<int>& weight, vector<int>& value, int bagWeight) {//dp[j]表示背包空间为j的情况下，从所有物品里任取，能达到的最大价值vector<int> dp(bagWeight + 1, 0);for (int i = 0; i < weight.size(); i++)     //遍历物品for (int j = weight[i]; j <= bagWeight; j++)     //遍历背包重量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);return dp[bagWeight];  
}int main() {int bagWeight, objectNum;cin >> objectNum >> bagWeight;vector<int> weight(objectNum, 0);vector<int> value(objectNum, 0);for (int i = 0; i < objectNum; i++) {cin >> weight[i];cin >> value[i];}cout << knapsack_1D(weight, value, bagWeight) << endl;system("pause");
}

Leetcode 518. 零钱兑换 II

题目链接：518 零钱兑换 II

题干：给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

假设每一种面额的硬币有无限个。 

题目数据保证结果符合 32 位带符号整数。

思考：动态规划。由于不同面额的硬币可取多次，因此本题为完全背包的类似问题。

• 确定dp数组以及下标的含义

dp[j]：硬币总额为i的组合个数

• 确定递推公式

dp[j] 就是所有的dp[j - coins[i]]（考虑coins[i]的情况）相加。所以递推公式：dp[j] += dp[j - coins[i]];

• dp数组如何初始化

从递推公式可以看出，如果dp[0] = 0 的话，后面所有推导出来的值都是0。

下标非0的dp[j]初始化为0，这样累计加dp[j - coins[i]]的时候才不会影响真正的dp[j]

• 确定遍历顺序

本题背包（硬币总额）以及物品（硬币）的先后遍历顺序与纯完全背包不同，后者求得装满背包的最大价值是多少，和凑成总和的元素有没有顺序没关系，即：有顺序也行，没有顺序也行！

但本题要求凑成总和的组合数，元素之间明确要求没有顺序。因此要分别尝试先遍历物品（硬币）以及先遍历背包（硬币总额）两种情况。

---

尝试先遍历背包（硬币总额）后遍历物品（硬币）会发现求出的是排列个数不是组合个数。举例

硬币面值只要1和2，要求硬币总金额为3的组合个数。不难得到dp[1] = 1; dp[2] = 2;

在处理dp[3]时出现问题，按递推公式dp [3] = dp [2]  + dp[1]，结果为3，而实际只有2种组合。

多出来的一种从哪来的呢？

从dp[2]：总金额为2组合分别为 {1，1}以及{2}，dp[1]：总金额为1组合为{1}

按递推公式则将组合{1，2}和{2，1}都算一种组合，而这两组合一样。

而先遍历物品（硬币）后遍历背包（硬币总额）可行。

• 举例推导dp数组

输入: amount = 5, coins = [1, 2, 5] ，dp状态图如下：

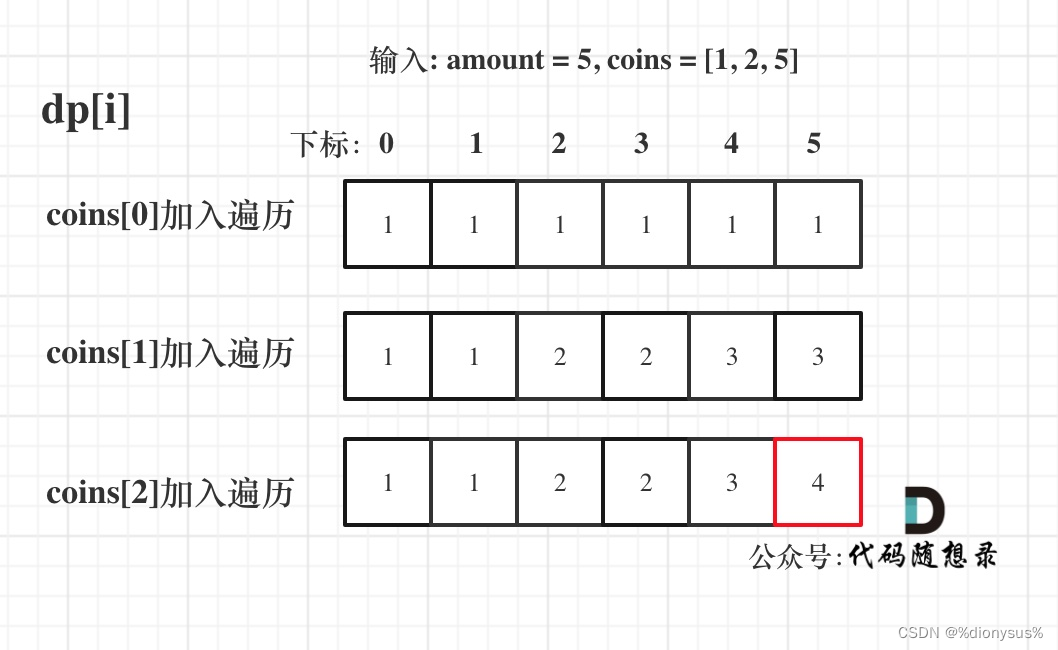
代码：

class Solution {
public:int change(int amount, vector<int>& coins) {vector<int> dp(amount + 1, 0);      //dp[i]表示硬币总额为i的组合个数dp[0] = 1;for (int i = 0; i < coins.size(); i++)          //遍历硬币for (int j = coins[i]; j <= amount; j++)    //遍历硬币总额dp[j] += dp[j - coins[i]];return dp[amount];}
};

Leetcode 377. 组合总和 Ⅳ

题目链接：377 组合总和 Ⅳ

题干：给你一个由 不同 整数组成的数组 nums ，和一个目标整数 target。请你从 nums 中找出并返回总和为 target 的元素组合的个数。

题目数据保证答案符合 32 位整数范围。

请注意，顺序不同的序列被视作不同的组合

思考：动态规划。本题和上题几乎一模一样，唯一的区别在于本题顺序不同的序列被视作不同的组合，因此只需要确定遍历顺序时将顺序修改为先遍历背包容量后遍历物品即可。

由于本题有测试案例会超过int表示范围的情况，因此在内层循环的判断语句还要加上判断条件dp[i] < INT_MAX - dp[i - nums[j]]。

代码：

class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<int> dp(target + 1, 0);      //dp[i]表示从数组中任取数字能达到累加和i的排列个数dp[0] = 1;for (int i = 0; i <= target; i++)           //遍历累加和for (int j = 0; j < nums.size(); j++)   //遍历数组if (i >= nums[j] && dp[i] < INT_MAX - dp[i - nums[j]])      //去处案例超过int表示范围的情况dp[i] += dp[i - nums[j]];return dp[target];}

自我总结：

•  确定遍历顺序的依据：递推公式，数组内元素是否可重复取以及题干要求的是存在，组合还是排列。

这篇关于第四十四天| 卡尔网 52. 携带研究材料、518. 零钱兑换 II、377. 组合总和 Ⅳ的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---