本文主要是介绍pclpy Ransac平面分割算法输出的索引从点云中提取点云的子集,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
pclpy Ransac平面分割算法输出的索引从点云中提取点云的子集
- 一、算法原理
- 二、代码
- 三、结果
- 1.`sor`统计滤波
- 2.`Ransac`内点分割平面
- 3.`Ransac`外点分割平面
- 四、相关数据
一、算法原理
1、Ransac介绍
RANSAC(RAndom SAmple Consensus,随机采样一致)算法是从一组含有“外点”(outliers)的数据中正确估计数学模型参数的迭代算法。“外点”一般指的是数据中的噪声,比如说匹配中的误匹配和估计曲线中的离群点。所以,RANSAC也是一种“外点”检测算法。RANSAC算法是一种不确定算法,它只能在一种概率下产生结果,并且这个概率会随着迭代次数的增加而加大(之后会解释为什么这个算法是这样的)。
RANSAC主要解决样本中的外点问题,最多可处理50%的外点情况。
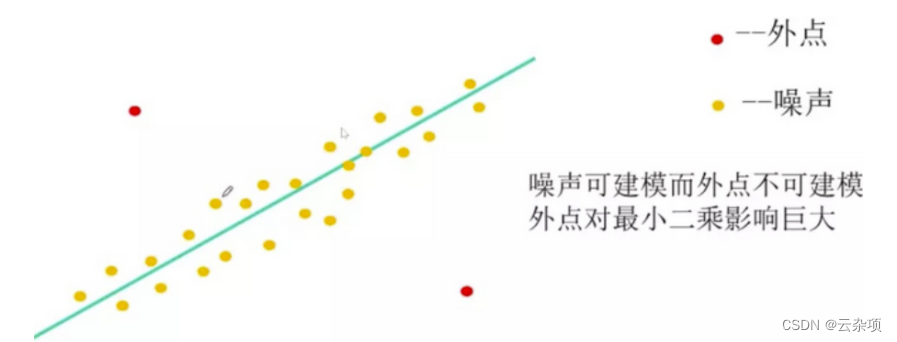
范例
可以简单总结为以下步骤:
N:样本个数 K:求解模型需要的最少的点的个数(对于直线拟合来说就是两个点,对于计算Homography矩阵就是四个点)
随机采样K个点
对该K个点拟合模型
计算其他点到拟合模型的距离。如果小于一定阈值,该点被当作内点,统计内点个数
重复M次,选择内点数最多的模型
利用所有的内点重新估计模型(可选)
RANSAC用于拟合直线:
1.随机选取K = 2 ,2个点:
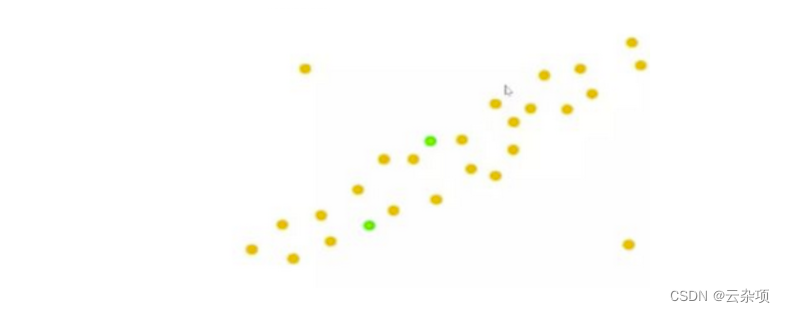
2.拟合一条直线:

3.统计内点个数,内点为绿色,此时的内点个数为9(小于一定阈值计算为内点):
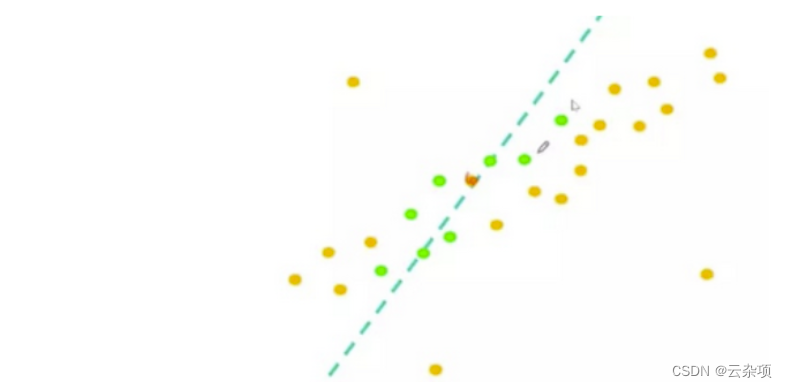
4.重复上述过程M次,找到内点数最大的模型(继续随机选点根据k=数目进行选点):
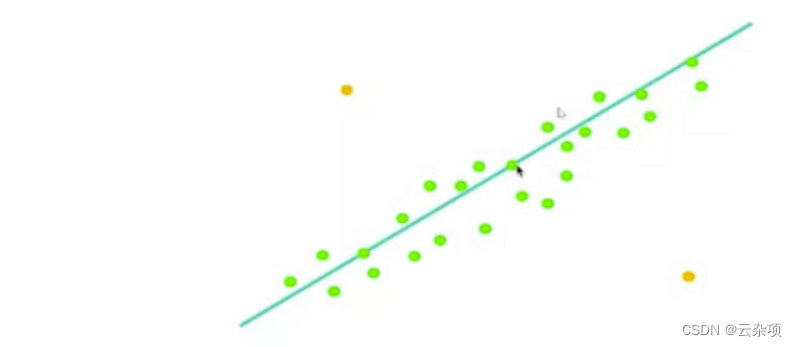
5.利用所有的内点重新估计直线:

二、代码
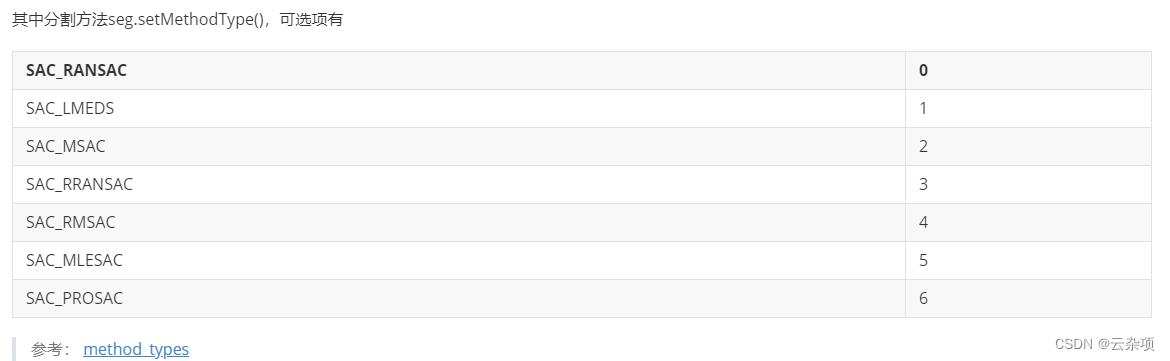
from pclpy import pcldef compareCloudShow(cloud1, cloud2):"""Args:在一个窗口生成2个窗口可视化点云cloud1: 点云数据1cloud2: 点云数据2"""viewer = pcl.visualization.PCLVisualizer("viewer") # 建立可刷窗口对象 窗口名 viewerv0 = 1 # 设置标签名(0, 1标记第一个窗口)viewer.createViewPort(0.0, 0.0, 0.5, 1.0, v0) # 创建一个可视化的窗口viewer.setBackgroundColor(0.0, 0.0, 0.0, v0) # 设置窗口背景为黑色single_color = pcl.visualization.PointCloudColorHandlerCustom.PointXYZ(cloud1, 255.0, 0, 0.0) # 将点云设置为红色viewer.addPointCloud(cloud1, # 要添加到窗口的点云数据。single_color, # 指定点云的颜色"sample cloud1", # 添加的点云命名v0) # 点云添加到的视图v1 = 2 # 设置标签名(2代表第二个窗口)viewer.createViewPort(0.5, 0.0, 1.0, 1.0, v1) # 创建一个可视化的窗口viewer.setBackgroundColor(255.0, 255.0, 255.0, v1) # 设置窗口背景为白色single_color = pcl.visualization.PointCloudColorHandlerCustom.PointXYZ(cloud2, 0.0, 255.0, 0.0) # 将点云设置为绿色viewer.addPointCloud(cloud2, # 要添加到窗口的点云数据。single_color, # 指定点云的颜色"sample cloud2", # 添加的点云命名v1) # 点云添加到的视图# 设置点云窗口(可移除对点云可视化没有影响)viewer.setPointCloudRenderingProperties(0, # 设置点云点的大小1, # 点云像素"sample cloud1", # 识别特定点云v0) # 在那个窗口可视化viewer.setPointCloudRenderingProperties(0, # 设置点云点的大小1, # 点云像素"sample cloud2", # 识别特定点云v1) # 在那个窗口可视化viewer.addCoordinateSystem(1.0) # 设置坐标轴 坐标轴的长度为1.0# 窗口建立while not viewer.wasStopped():viewer.spinOnce(10)if __name__ == '__main__':# 读取点云数据cloud = pcl.PointCloud.PointXYZ()reader = pcl.io.PCDReader()reader.read('res/table_scene_lms400.pcd', cloud)print('点云数目:', cloud.size())# 创建sor滤波器 参考 pclpy SOR去除异常值(统计滤波) pclpy专栏中cloud_filtered = pcl.PointCloud.PointXYZ()sor = pcl.filters.StatisticalOutlierRemoval.PointXYZ() # 创建sor处理对象sor.setInputCloud(cloud) # 将cloud处理sor.setMeanK(50) # 每个点要分析的邻居数sor.setStddevMulThresh(1.0) # 距离查询点的平均距离大于1个标准差的点都将被标记为离群值并删除sor.filter(cloud_filtered) # sor处理后的点云保存在这里(内点)# 可视化滤波效果compareCloudShow(cloud, cloud_filtered) # 参考 pclpy 可视化点云(多窗口可视化、单窗口多点云可视化) pclpy在专栏中coeffs = pcl.ModelCoefficients() # 存储估计的平面参数inliers = pcl.PointIndices() # 存储平面模型的内点索引# 创建分割objectseg = pcl.segmentation.SACSegmentation.PointXYZ()# 可选项seg.setOptimizeCoefficients(True)# 设置seg.setModelType(0) # 0平面模型seg.setMethodType(0) # 表示 RANSAC 算法 open3d 平面分割(Ransac算法) 专栏open3dseg.setMaxIterations(1000) # 设置 RANSAC 算法的最大迭代次数为 1000。seg.setDistanceThreshold(0.01) # 设置平面模型的距离阈值为 0.01,用于判断点是否为内点(inliers)# 创建滤波objectextract = pcl.filters.ExtractIndices.PointXYZ()nr_points = cloud_filtered.size() # 获得点云数目while cloud_filtered.size() > nr_points * 0.3:# 从保留的点云中分割最大的平面成分seg.setInputCloud(cloud_filtered) # 将滤波后的点云数据设置为分割器的输入seg.segment(inliers, coeffs) # 分割后的内点索引保存在 inliers 中,将平面模型系数保存在 coeffsif len(inliers.indices) == 0:print('无法对给定数据集估计平面模型。')break# 提取内点(平面成分)extract.setInputCloud(cloud_filtered) # 从点云中提取指定索引的点 和 open3d 中的select_index_by()一样extract.setIndices(inliers) # 将计算索引进行装填extract.setNegative(False) # 获得内点cloud_p = pcl.PointCloud.PointXYZ()extract.filter(cloud_p)# 可视化提取出来的平面compareCloudShow(cloud_filtered, cloud_p)print("点云数目:", cloud_p.size())# 再次滤波,提取外点(非平面成分)extract.setNegative(True) # 获得外点cloud_f = pcl.PointCloud.PointXYZ() extract.filter(cloud_f)cloud_filtered.swap(cloud_f) # 等价于cloud_filtered = cloud_f
三、结果
1.sor统计滤波
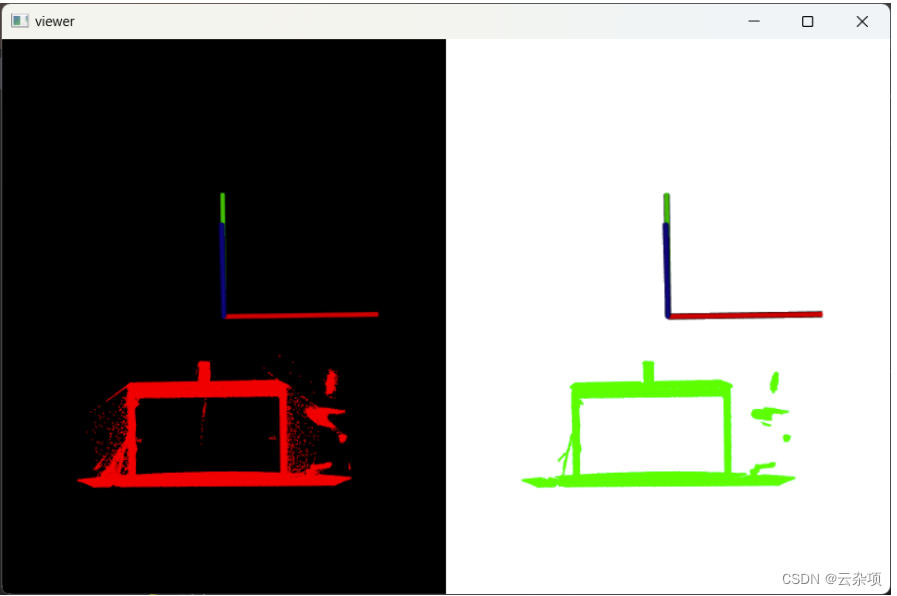
2.Ransac内点分割平面
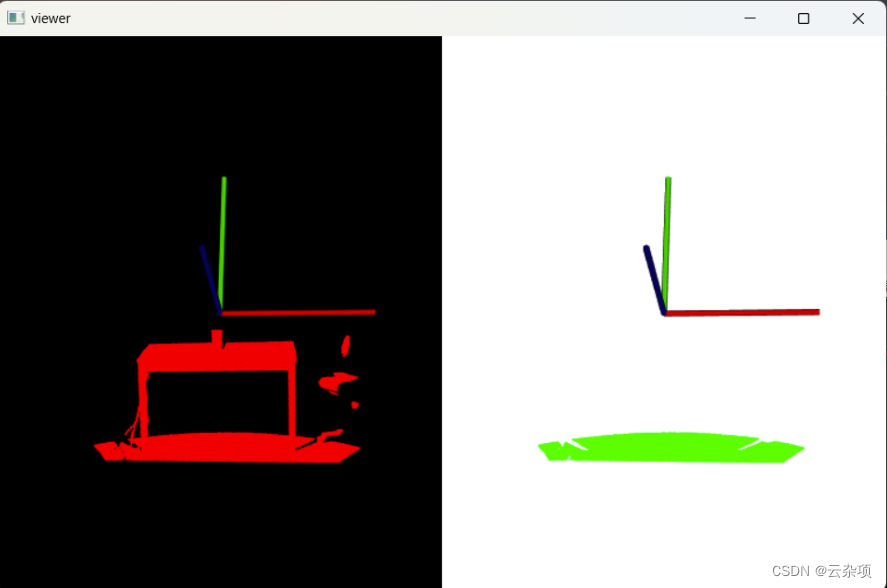
3.Ransac外点分割平面
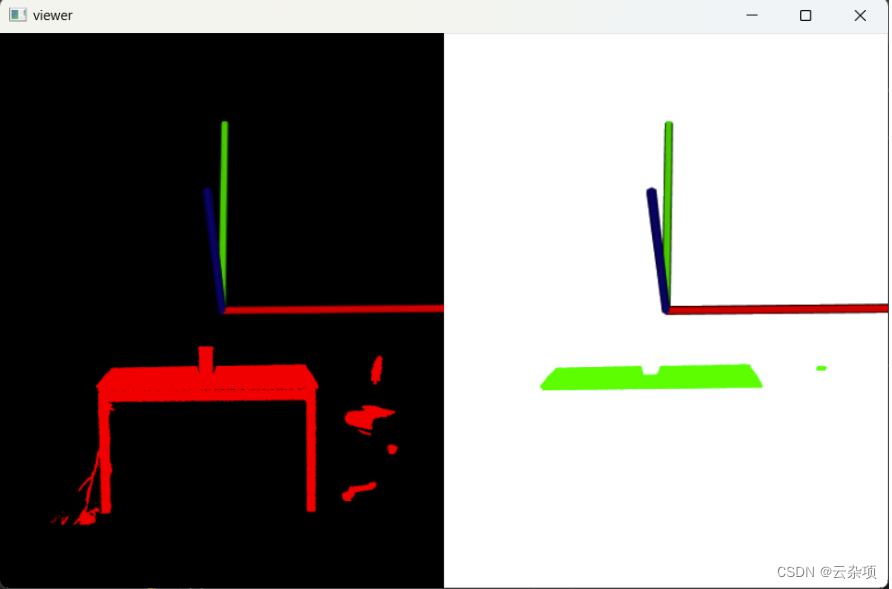
四、相关数据
pclpy SOR去除异常值(统计滤波):pclpy SOR去除异常值(统计滤波)-CSDN博客
pclpy 可视化点云(多窗口可视化、单窗口多点云可视化):pclpy 可视化点云(多窗口可视化、单窗口多点云可视化)-CSDN博客
open3d 平面分割(Ransac算法) open3d 平面分割(Ransac算法)-CSDN博客
这篇关于pclpy Ransac平面分割算法输出的索引从点云中提取点云的子集的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








