【梳理】数据库系统概论 第6章 关系数据理论 6.2 规范化（未完待续）

教材：王珊 萨师煊 编著 数据库系统概论（第5版） 高等教育出版社
注：文档高清截图在后

（未完待续）

6.2 规范化

1、函数依赖要求属性间满足一定的函数关系：自变量确定后，相应的因变量也要唯一确定。即：设R(U)是属性集U上的一组关系模式，U有子集X、Y。若对于R(U)的任意一个关系r，不存在两个元组在X上的属性值相等却在Y上的属性值不等，就称X函数确定Y或Y函数依赖于X，记作X→Y。函数依赖和别的数据依赖一样，是语义范畴的概念，只能根据语义来确定函数依赖。例如：“小说标题→小说作者”这个关系只有在无同名但正文不同的小说的情况下成立。如果允许相应的域中存在同名但内容不同的小说，就无法只根据标题确定作者（你又不保证是同一个作者写的两篇标题相同但正文不一的小说），就不能在这两个属性上定义函数依赖。
如果X→Y但 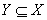，就说X→Y是平凡的函数依赖，否则称为非平凡的函数依赖。对任意关系模式，平凡函数依赖总是成立的，不反映新的语义。例如：对关系“剧组人员的经历”的属性建立函数依赖{导演，编剧}→{导演}。对关系中的任意元组，可以这样解读：如果元组对应的人员既是导演，又是编剧，那么自然能知道“此人是导演”一定成立，并没有反映多少新东西。类似地，如果此人不是导演、不是编剧，或不是导演、是编剧，或是导演、不是编剧，也会得到类似的结果：推不出任何新信息。如果不特别声明，默认一个依赖是非平凡的函数依赖。
如果X→Y，称X为该函数依赖的决定属性组，也称决定因素。注意：这里的“决定”指的是能够唯一确定值。即便两者在自然语言上没有直接关系，但是只要能够通过某种方法通过X确定Y的属性值，就称X为决定因素。
若X→Y且Y→X，就记为X←→Y。

2、如果X→Y，且对X的任一真子集X’，X’→Y都不成立，那么称Y对X完全函数依赖（Full functional dependency），记作 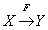。否则，即：若Y不完全函数依赖于X（属性集Y不完全由属性集X中的每一个分量确定），就称Y对X部分函数依赖（Partial functional dependency），记作 。
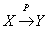例如：书名对ISBN是完全的函数依赖；（亚欧的部分国家和地区流通的）商品、（美加一带流通的）商品分别对EAN码、UPC完全函数依赖。


{姓名、身份证号、手机号码、身高}→{入住时间}不是完全函数依赖，因为一个人的身高不决定此人在酒店的入住时间。

3、如果X→Y（但 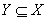不成立），Y→Z（但 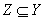不成立），则称Z对X传递函数依赖（Transitive functional dependency），记作 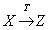。例如：某地下组织的数据库中存有关系“监视对象”，存在函数依赖：代号→身份证号，身份证号→工作单位。所以代号→工作单位是传递函数依赖。
但如果不限制 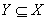不成立，那么X←→Y，实际上可以化简成直接函数依赖X→Z。例如：某企业新招收一批在读研究生进行项目合作，关系“工作信息”中，学号←→工号→工作内容，实际上存在直接函数依赖：学号→工作内容。

4、回忆：
2.1 关系数据结构及其形式化定义
若关系中某个（些）属性的值能够唯一标识一个元组而其真子集都不能，就称这部分属性为候选码（candidate key）。例如记录学生信息的一张二维表，只有学号是唯一的，其余信息都可能重复，那么学号属性为候选码。一个关系可以有多个候选码，一般只选一个作为主码（primary key）。最简单的情况下，候选码只包含一个属性。最极端的情况下，关系模式的全部属性都称为候选码，称为全码（all-key）。
2.3 关系的完整性
实体完整性规则 若属性（一个或一组）A是基本关系R的主属性，则A不能为空（null）。空值就是不知道、不存在或无意义（未定义）的值。
设K是R<U, F>中的属性或属性组。若 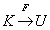，就说K是R的候选码（candidate key）。如果U部分依赖于K，即 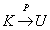，称K为超码。显然，候选码是拥有属性数量最少的超码，K的任意一个真子集都不是候选码；在候选码的基础上再添加属性，就成为超码。若候选码多于一个，就选其中一个为主码（primary key）。包含在任何一个候选码中的属性都称为主属性（prime attribute），其余的为非主属性（non-prime attribute）或非码属性（non-key attribute）。最简单的情况，单个属性就构成码；最极端的情况，全部属性都是码，称为全码（all-key）。可见，全体主属性的集合 = 拥有属性最多的候选码。主码是主属性的子集（不一定是真子集），主码也是候选码的子集。主属性不能为空，但可以允许重复。只有选做主码的属性（集）才整体不允许重复。例如：关系模式S（名字，ID，邮箱，任务）中，邮箱和ID可以各自都是码，也可以整体作为码。

5、关系模式R中，若属性（组）X不是R的码，但是别的关系模式的码，就称X是R的外部码（foreign key），也称外码。例如：R（国家（地区），省（州），市，机房编号），S（机房编号，服务器编号，主要任务），S的属性“机房编号”虽然不是S的码，但是是R的外码。

6、E.F.Codd在1971—1972年系统提出了1NF、2NF、3NF的概念，1974年Codd和Boyce共同提出了新的范式BCNF，1976年Fagin提出了4NF，后又有研究人员提出5NF。各种范式之间的关系是：

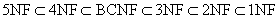
一个低一级范式的关系模式可以通过模式分解（schema decomposition）转换为若干个高一级的范式的关系模式的集合，这个过程叫做规范化（normalization）。

7、第二范式（2NF）：若R∈1NF，且每一个非主属性完全函数依赖于任何一个候选码，则R∈2NF。
如果一个关系模式不属于2NF，可能会出现以下问题：
（1）插入异常（insertion anomalies）。有的主属性会被选做主码或主码的一部分。由于存在不完全函数依赖于候选码的非主属性，当不决定该非主属性且为主码的组成部分的主属性为空时，插入就会失败。因为主码不允许为空（一个元组的主属性的值为空，后果也只是令该属性不再是主属性）。这就导致了其它应该插入的信息也一并无法插入。
例：关系模式R（学号、已选课程、学院、专业、年级），主码由（学号，已选课程）共同构成。某学生尚未选课，但已经被分入特定的专业。此时只想将该生的学号和专业写入数据库而将已选课程留空则插入失败。
（2）删除异常（deletion anomalies）。如果有非主属性不完全函数依赖于候选码，就意味着无论不依赖的那部分主属性取何值，这些非主属性都不受影响。特殊地，如果某些主属性被作为主码的一部分，且不影响这些非主属性，那么将这些主属性置空，这些非主属性也不受影响。然而，主码是不允许为空的，因此会删除失败并报错，或者导致整个元组被删除，即删除了不应该删除的信息。
例：取（1）中的R。当某学生将已选的唯一一门课程退选，但已选课程为主码的一部分，因此删除失败，或许也会导致描述该学生的整个元组一起被删除，导致其它信息（学院、专业、年级）一起丢失。
（3）更新异常（update anomalies）。由于存在不受部分主属性影响的非主属性，当这些主属性不同时，由于非主属性不受影响，这些非主属性就可以保持不变。这样就存储了大量冗余的数据。当这个非主属性也需要修改时，就要把这些重复的部分也一起修改，造成了修改的复杂化。如果SQL语句输入有误，就可能造成需要修改的地方遗漏，导致数据的完整性和相容性被破坏。
例：取（1）中的R。某学生从理学院的生物专业转到计算机学院的智能科学与技术专业，而且设计这个关系模式的人犯傻，“已选课程”属性限制了一个条目只能写一门课，而该生选了11门课且选课不变，于是其它四个属性不变的记录在这个关系模式中存储了11次。这11个元组的“学院”和“专业”属性的值也需要一并被修改，修改的工作量就比较大。
将只属于1NF的关系模式分解成若干个子关系模式，令全部子关系模式的非主属性都完全依赖于候选码，就得到了全部属于2NF的关系模式。当然，在子关系模式中，属性的“是否为主属性”这一性质可能会变化。修改后，原本会发生插入异常的输入数据不会全部发生插入异常，因为已经将应该添加的非主属性的信息与不决定这些非主属性的主属性从同一关系模式中分离了；原本会发生删除异常的数据不会全部发生删除异常，因为已经将不应被连带删除的非主属性的信息与需要置空的与这些非主属性无关的主属性从同一关系模式中分离了；原本会发生更新异常的数据不会全部发生更新异常；因为非主属性与无关的主属性已从同一关系模式中分离，只需要更新子关系模式中相应的数据即可，冗余数据与需要修改的数据都大大减少。
将关系模式R分离成S（学号，已选课程）和T（学号，学院，专业，年级）。对（1）中的例子而言，尚未选课时，可以先将该生的其它信息写入数据库。对（2），则在已选课程为空时，只有S中的条目被删除，T中是需要保留的学生信息，无需删除。对（3），只需要更改T中的元组，而对11条选课信息则无需变动。

8、第三范式（3NF）：若R∈1NF，且没有非主属性对码（候选码）传递函数依赖（X→Y→Z仅要求X是候选码，Z是非主属性（组）），则R∈3NF。可以证明R∈3NF时一定有R∈2NF。
如果一个关系不属于3NF，也有几率出现与不是2NF相似的问题。解决方案也是类似的：按照传递关系将关系模式分解为多个子关系模式。
9、BC范式（BCNF，修正第三范式，扩展第三范式）：若R∈1NF，如果X→Y但 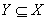不成立时X必含有码（必含有候选码），则R∈BCNF。也就是说，关系R的每一个决定因素都包含码时，R∈BCNF。可以证明R∈BCNF时一定有R∈3NF。

10、1NF到BCNF是在函数依赖的条件下对模式分解的程度的量度。如果一个模式中的关系模式都属于BCNF，那么在函数依赖的范畴内它已经彻底分离，已消除了插入异常和删除异常。