本文主要是介绍正定矩阵 Positive definite matrix,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Positive definite matrix
说道正定矩阵,这名字又能糊住很多人。心里默默念叨“我X,这是个什么矩阵,干嘛用的,名字这么叼”
首先,本来可能很浅显的数学概念,从原来的英文描述翻译成中文之后会变得更加抽闲!
我看了MIT的公开课视频才知道所谓的正定矩阵是 positive definite matrix。
下面是授课视频的link
http://v.163.com/movie/2010/11/3/P/M6V0BQC4M_M6V2B5J3P.html
blog符号说明: V’ 表示矩阵V的转置
x^2 表示x的平方
-------------------------------------------------------------------------------------------------------------------------------------------
首先回归到矩阵的本质,矩阵是什么,就是多元函数的系数一种很巧妙的表示方法!无他!
对于这些系数的探讨和研究直接可以分析出函数的特性。
首先由下面的问题引出positive definite matrix的定义
对于一个系数矩阵
A = [a b
c d];
列向量V = [x
y];
V' A V = [ax + cy, bx +dy] * V
= (ax+cy)*x + (bx+dy)*y
= ax^2 + dy^2 + (c+b)x*y;
想想,对于任意的x和y变量,我们能够找到适当的a b c d值,是不是可以把V'AV的值确定为大于等于0的?!
比方A = [1 0
0 1];
这样V' AV = x^2 + y^2; 任意的xy,该式子的值都大于等于0;
如果除开V = [0 ;0]这种情况,其余的地方都是大于0的。
这就是正定矩阵的来源!
正定矩阵的定义就是,对于V不等于零向量的任意向量,有矩阵A使得,V' AV > 0成立,我们把这样的矩阵A称作正定矩阵。
关于positive definite matrix的判定:
1. 矩阵特征值均大于0
2. 行列式的值大于0.
举例,下图中的待确定的矩阵,第二行第二列的元素未知,如果我们填入适当的数值,应该填写多大的数值可以使得该矩阵正定呢?
显然问题很简单,大于18即可。
如果是刚好等于18呢?我们把这种情况称为半正定——positive semi-definite matrix。
恩,既然是说函数V'AV的值在除开零向量出,任意的V均使得函数大于0,二元函数我们可以左图检验。
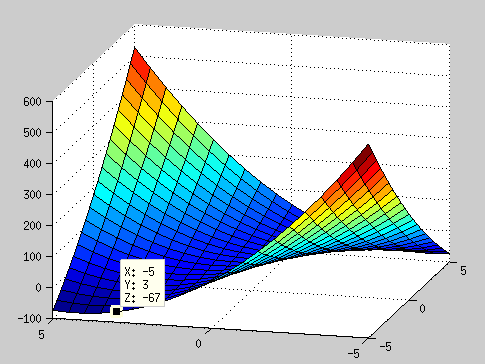
比方说这里矩阵A = [ 2 6
6 7];
很明显,这里的A是非正定的,对于变量V = [x1 x2],
观察该函数的图像,这个函数的图像像个马鞍,可以观察到,函数是有小于0的部分的。很好的印证了非正定矩阵。
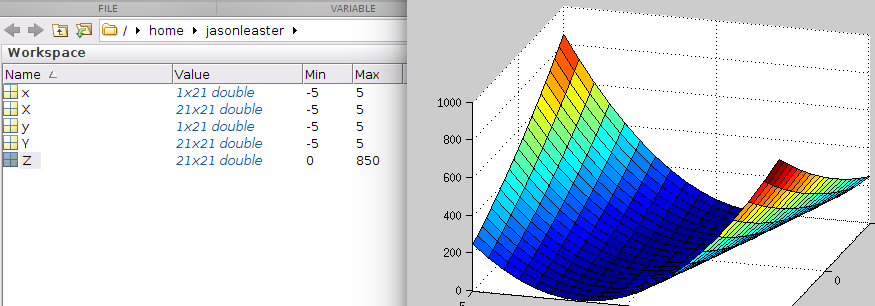
我们只需稍作A的调整,把7改成大于18的数值(比方说20),即可得到正定矩阵,函数的图像除开0点之外,对于所有V的取值,都大于0.
下面是函数图像,Z变量即函数值。我们可以直观的看出函数最小不小于0。
到现在应该明白了,正定矩阵干嘛用的?使得V' AV大于0。进一步的,我们可以利用函数求导的性质探究函数极值的情况。
这篇关于正定矩阵 Positive definite matrix的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!
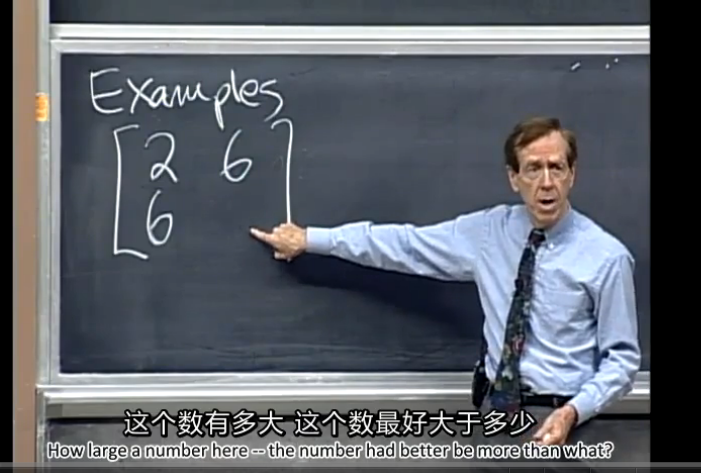



![[论文笔记]LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale](https://img-blog.csdnimg.cn/img_convert/172ed0ed26123345e1773ba0e0505cb3.png)


