【踏雪无痕的痕二】——小学一年级数学题窥探蝴蝶效应

本文主要是介绍【踏雪无痕的痕二】——小学一年级数学题窥探蝴蝶效应，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、背景介绍
二、思路&方案
三、过程
- 1.结果一致过程不一致带来的偏差
- 2.再举两个例子，你品一品
- 3.我曾经的培养计划背后的"力量"？
- 4.蝴蝶效应——混沌或非线性理论
- - 什么是蝴蝶效应？
- 5.内心深处的小恶魔(人性的使然)
四、总结

一、背景介绍

如果说"【踏雪无痕的痕一】——认知的心病"中开篇是认知上的开始，那么这一篇将是具体落实上的开始。

2013年-2017年，四年的时间我到底是如何变过来的？通过2018年-2020年的参与以及2021年-2023年三年的深化有了一定的理解，于是开启《踏雪无痕的痕》系列文章；通过系列文章想要做到：

1.将教育最高境界中踏雪无痕的痕明示出来，寻找自己的归路
2.自己也可以做到踏雪无痕
3.可以通过踏雪无痕让自己的孩子在未来大学毕业的时候，可以超过当初我计算机系阶段毕业的社会认可度
4.让中国万万家庭都可以做到成本很低的达到教育新阶梯

二、思路&方案

1.结果一致过程不一致带来的偏差
2.再举两个例子，你品一品
3.我曾经的培养计划背后的"力量"？
4.蝴蝶效应——混沌或非线性理论
5.内心深处的小恶魔(人性的使然)

三、过程

1.结果一致过程不一致带来的偏差

问题：连线题，1-5和五种物品进行连线
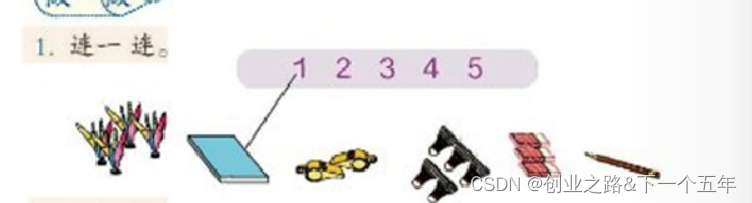
在这里插入图片描述

分析：两种方式最终结果如果都对的情况下，你是不确定孩子对于每一个数是否掌握边界足够清晰。

1.选择过程中用了排除法
2.选择过程中没有用排除法，而是非常明确连线的两方的一致性边界

2.再举两个例子，你品一品

2.1.小学语文中孩子写字出现的倒插笔？最终字是对的，但是笔画对了嘛？笔画的先后顺序对了嘛？
2.2.考试中的单选题？是选对了正确答案，还是其它错误答案也非常清楚哪里错了？

3.我曾经的培养计划背后的"力量"？

3.1.培养计划中，虽然整体资料在300G左右，但是这300G资料是老师从几百T资料中挑选出来的
3.2.这些资料那个在前，那个在后，学完那个要有什么总结，什么闭环反馈等都是有明确的要求的(符合PDCA原则)
3.3.通过师徒制(学习金字塔)、项目驱动(运用与知识相结合相辅相成)

4.蝴蝶效应——混沌或非线性理论

小学时候的知识理解停留在结果上、应试上，但是每次考试却能得很高的分，日积月累下去，孩子后面的知识越来越多还用应试的方式势必会越学越累；最终导致家长、老师都不清楚孩子成绩一落千丈甚至厌学等；为啥会有如此大的变化？

什么是蝴蝶效应？

“蝴蝶效应”是一种广为人知的概念，它描述了在一个动态系统中，一个微小的初始变化可能会在不经意间引发一连串的巨大影响。这个概念最初由美国气象学家爱德华·洛伦兹在1963年提出，他在一次演讲中比喻道：“一只南美洲亚马逊河流域热带雨林中的蝴蝶，偶尔扇动几下翅膀，可以在两周以后引起美国得克萨斯州的一场龙卷风。”虽然这个比喻有些夸张，但它很好地说明了事物发展对初始条件具有极为敏感的依赖性，初始条件的极小偏差，也会引起结果的巨大差异。

自洛伦兹首次提出蝴蝶效应以来，这个概念在科学界和公众中都引起了广泛的关注。它被广泛应用于解释各种自然现象和社会现象，如气候变化、金融市场波动、人口增长、传染病传播等。科学家们也在不断探索和研究这个现象的本质和规律，以更好地预测和控制事物的发展。