本文主要是介绍梯度下降法(Gradient Descent),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
梯度下降法(英语:Gradient descent)是一个一阶最优化算法。 要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。如果相反地向梯度正方向迭代进行搜索,则会接近函数的局部极大值点;这个过程则被称为梯度上升法。
- 梯度下降法是最早最简单,也是最为常用的最优化方法。梯度下降法实现简单,当目标函数是凸函数时,梯度下降法的解是全局解。
- 一般情况下,其解不保证是全局最优解,梯度下降法的速度也未必是最快的。梯度下降法的优化思想是用当前位置负梯度方向作为搜索方向,因为该方向为当前位置的最快下降方向,所以也被称为是”最速下降法“。最速下降法越接近目标值,步长越小,前进越慢。
梯度下降法的搜索迭代示意图
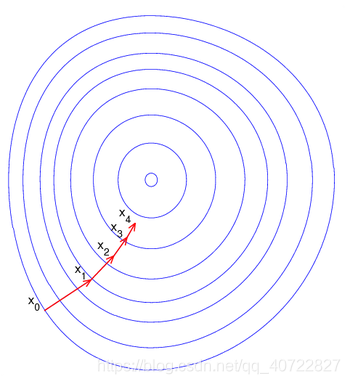
缺点:靠近极小值时收敛速度减慢;直线搜索时可能会产生一些问题;可能会“之字形”地下降。
梯度下降法公式
θ i = θ i − α ∂ ∂ θ i J ( θ 0 , θ 1 . . . , θ n ) \theta_i = \theta_i - \alpha\frac{\partial}{\partial\theta_i}J(\theta_0, \theta_1..., \theta_n) θi=θi−α∂θi∂J(θ0,θ1...,θn)
梯度下降法算法过程:

导数,是对含有一个自变量的函数进行求导。
偏导数,是对含有两个自变量的函数中的一个自变量求导。
你知道的越多,你不知道的越多。
有道无术,术尚可求,有术无道,止于术。
如有其它问题,欢迎大家留言,我们一起讨论,一起学习,一起进步
这篇关于梯度下降法(Gradient Descent)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






