【深蓝学院】移动机器人运动规划--第3章基于采样的路径规划--笔记

本文主要是介绍【深蓝学院】移动机器人运动规划--第3章基于采样的路径规划--笔记，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

0. Preliminaries

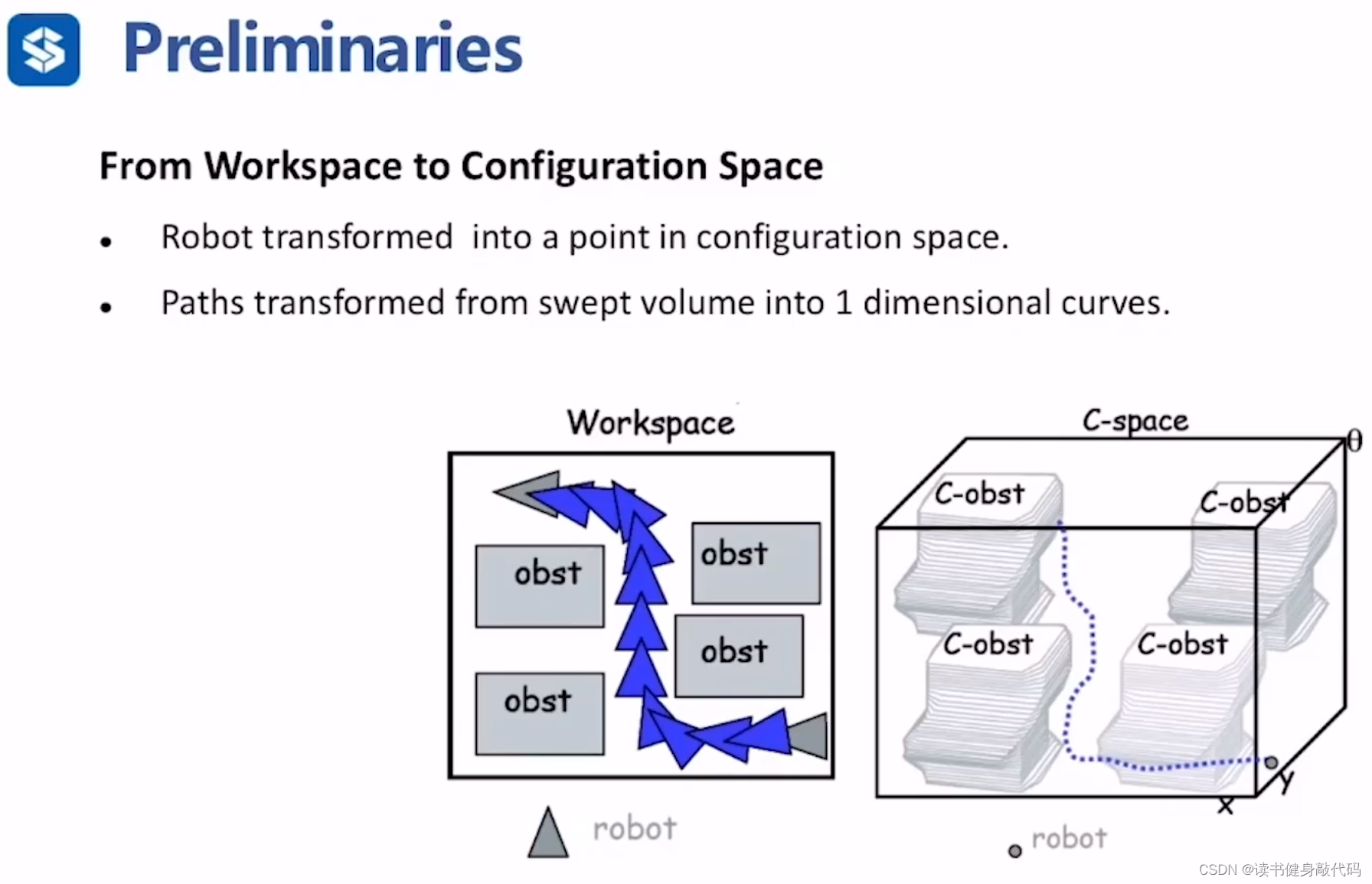
在这里插入图片描述
做规划都是将WS转到C space下进行。

在这里插入图片描述
找到可行解和最优解（这两个不同）
通过增量或者批次地在C-space中采样来增量式地构建树或者图。
不显式地构造

如果把整个规划问题看成一个大的优化问题，那么大问题可以拆分成小问题进行求解。

在这里插入图片描述
整个规划问题可以分为两个基本的tasks：Explotration和Exploitation
Explotration目的是获取搜索空间中的拓扑信息，即尽可能地把树给更多地长出来
Exploitation目的是使用Explotration过程中获得的信息来增量式地优化解，即优化树的拓扑结构。

在这里插入图片描述
Probabilistic Completeness概率完备：是对可行解而言，即如果一个解是可行的，则我们随着我们采样的进行，我们一定能够找到它。
Asymptotical Optimality渐进最优：针对最优解而言，随着采样的次数趋近于无穷为，我们找到最优解的概率会趋近于1
即时性Anytime：我们能够很快地找到可行解(但)，随着计算资源的投入我们能够找到更优的解。

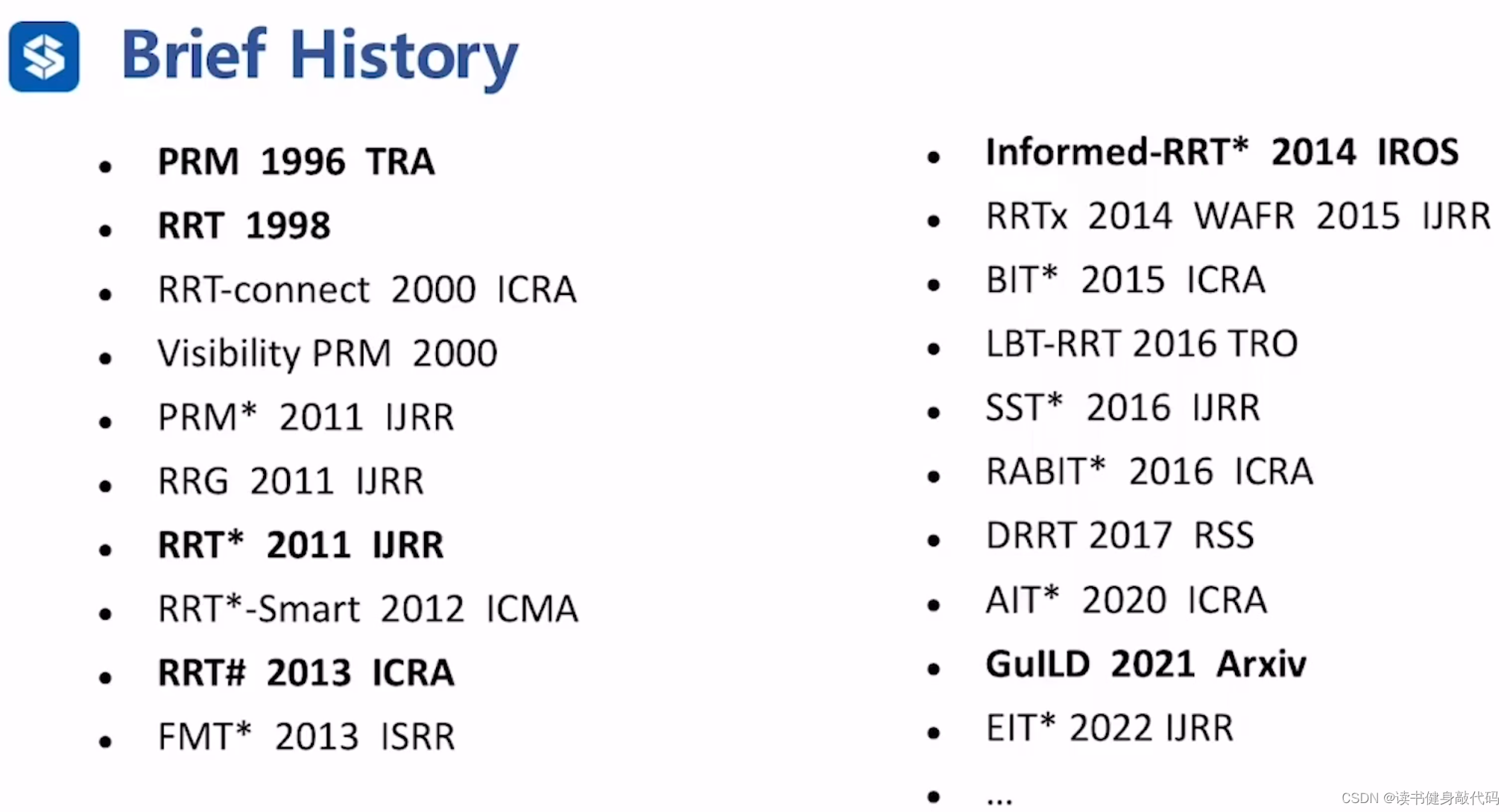
在这里插入图片描述
采样类算法的发展时间，和给予搜索的规划算法不同，采样类算法是近20年才发展起来的（有些令人惊讶），而如A*这类算法是上世纪50，60年代发展的。

本章内容：
在这里插入图片描述
分别讲可行解，最优解，加速收敛的算法(很多都是基于RRT*发展而来)。

1. Feasiable path planning methods

1. PRM(概率路线图)

1.1.1 PRM

PRM是一种概率完备（probabilistically complete）的算法，意味着随着采样数量的增加，找到一条路径（如果存在的话）的概率趋近于1。然而，它并不保证找到的是最优路径，也不是确定完备的，即它不保证总是在有限的时间内找到解决方案。
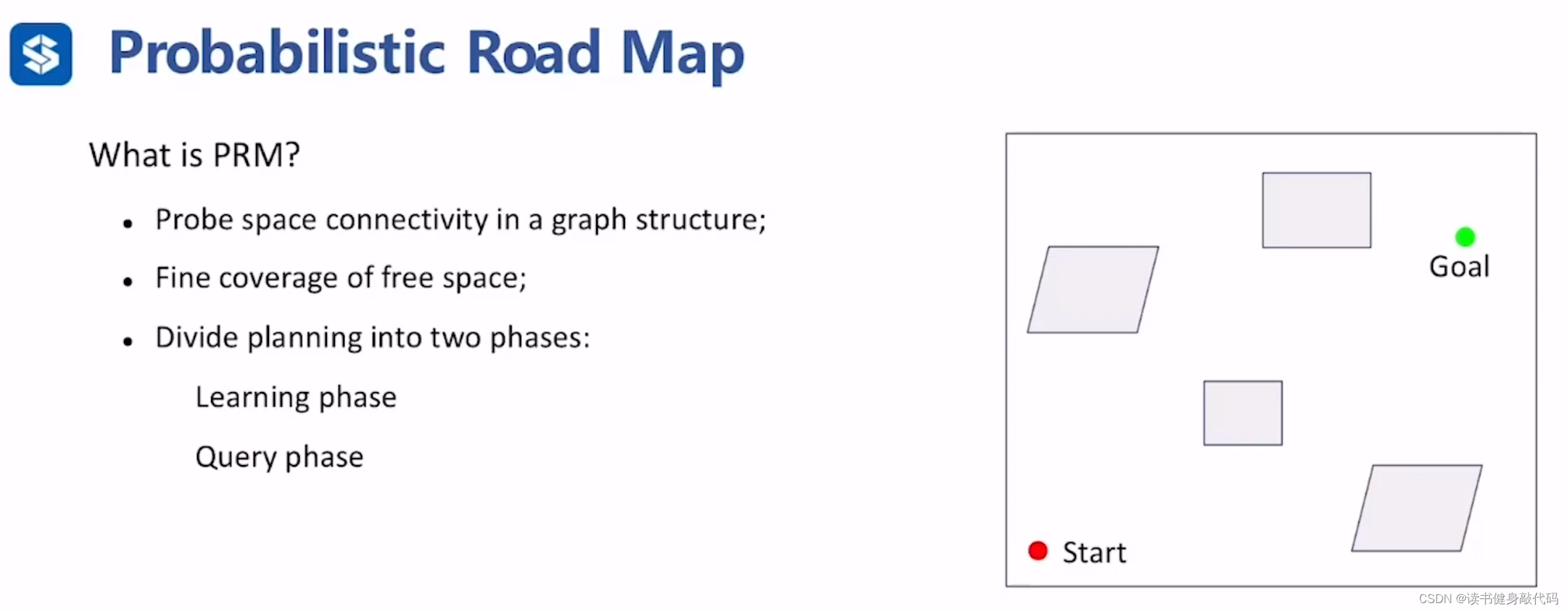
在这里插入图片描述
得到一个图的结构来探索解空间的连续性；
希望很好地去覆盖解空间；
分为两个阶段：learning phase（构建图的过程），query phase（在图的基础上进行搜索得到解）

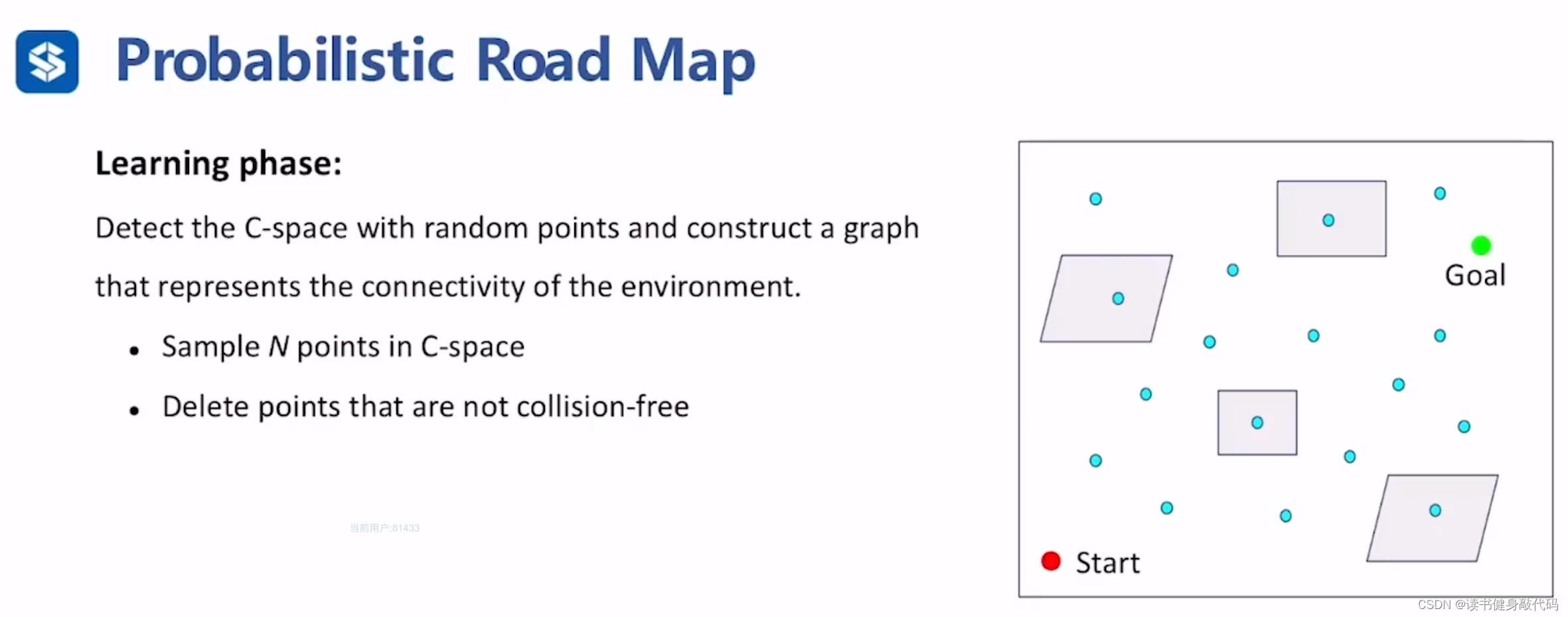
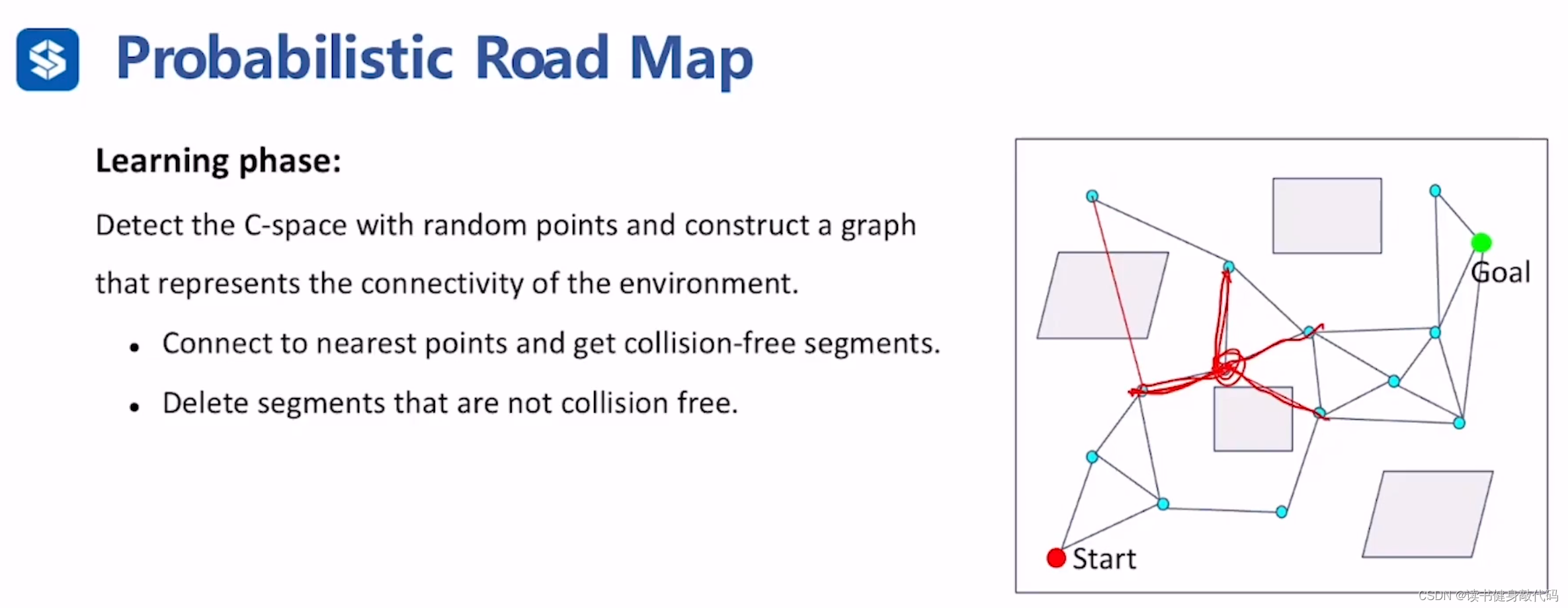
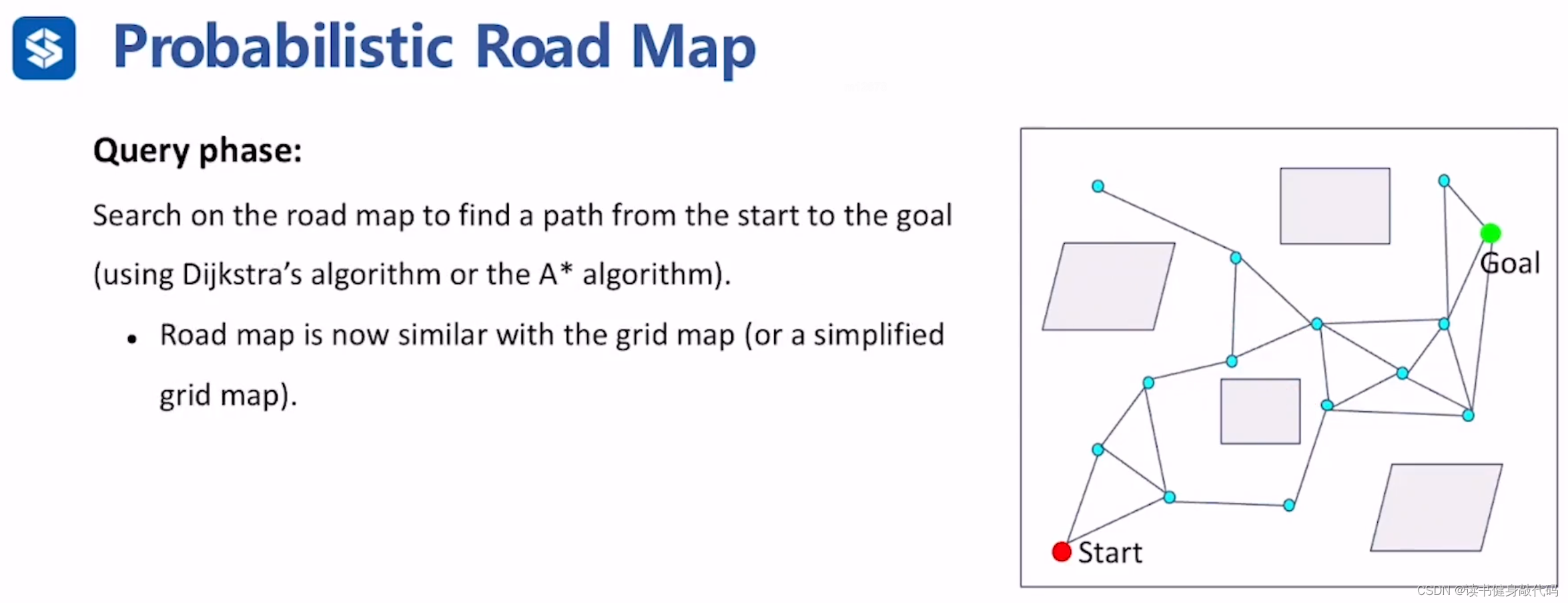
在这里插入图片描述

Learning phase

在C-space中采样，得到一系列采样点，
对采样点进行碰撞检测，delete not collision-free的点，保留collision-free的点
找到留下的采样点的领域内的neighbor node，进行连接
去掉连接边not collision-free的边

Learning phase结束，得到表征C-Space连通性的、collision-free的图结构，进入query phase，有了图之后就可以使用之前的A*或者Dijkstra来进行搜索了。

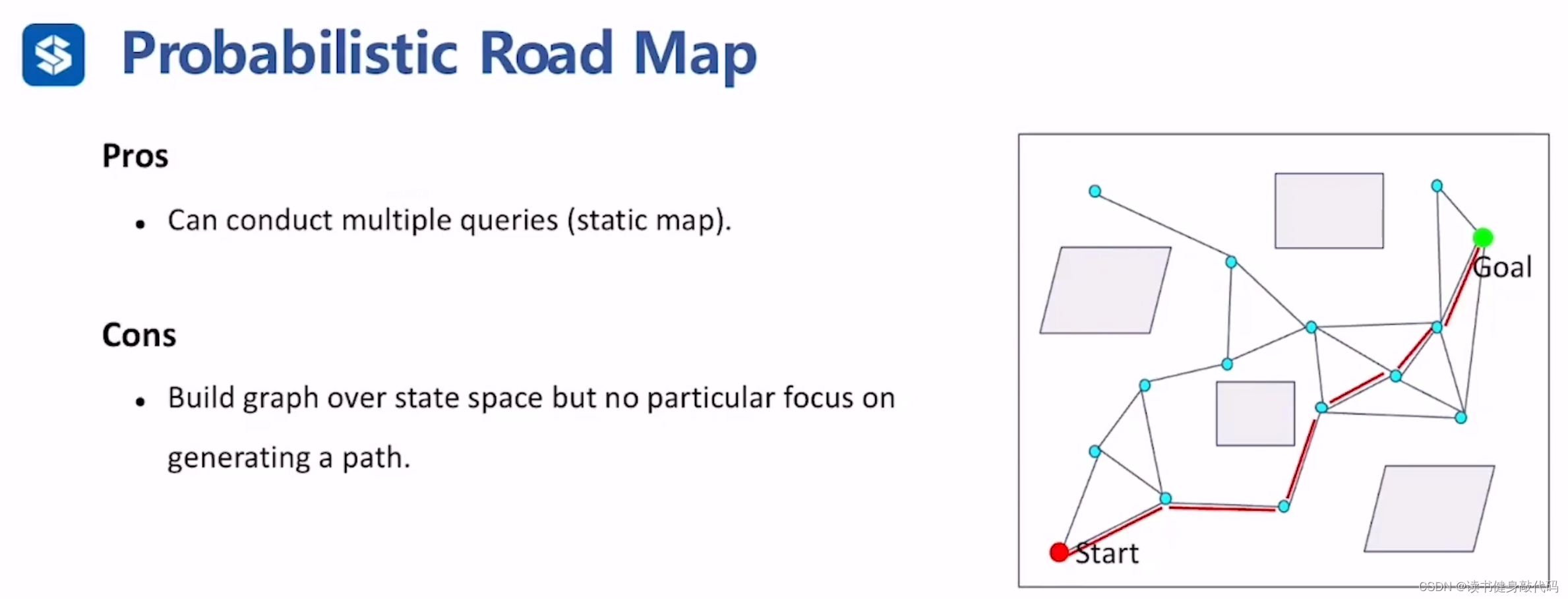
在这里插入图片描述

优点：由于是静态地图，所以可以进行multiple queries（multiple queries是什么？在什么情况下会使用？）
缺点：基于状态空间建图，不focus on生成某一条特定的path（且环境可能会发生变化，我们有时候只希望找到某条特定解，而不是希望得到整个state space的空间连通性的图，也就是效率低，RRT对此进行了改进）。

1.1.2 Lazy collision-checking

基于以上分析，频繁地进行collision query非常耗时，所以提出了改进Lazy collision-checking(check collision only if necessary)
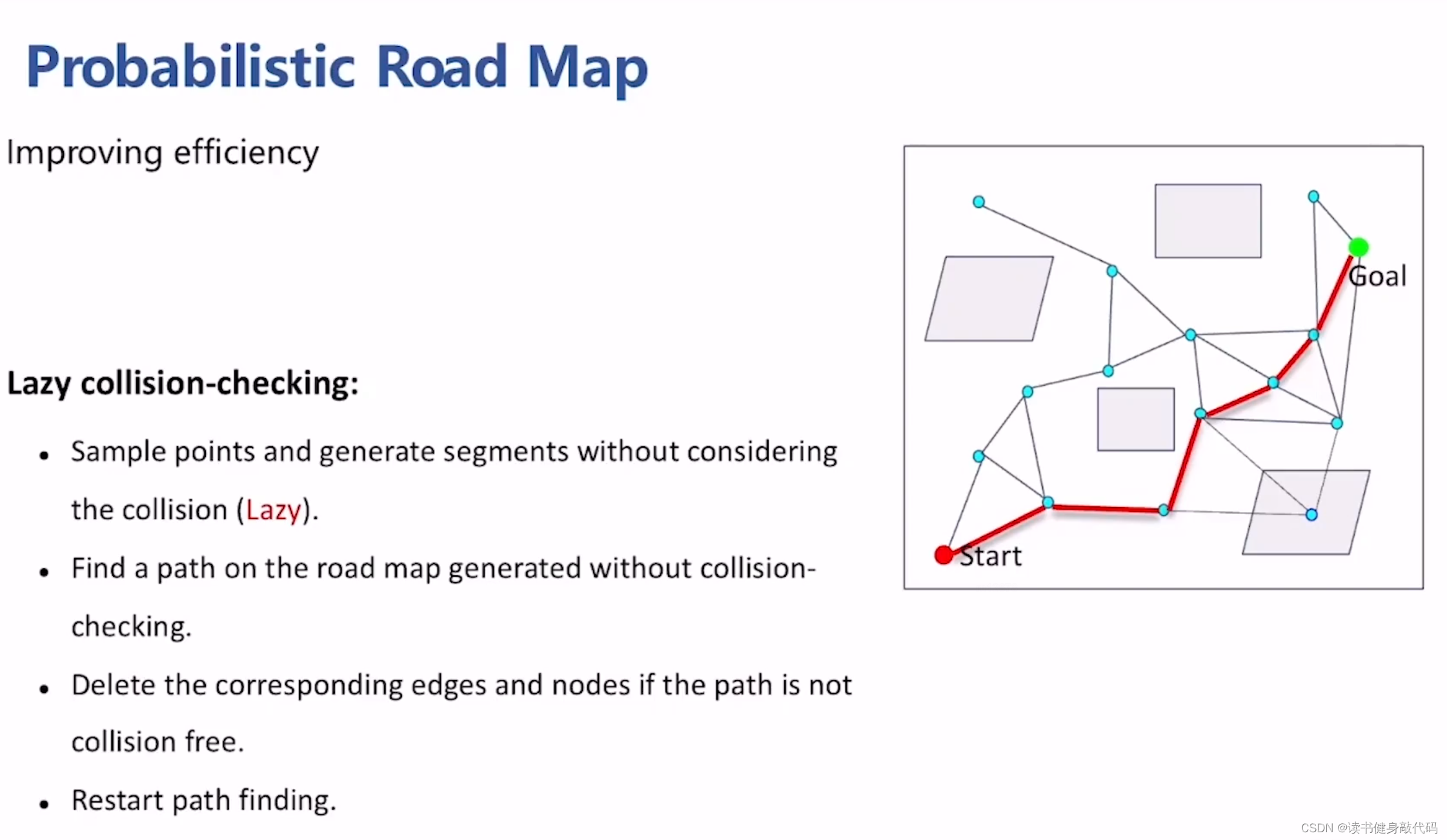
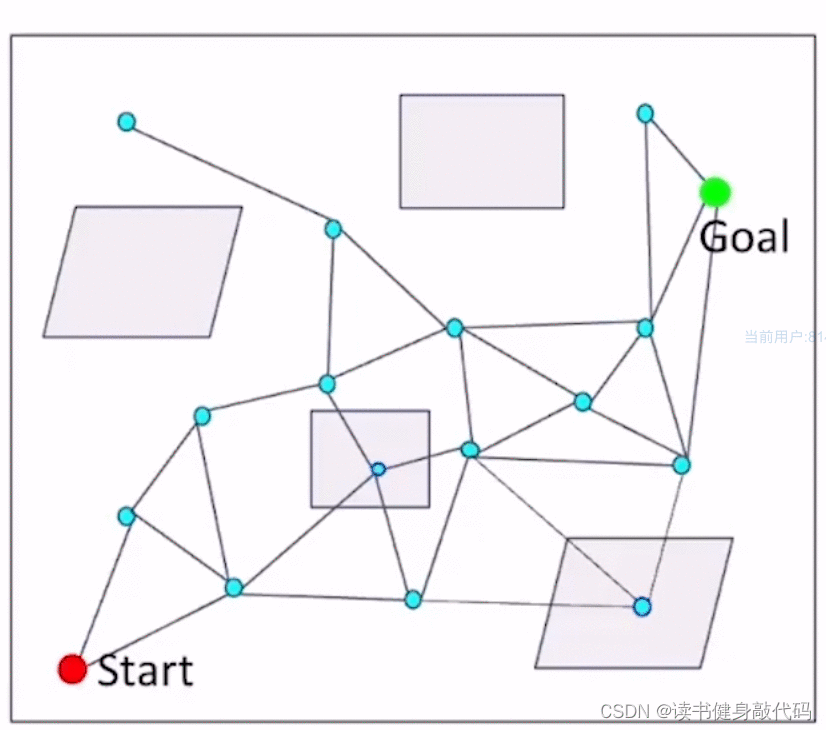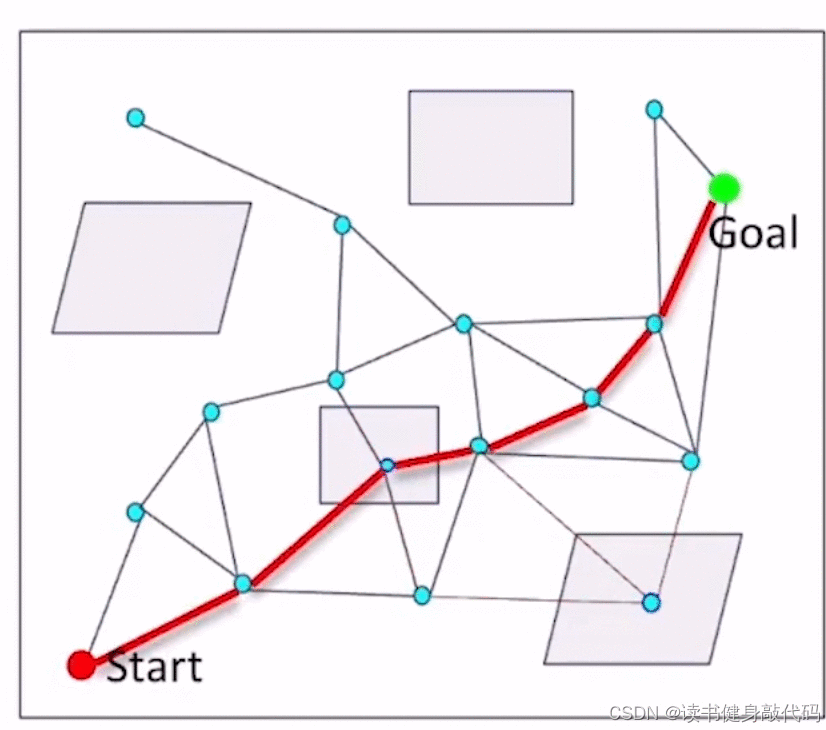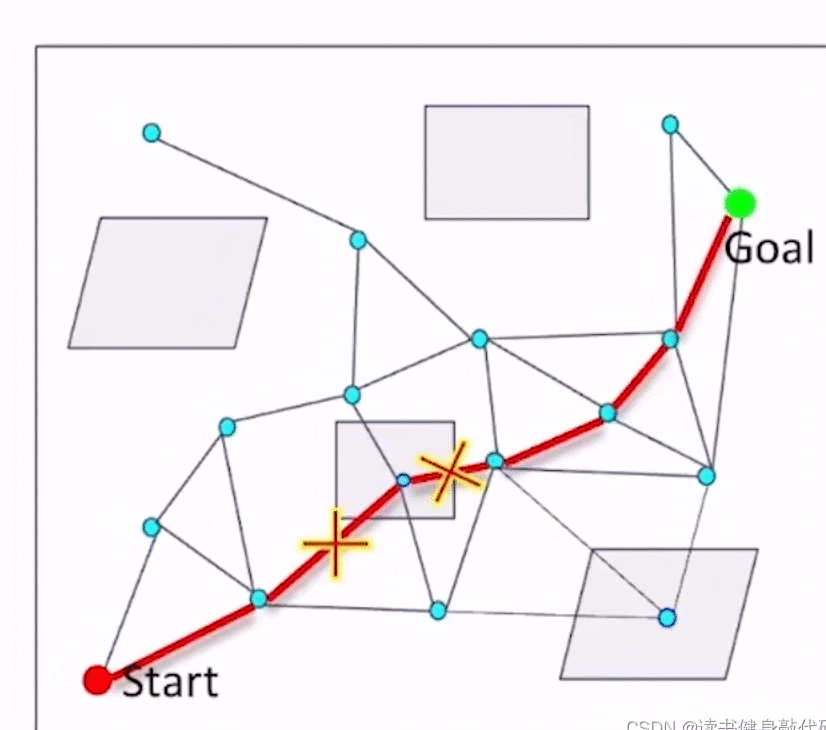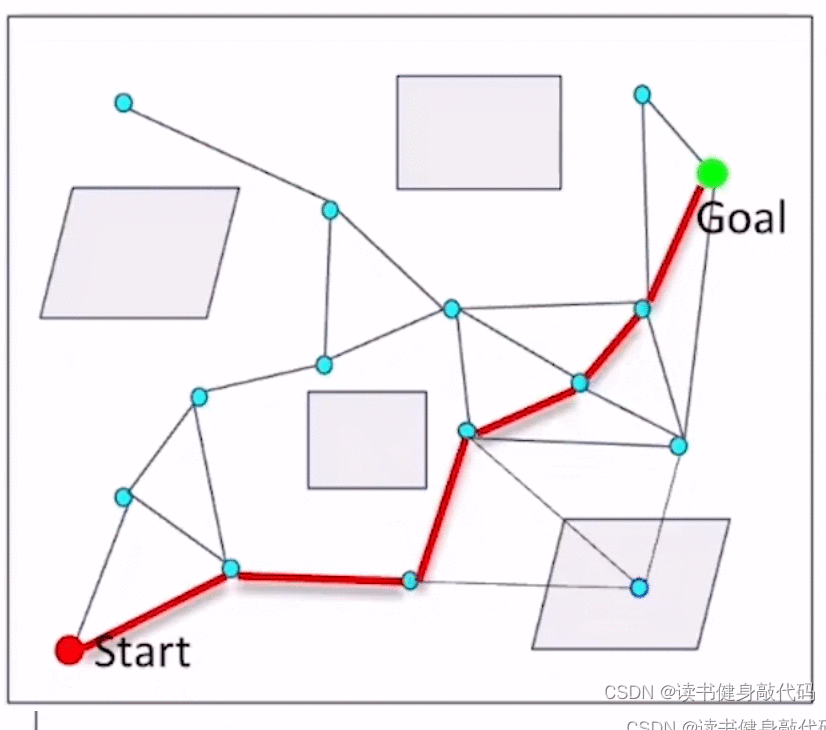
在这里插入图片描述

在这里插入图片描述
基本思想：

采样
连接边，但不对边进行check collision
在边中找到一条path，
对这条path进行collision checking，去掉collision的边，
在图上再搜索一条path，重复step4，知道找到一条collision-free的path。

1.2 RRT(快速搜索随机树)

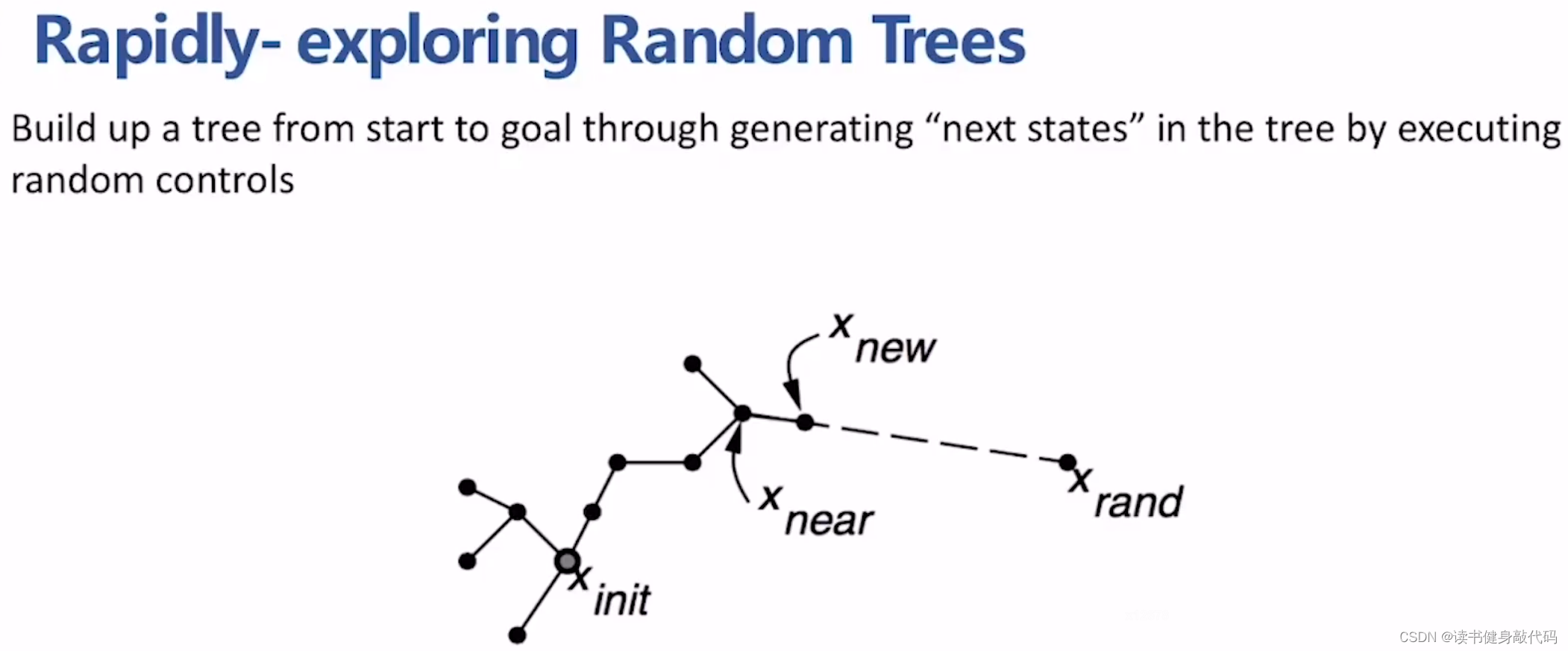
在这里插入图片描述
不同于PRM的multi query，RRT是向目标点的方向长出一棵树。

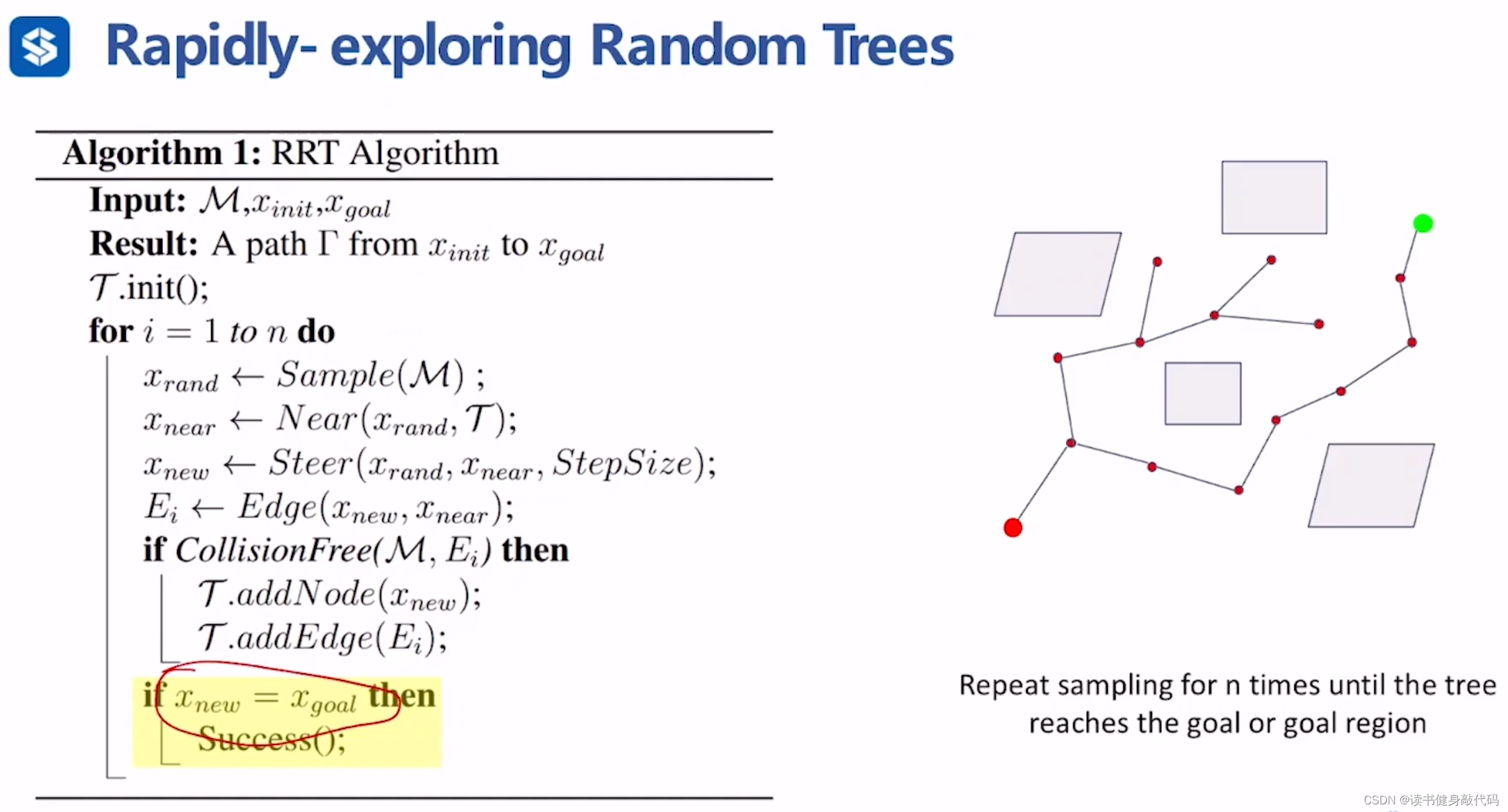
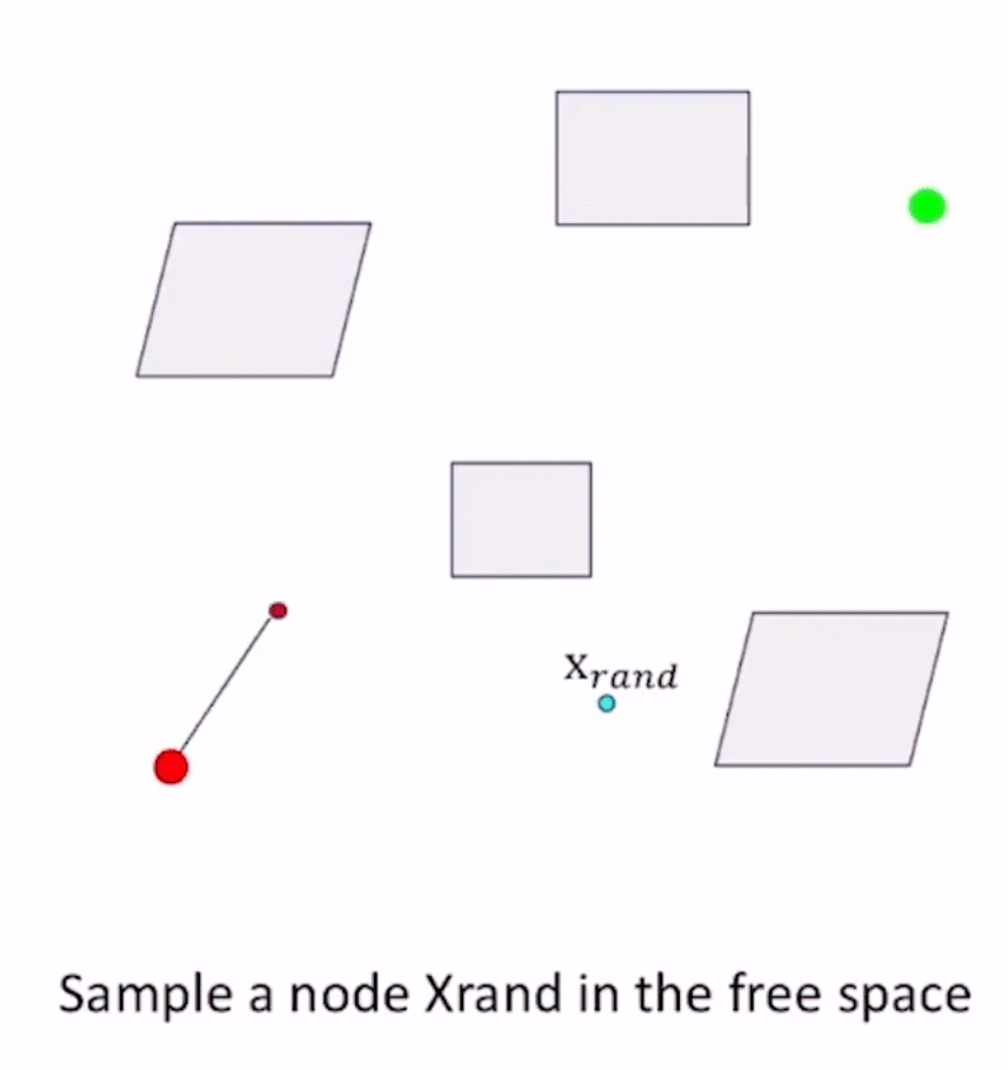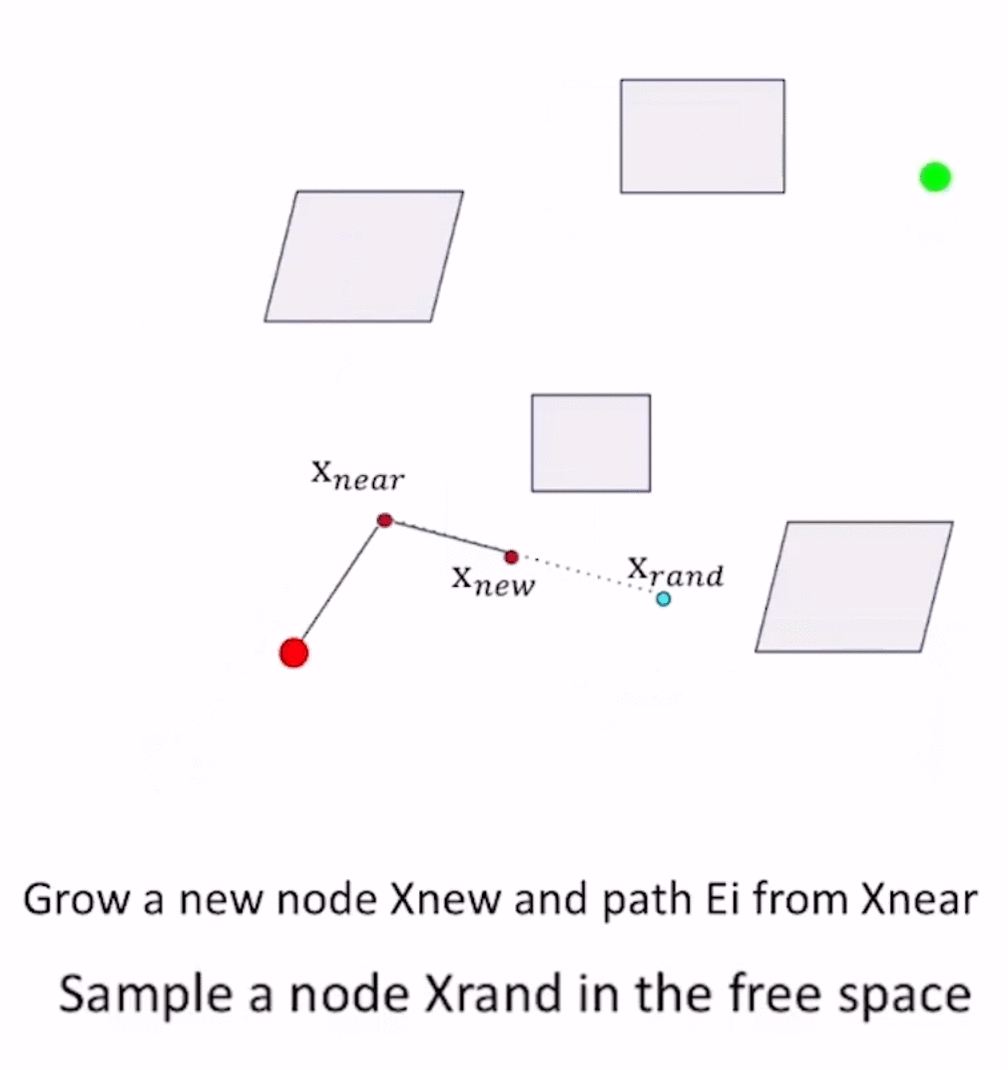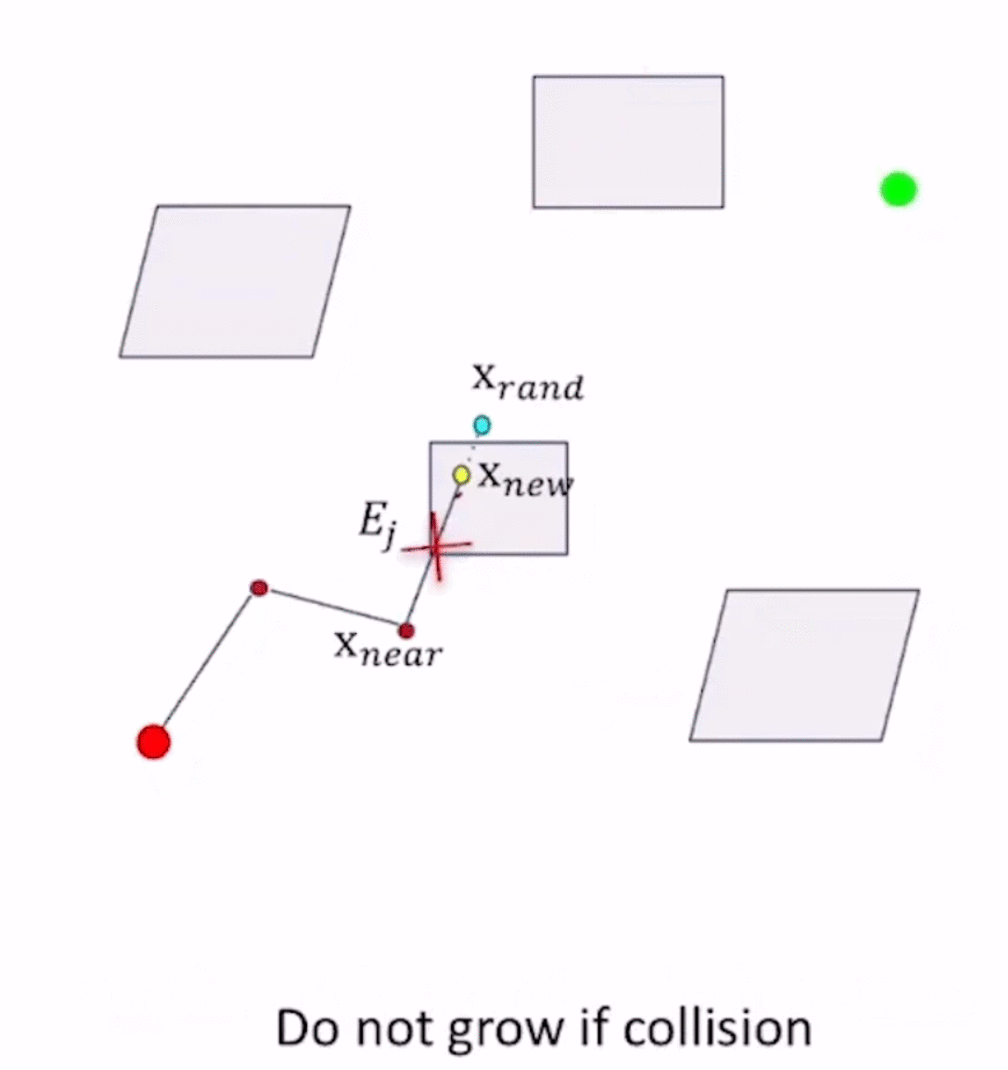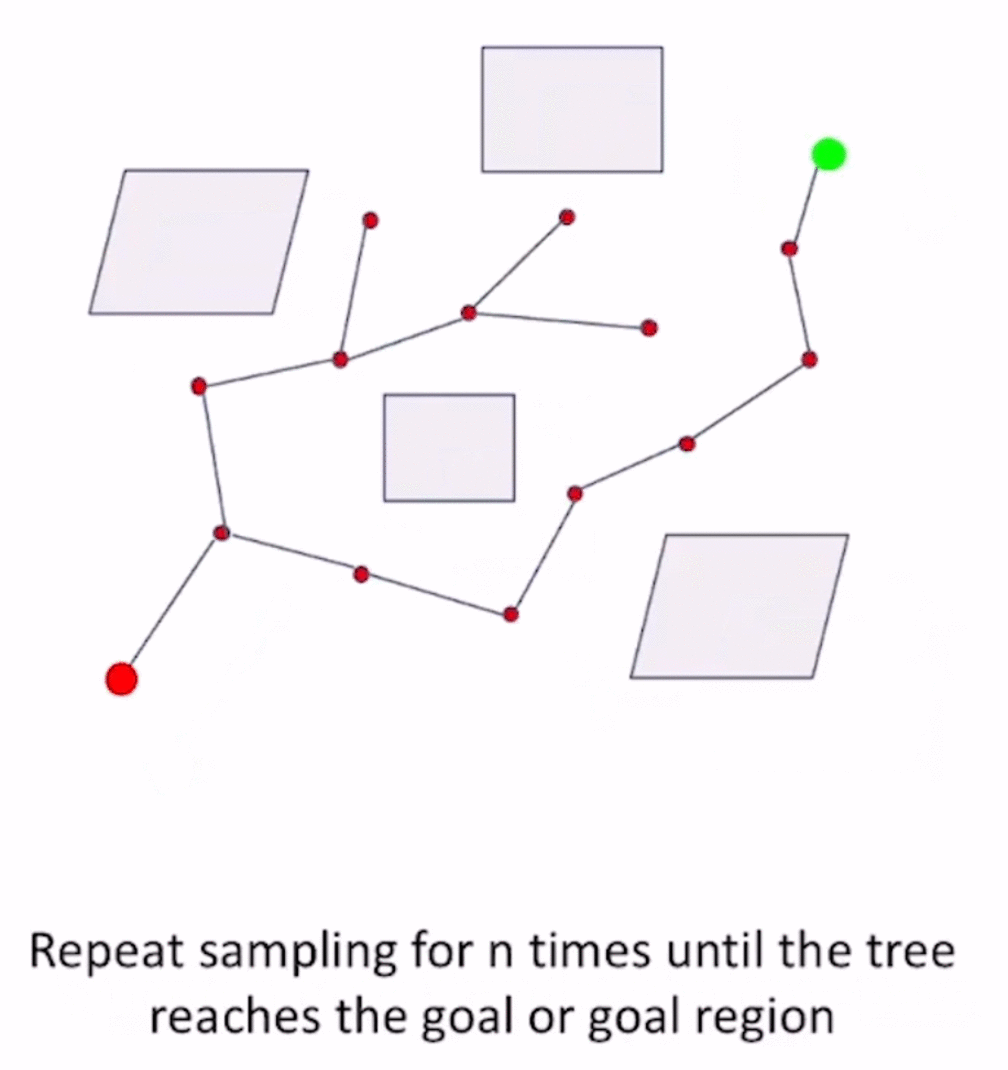
在这里插入图片描述

算法流程

从起点开始sample，得到collision free的 $x_{near}$
以 $x_{near}$ 为起点，往一个方向采样得到 $x_{near}\to x_{rand}$ 方向，在这个方向上取 $St e pS i ze$ 的边，进行collision checking：

如果是collision-free的，则采用 $x_{near}\to x_{rand}$ 这条边，更新， $x_{new}=x_{near} + \bm{StepSize}$
如果发生collsion则在 $x_{near}$ 基础上重新sample获得 $x_{rand}$
循环step2，直到找到 $x_{goal}$ ，找到条件 for example， $x_{near}$ 距离 $x_{goal}$ 小于某个阈值，则认为找到了 $x_{goal}$ 。

可以用ZJU-FAST-LAB的这个工作来仿真：https://github.com/ZJU-FAST-Lab/sampling-based-path-finding
里面的代码有些旧的地方需要改一下才能编过，要改的地方不多，比如把boost::shared_ptr改成std::shared_ptr等。

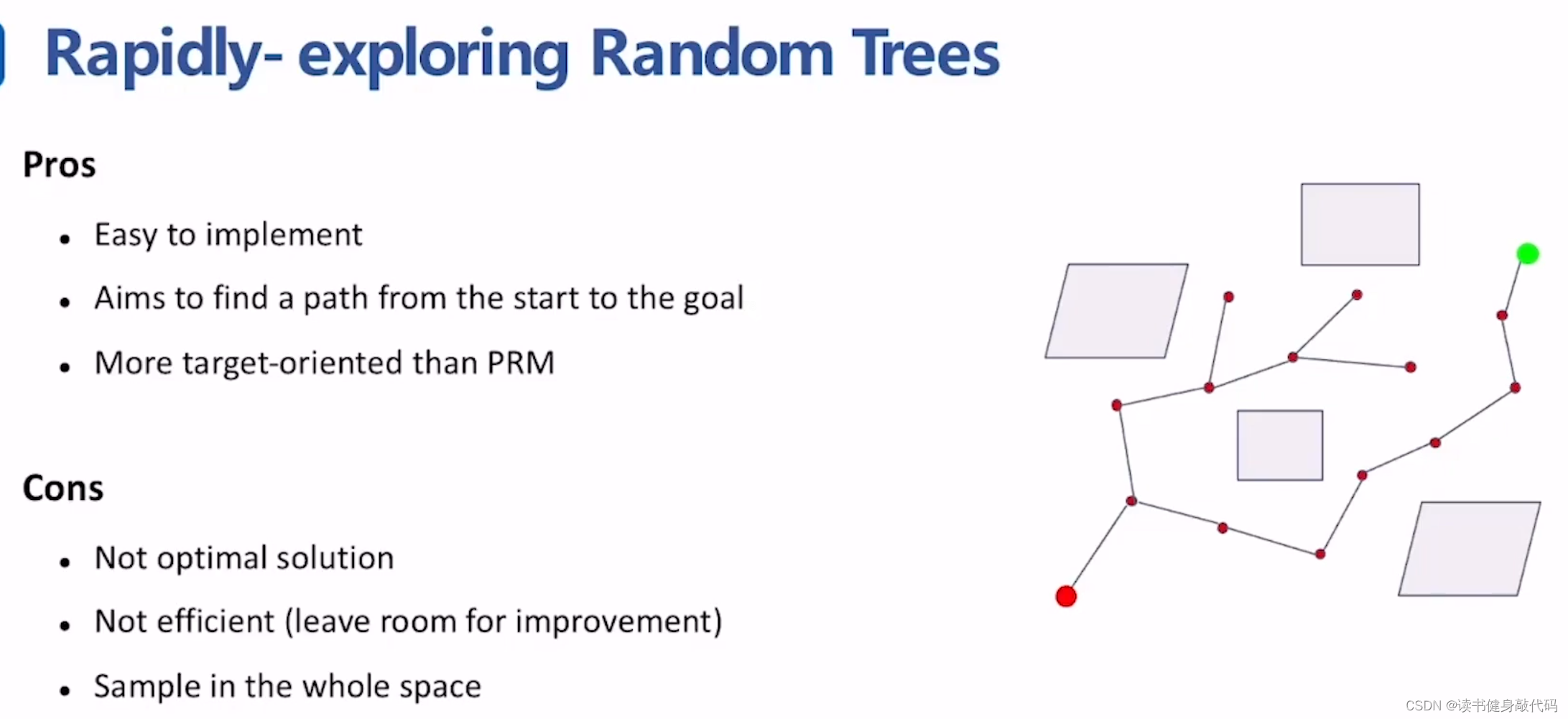
在这里插入图片描述
优点：简单易实现，比PRM更target-oriented，更优目的性，而不是构建全图。
缺点：是可行解，但不是最优解，不够高效（可以从sample方式，搜索算法方面改进）。

2. Optimal path planning methods

2.1 Optimal Criterion(最优性准则)

贝尔曼动态规划最优性准则的离散形式：
在这里插入图片描述

j的cost=min(j的前驱节点的cost(不止一个)+ij间的cost)
f(i)继续往前回溯，直到回溯到start节点。
以上为准则，不是算法。

在这里插入图片描述
直接动态规划方法(DDP，Direct Dynamic Programming)，在某些情况下假定图是无环的，但这种假设通常与问题的特定类别或应用场景相关，而不是与DDP方法本身固有相关。

DDP具体步骤

初始化任意两个节点的cost-to-come valu为 $\infty$ ，即表示 $i, j$ 间不存在路径，距离保持无穷大，这两个点之间不可达。
使用贝尔曼动态规划最优性准则进行迭代。

其中"cost-to-come" 值(即f值)表示从起始点到达当前点所需的代价。在机器人路径规划问题中，“cost-to-come” 可能代表机器人从起点移动到当前位置所需的最小能量。通常与 “cost-to-go” 或 “cost-to-arrive” 结合使用，该值表示估计从当前状态到达目标状态的预期代价。

DDP讨论：
例如，在某些任务规划或决策问题中，要求图是无环的，是为了保证每个决策或状态转移都是向前的，即从一个状态转移到另一个状态不会回到之前的状态。这可以确保算法总是向目标状态前进，而不是在某些状态之间无限循环，这样就可以在有限的步骤内找到最优解。

在无环图（如有向无环图，简称DAG）上应用动态规划的另一个原因是，无环图有一个自然的拓扑排序。这意味着可以按照一定的线性顺序处理所有节点，使得在计算当前节点的最优值之前，所有前置节点的最优值已经被计算。这为动态规划方法提供了一个明确的结构，以便按顺序解决子问题，并最终得到全局的最优解。

在具体实践中，如果我们面对的是一个有环图，那么动态规划问题可能会变得更加复杂，因为可能存在回路，这意味着某个状态可能会重复出现，从而可能导致无限循环。在这种情况下，我们可能需要额外的策略来处理环，例如设置状态访问的限制，或者使用其他算法如贝尔曼-福特算法，它可以处理有向图中的负权重边，但同时也能检测到负权重环。

当假设图是无环（acyclic，即层级结构），每个状态(每个节点的state)仅使用一次最优准则即可算出，也即在计算新节点的cost-to-come value时，该节点的前驱节点的cost-to-come value已被算出。

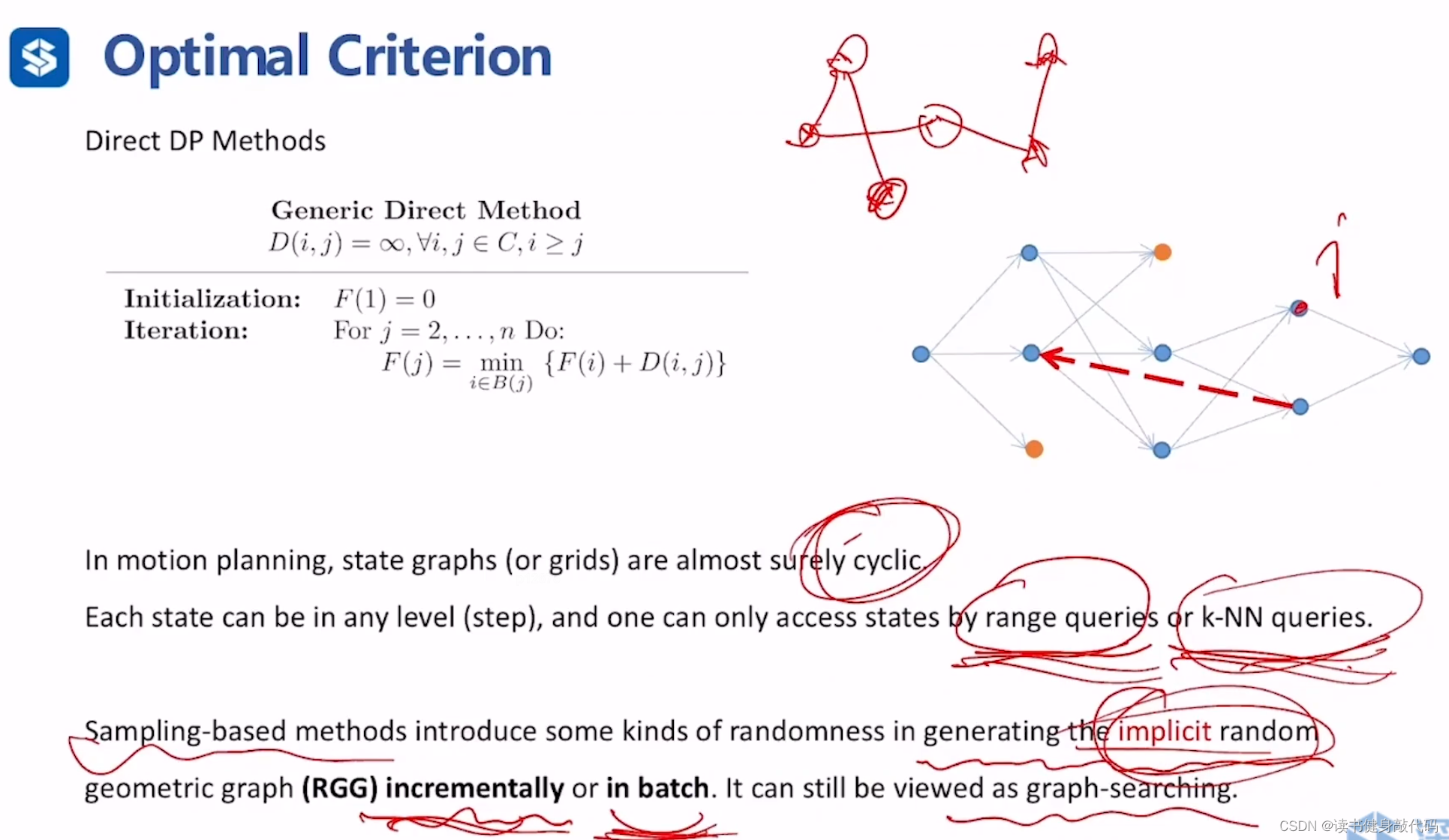
在这里插入图片描述

在实际的机器人运动规划中，几乎state graphs(or grids)总是存在环结构，而且我们对于state的访问也不是层级式的访问，而是range queries或k-NN(对临近节点)的访问。

sampling-based methods和graph search based methods的不同在于：前者是在生成的隐式随机几何图(RGG,implicit random geometric graph)上进行，构建图的方法存在随机性，且是增量或者批量(batch)的构建的，后者是在确定的图上进行的，图的构建通常是先全部完成。
所以本质上，sampling-based methods也可以看做图搜索方法。
（这段可以学完之后再来看看视频）

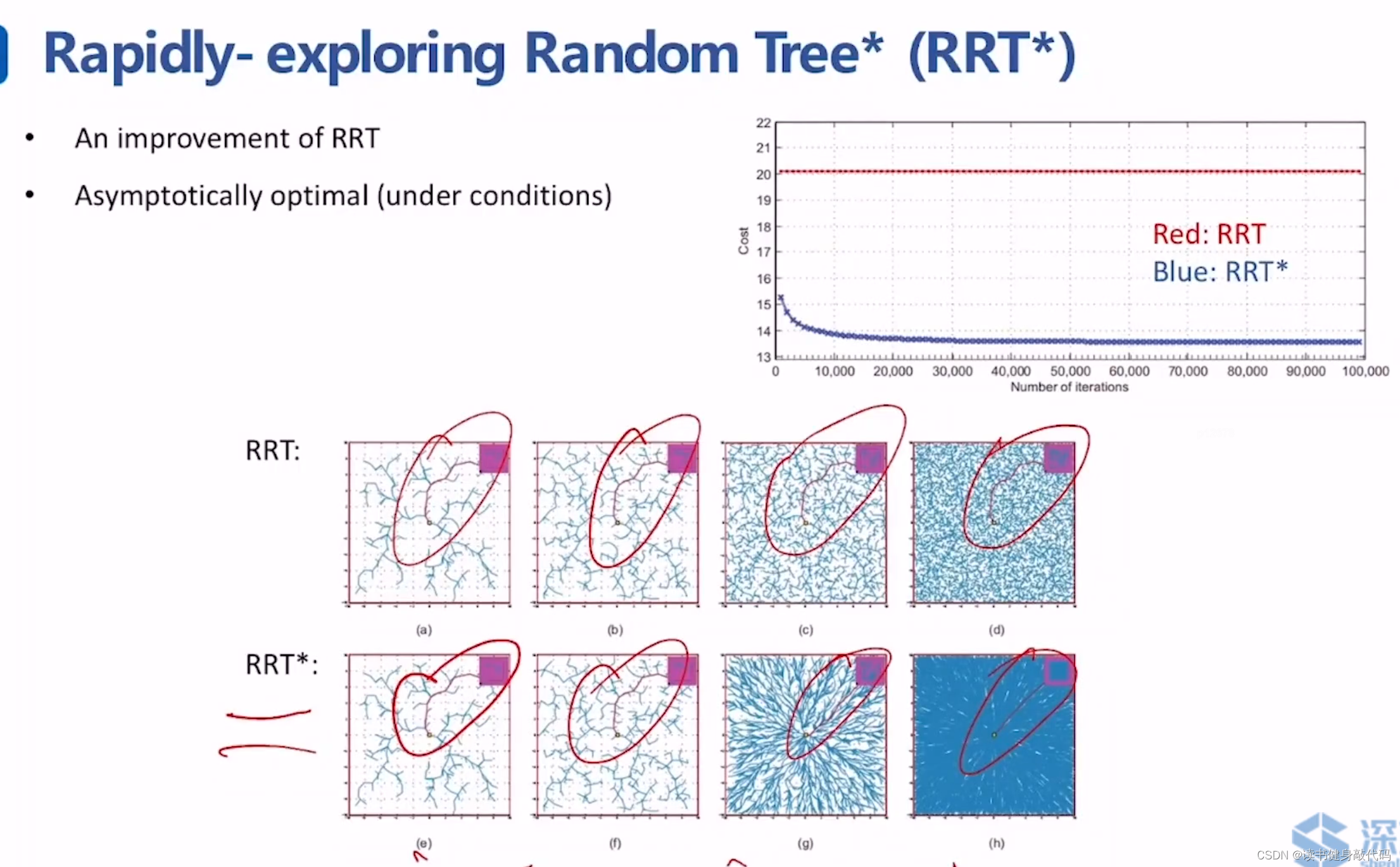
在这里插入图片描述

2.2 RRT*

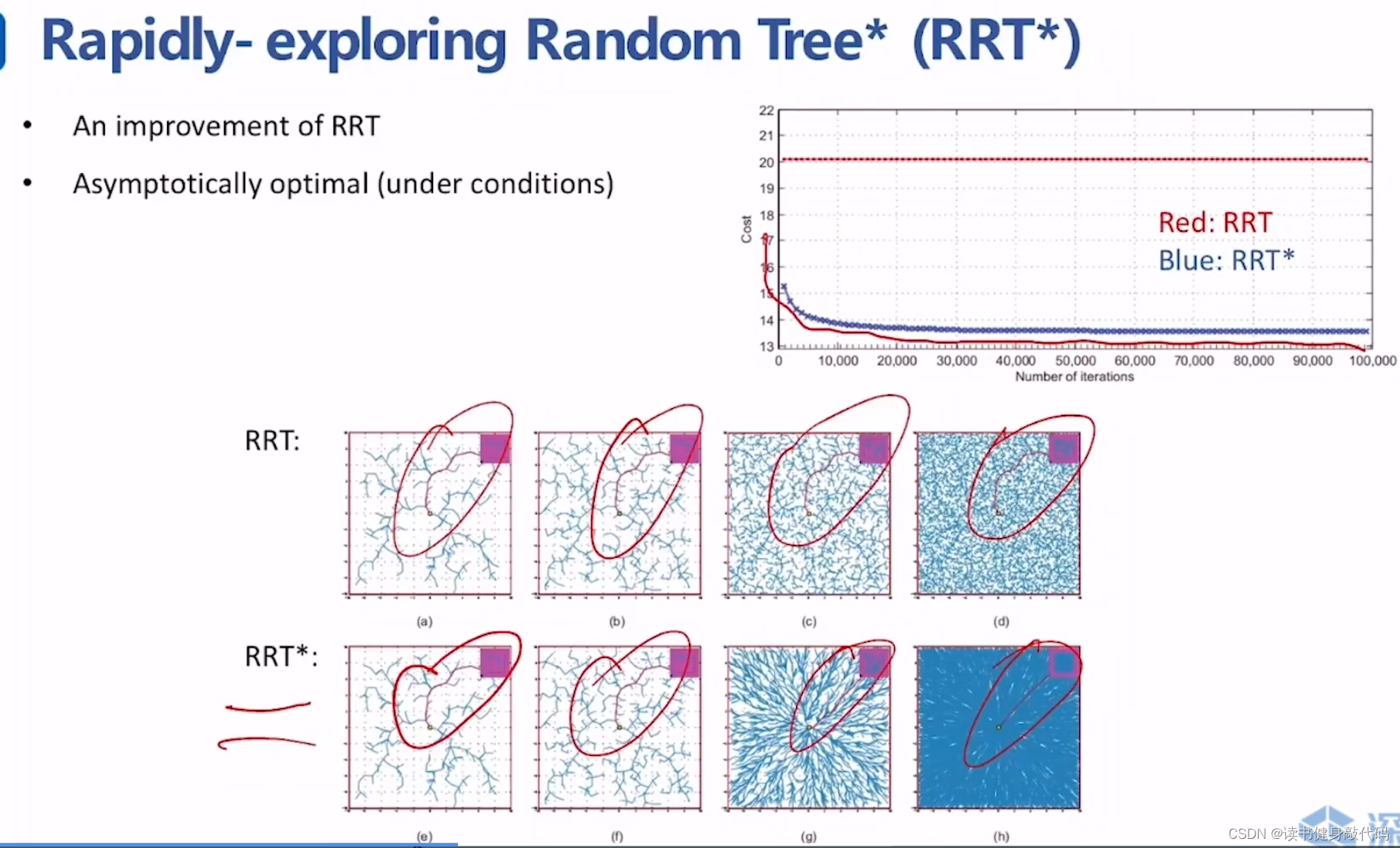
在这里插入图片描述
RRT* $^{[1]}$ 在运行过程中的解是被不断优化的，解是渐进最优的。

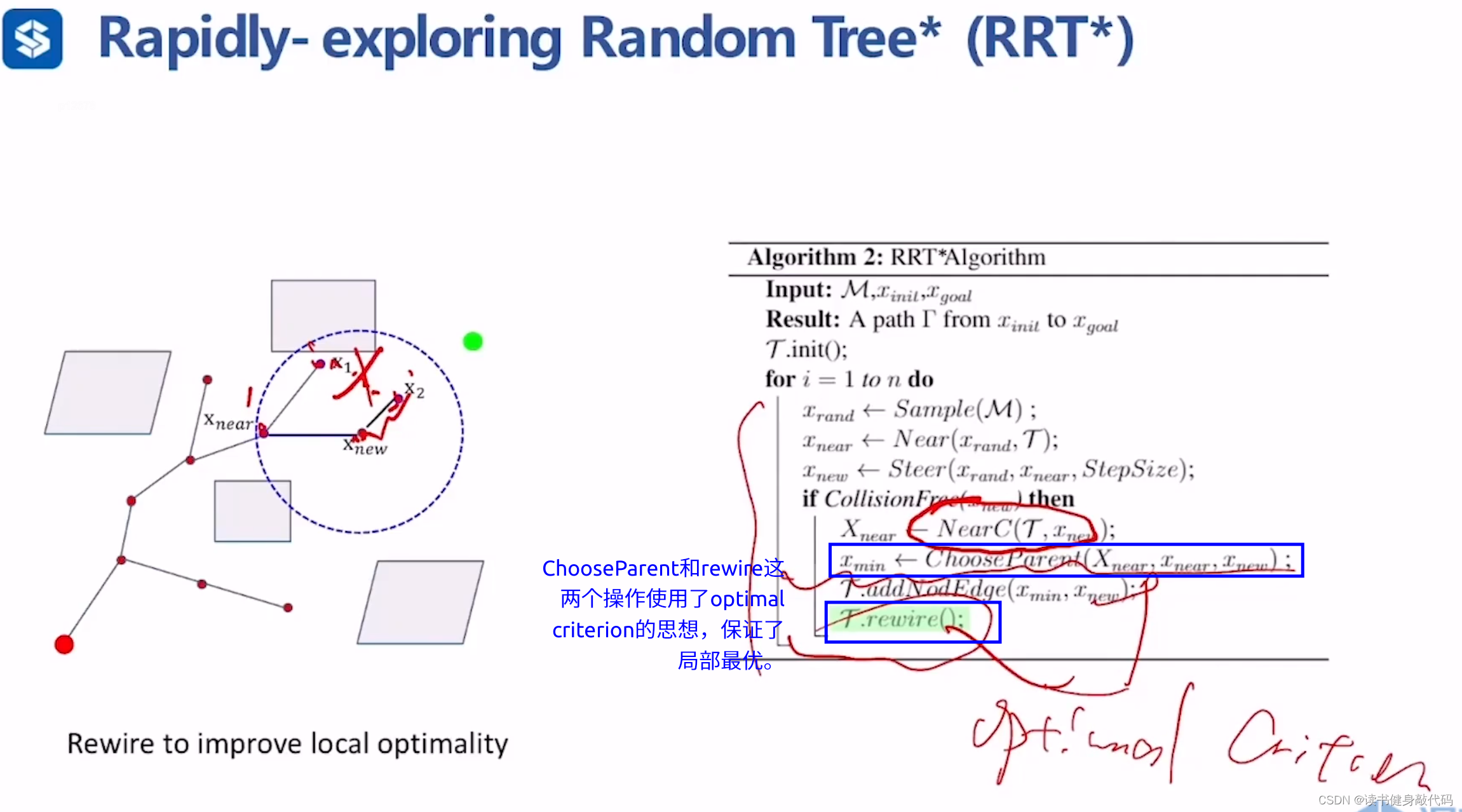
在这里插入图片描述

在这里插入图片描述
RRT*相较于RRT，使用了Optimal Criterion，体现在ChooseParent和rewire（重连）两个函数上。

RRT*流程如下：

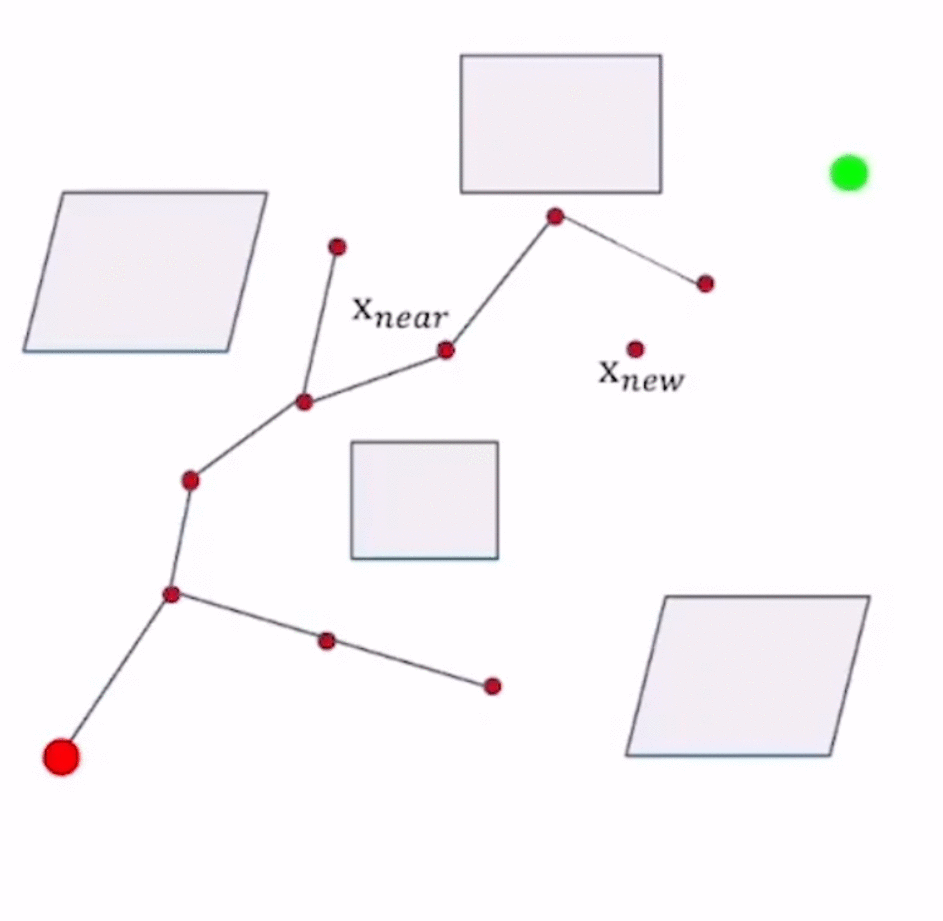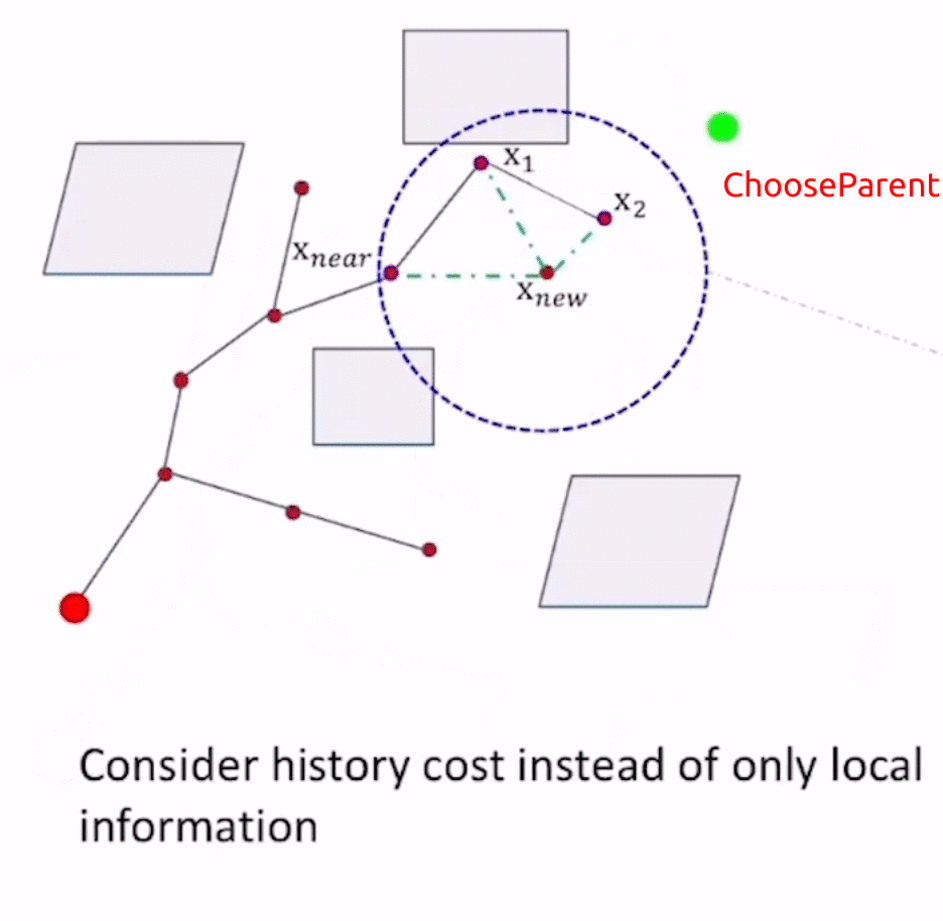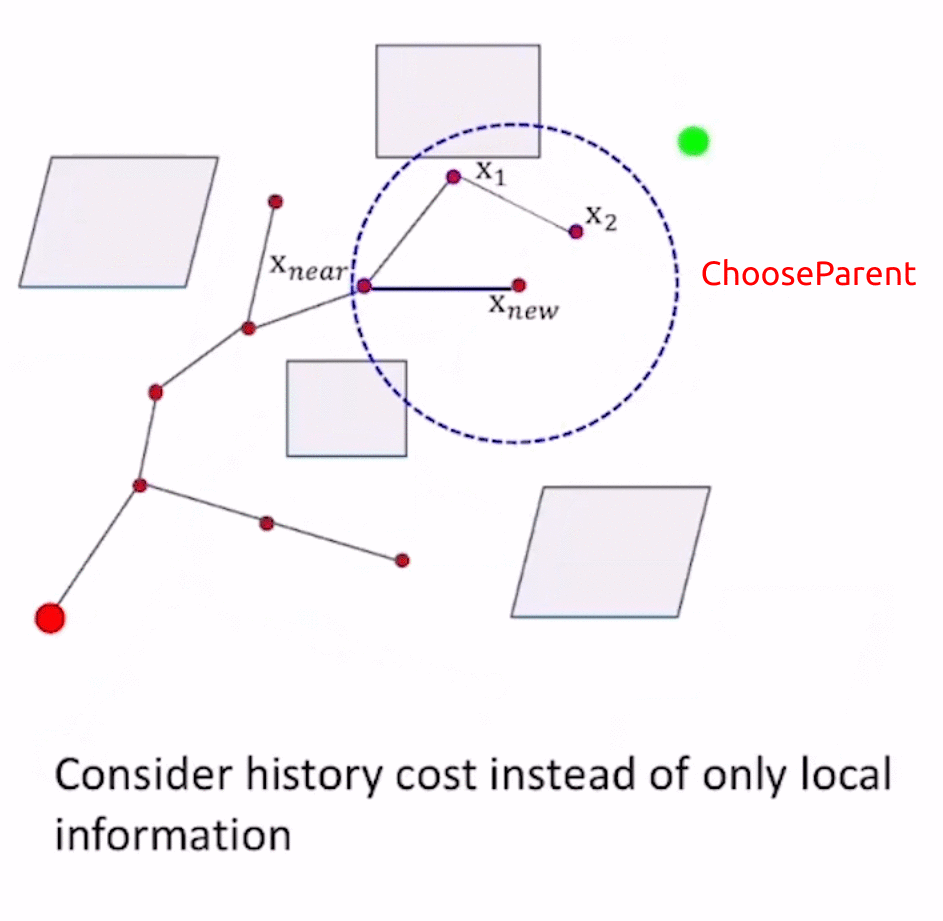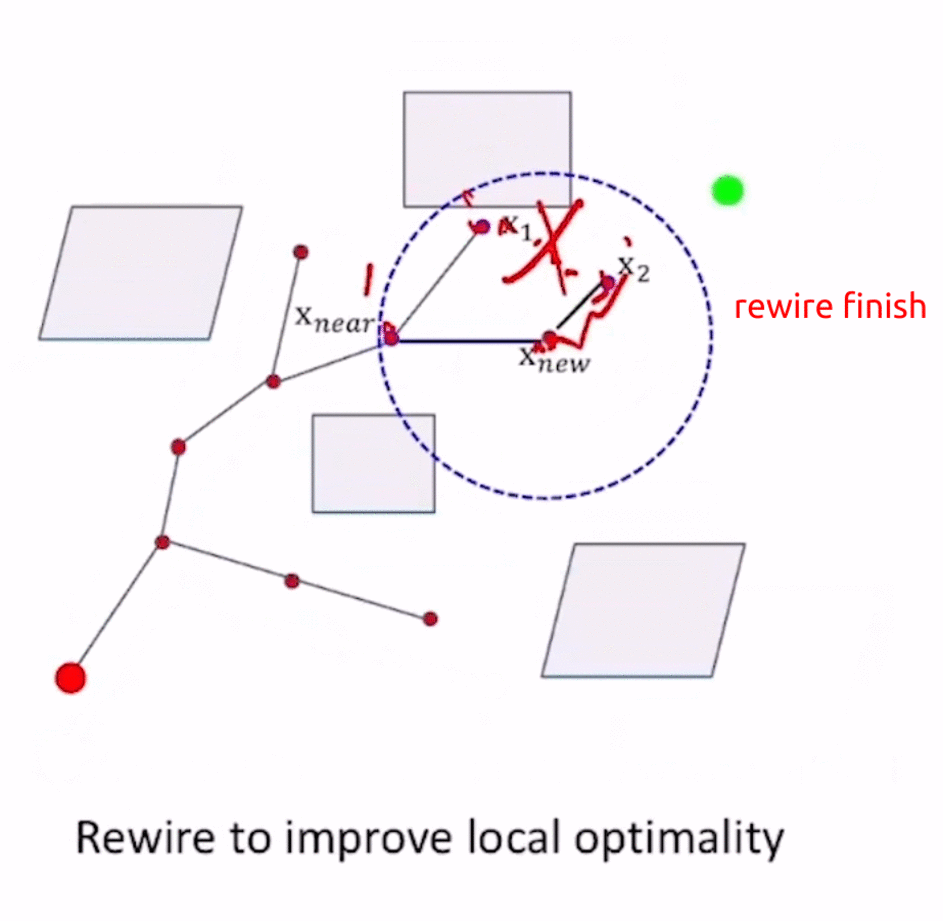
上例中，起始阶段已经从 $x_2$ 采样得到了 $x_{new}$ 的位置，接下来要对 $x_{new}$ 进行决策。
RRT*中sample选取 $x_{new}$ 的方式与RRT相同，在获得 $x_{new}$ 之后，

RRT直接取 $x_{new}$ 作为新的路径点，
而RRT*使用Optimal Criterion的思想进行了ChooseParent，以 $x_{new}$ 为圆心、query range为半径的圆的范围内检测新路径点的candidates(即图中的 $x_{near},x_1,x_2$ )，以各个candidates作为 $x_{new}$ 的前驱节点，计算 $x_{new}$ 的cost-to-come值(即f值)，选取f值最小的前驱节点 $x_{near}$ 作为 $x_{new}$ 的父节点，增加父节点到子节点的边 $Edge_{x_{near}\to x_{new}}$ 。

对 $x_{new}$ 的其他parent candidates进行rewire，若从 $x_{new}$ 到达该candidate时的f值更小，则增加 $Edge_{x_{new}\to x_{candidate}}$ ，删除原来的 $Edge_{x_{else\_node}\to x_{candidate}}$ (类似于Dijkstra中的更新节点cost值为更小的)。

通过ChooseParent和rewire操作，使得RRT*在不断地采样过程中不断接近最优路径。

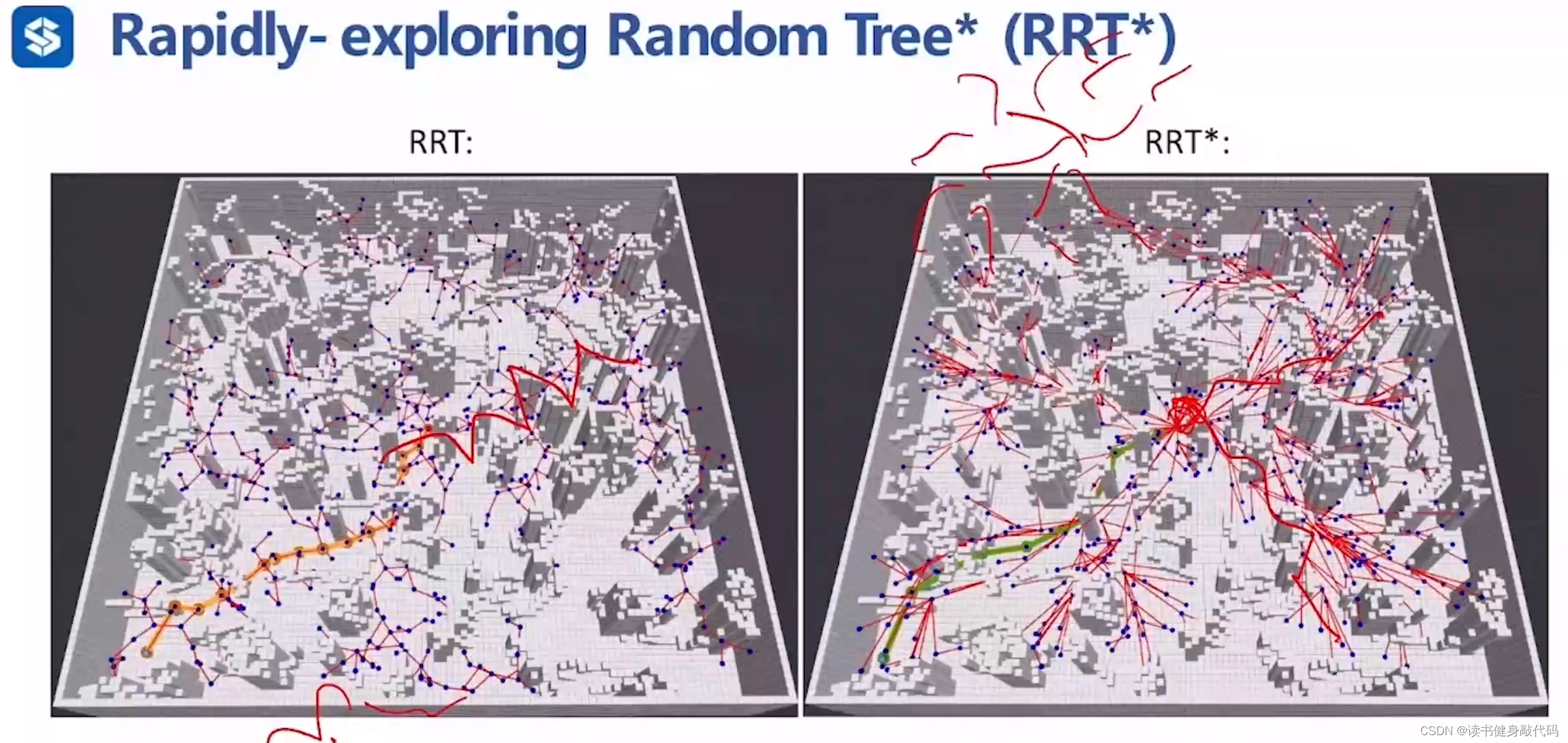
在这里插入图片描述
ZJU repo的对比。
(在找到一个可行解之后，在地图的各个方向上仍然需要不停地采样，就是因为在别的方向上可能存在f值更小的解。)

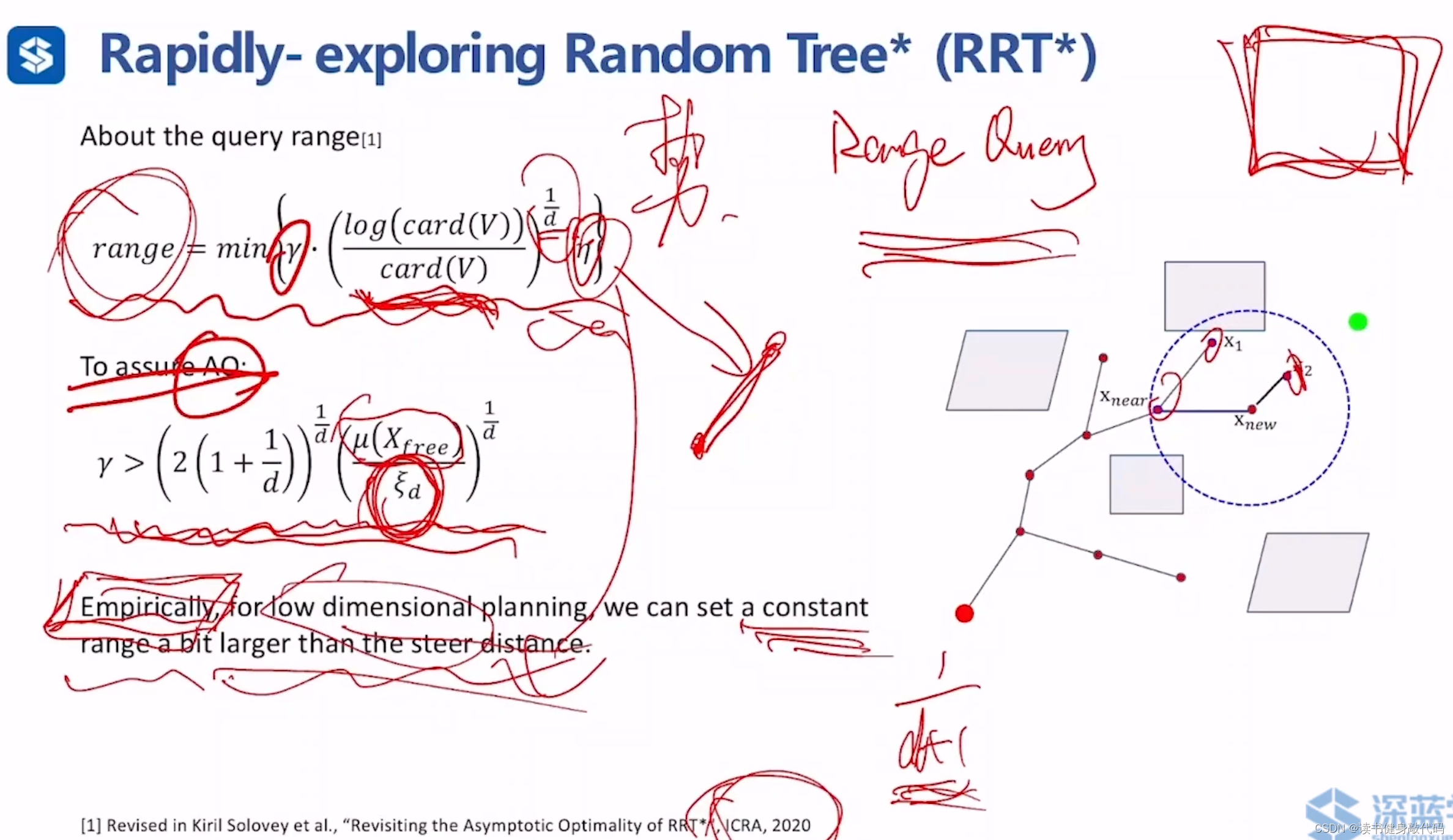
在这里插入图片描述

关于上述query range的取值：
$range=min\{\gamma * (\frac{log(card(V))}{card(V)})^{\frac{1}{d}},\eta\}$
其中

$\eta$ ：在 $x_{near}\to x_{new}$ 方向上 $s t eer ()$ 的距离，
$c a r d (V)$ ：集合 $V$ 的势，即集合 $V$ 元素的个数。
$d$ ：规划的维度
$\gamma$ ：为了保证渐进最优性(Asymptotic Optimality，AO)， $\gamma$ 必须大于某个值，即
$\gamma>[2(1+\frac{1}{d})]^{\frac{1}{d}}*[\frac{\mu(X_{free})}{\xi_d}]^{\frac{1}{d}}$
其中
- $\xi_d$ ： $d$ 维单位球的体积(volume)

定性分析，query range设置的越大，找到全局最优的可能性越大，然而，在工程上，通常没有时间让算法收敛到全局最优，我们可以设置一个比steer(即 $\eta$ )大一点点的常数去跑，也能达到比较好的效果，尤其对低维的路径规划问题。
原始RRT* paper中提出了上述计算query range的公式，在2020年的这篇文章 $^{[2]}$ 中对query range进行了改进，将 $\frac{1}{d}$ 改为 $\frac{1}{d+1}$

2.3 pratical implementation

介绍一些工程实现trick
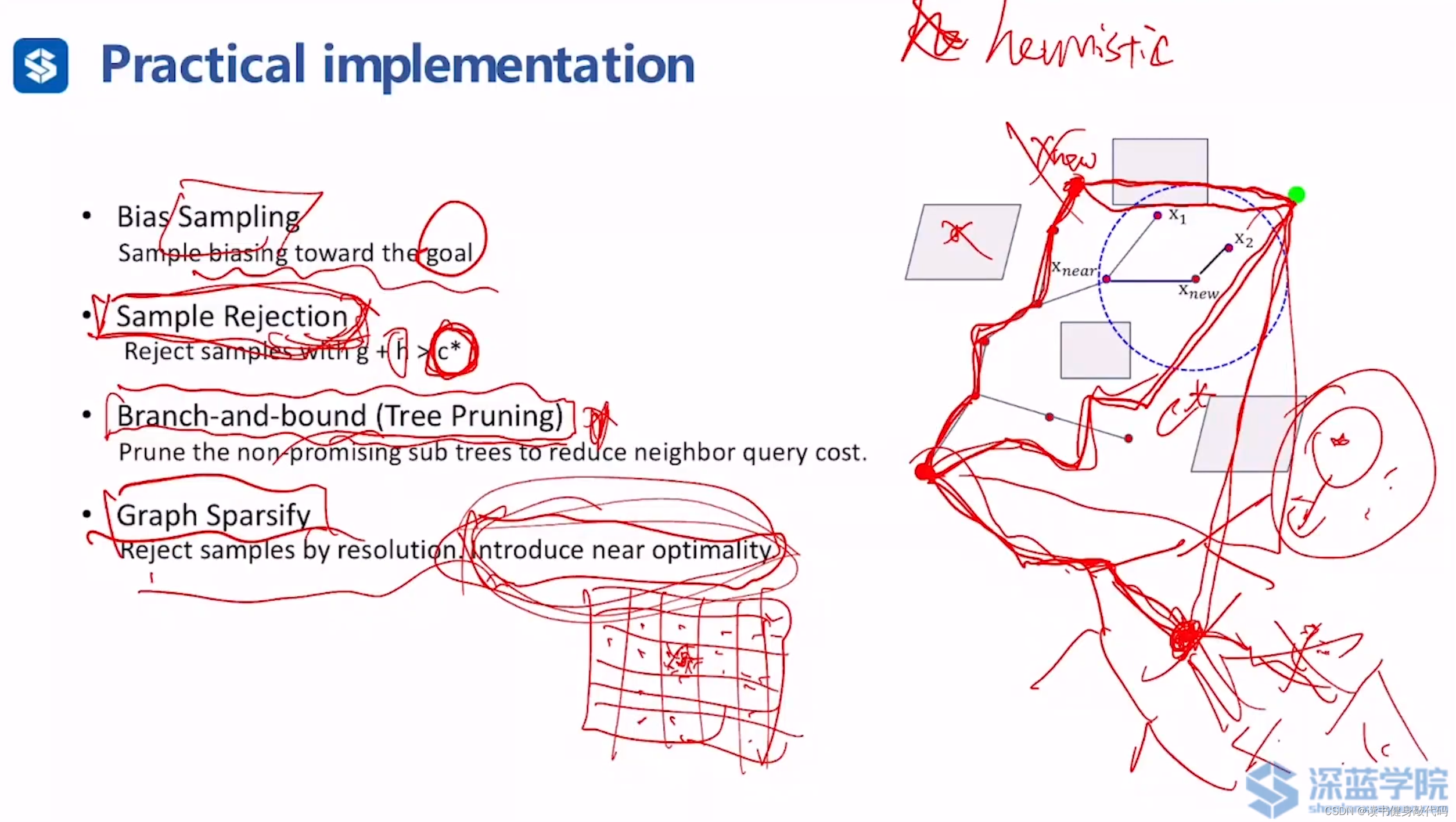
在这里插入图片描述

2.3.1. Bias Sampling

关于采样策略的改进，朝着目标点采样，比如设置一些阈值，当大于阈值时，直接使用goal当做 $x_{rand}$ 。类似的采样策略有很多，后面再细讲。

2.3.2. Sampling rejection

在某些情况下拒绝某些采样，比如有了一个feasiable的解，其cost-to-come valu= $c^{*}$ ，设计一个admissiable heursitic，用于计算到goal的cost的估计，即h，这个estimation由于是admissiable的，所以会比真实的cost-to-come value小。

对于一个新采样点i，可得g，可以计算 $h_{i\to goal}$ ，当 $f=g+h>c^{*}$ 时，我们就reject这次采样。

2.3.3. Branch-and-Bound（Tree pruning树剪枝）

跟DT的剪枝有些相似，思想和Sampling rejection相似，别的 $f = g + h$ 的值很大的子树(non-promising的树)可以选择减掉，后面不再搜索，降低后续query的复杂度。但由于只是local的认为子树是non-promissing的，并不是global的，即可能在该子树后面存在到goal更小的cost的节点存在，所以这种trick也是精度和效率的一个trade-off。

2.3.4. Graph Sparsify

将搜索空间分成很多格子，在每个格子内只留一个采样点，在离散空间(在某个resolution下)是最优，但在连续空间引入了次优性。

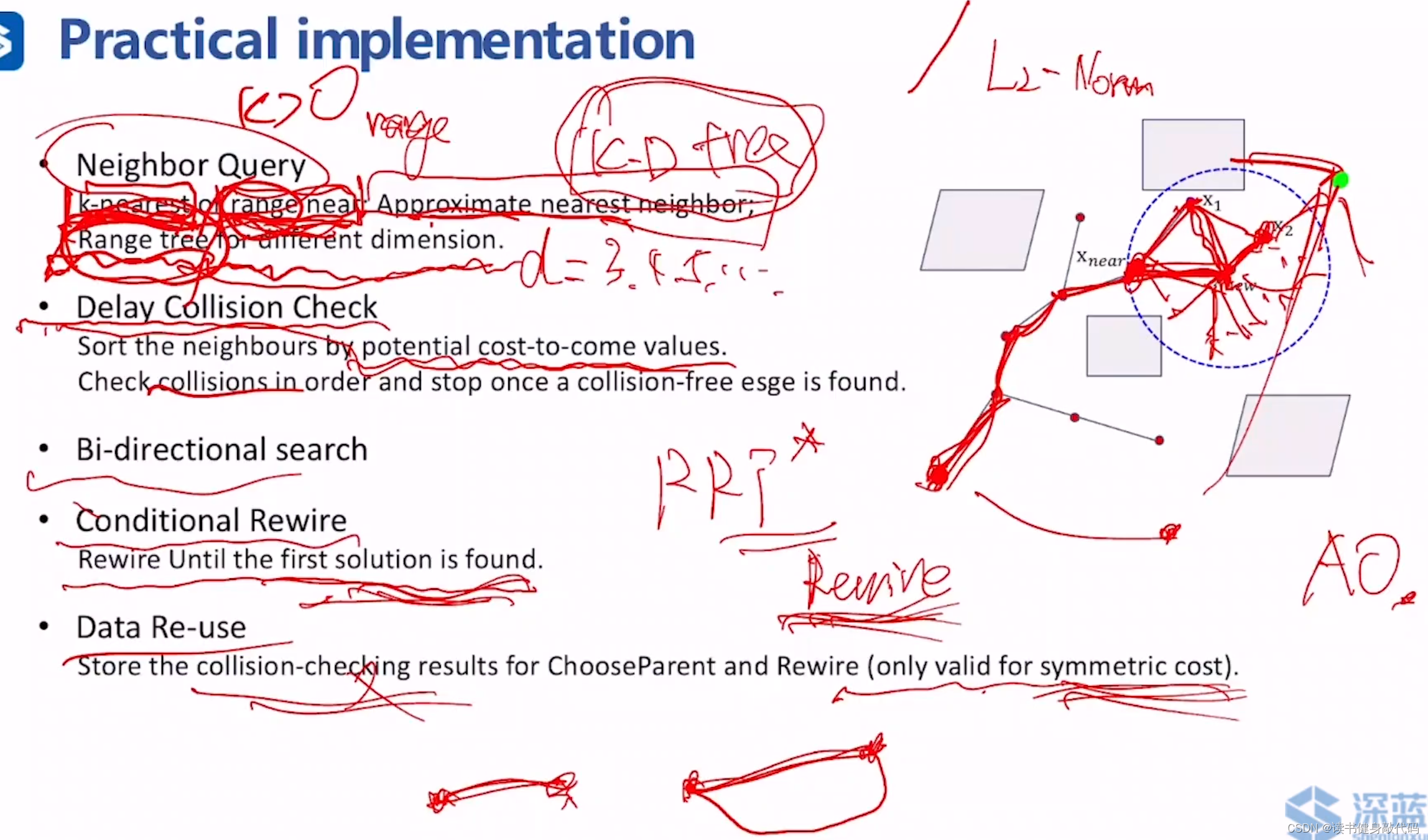
2.3.5. Neighbor Query

在 $x_{new}$ 的query range内搜索，或者是找最近的n个点(kNN)，数据结构使用K-D tree或者Range tree(针对高维情况，每一维的range计算方法不同的情况)

2.3.6. Delay Collision Check

lazy-collision-check的一种方法，在loop遍历所有parent candidates前，可以先对各个potential cost-to-come value f=g+h值进行升序排序，先从f值低的开始check，找到第一条collision-free的path的parent candidate之后，后面的就可以不再遍历了。当节点较多时提升较大。

2.3.7 Bi-directional search

从start和goal各长一棵树，在中间汇合，若要保证AO(渐进最优性)，则需要设计树的连接方式。

2.3.8 Conditional Rewire

由于rewire需要消耗计算资源，在找到第一条feasiable solution之前，仅使用RRT，不使用rewire，找到之后再开始rewire。

2.3.9 Data Re-use

保存collision-checking results for ChooseParent and Rewire，仅适用于对称的cost。
在这里插入图片描述

3. Accelerate Convergence

前面讲了找feasiable path和找渐进最优的path，我们希望算法收敛的速度越快越好，所以有对于加速收敛方面的研究。

3.1 RRT#（exploitation角度）

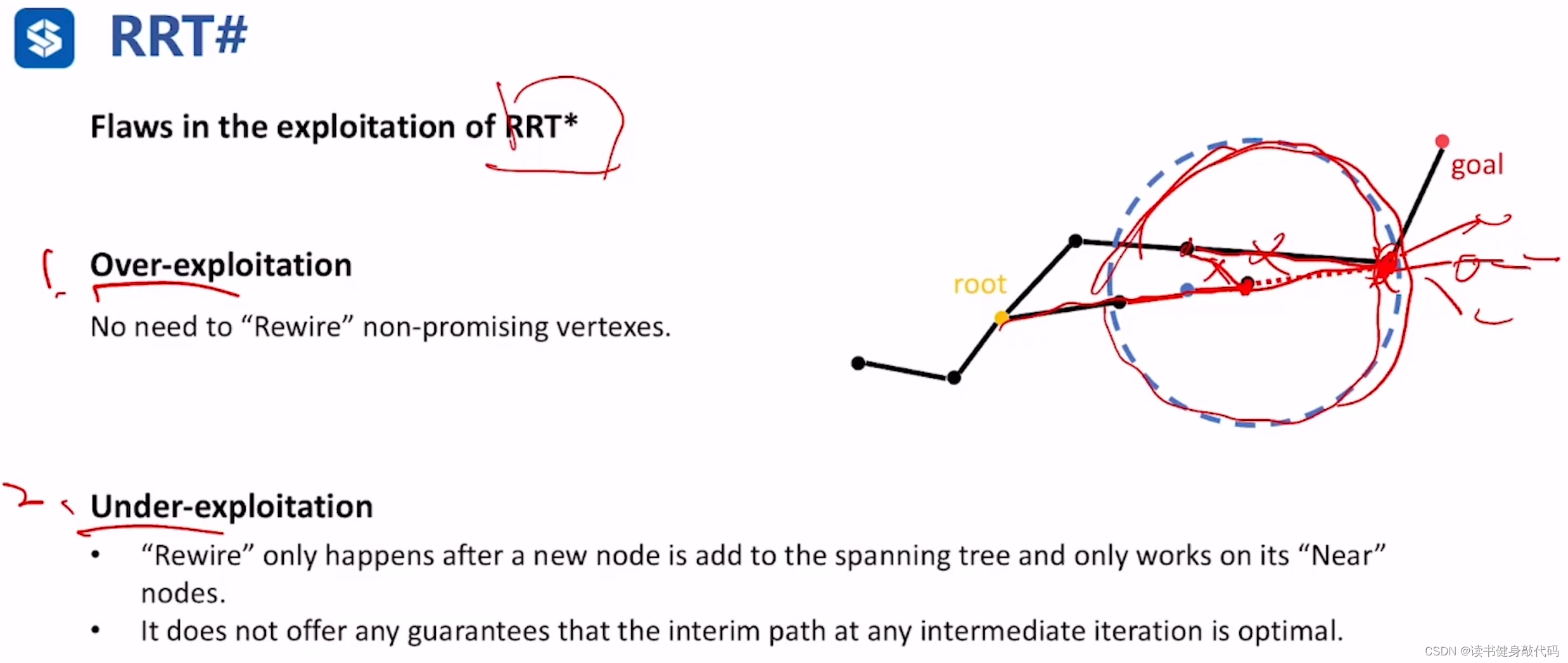
RRT#从两个方面对RRT*进行了改进：Over-exploitation，Under-Exploitation
在这里插入图片描述

Over-exploitation(过度利用，属于规划问题的exploitation phase，对已有树的优化)
和Sampling rejection有些类似，Sampling rejection是在sampling阶段选择采样点，通过计算potential sampling point的heuristic，进而得出 $f = g + h$ 与已有的 $c^{*}$ 进行比较，而Over-exploitation是在找到了parent之后，再rewire阶段再次使用heuristic(当然这两个heuristic可能不一样)，如果 $f=g+h>c^{*}$ ，则无需对该candidate进行rewire操作。
Under-Exploitation(欠利用，同属exploitation phase)
这个不太理解，感觉没讲清楚。PPT上说的是Rewire仅在新节点被加到spanning tree中之后才进行，且只对其Near节点进行(我觉得不加到tree中也没必要rewire啊？在query range中肯定只对Near进行啊？这个需要看paper才能深入理解。)

RRT#的工程实现代码可能比较复杂。
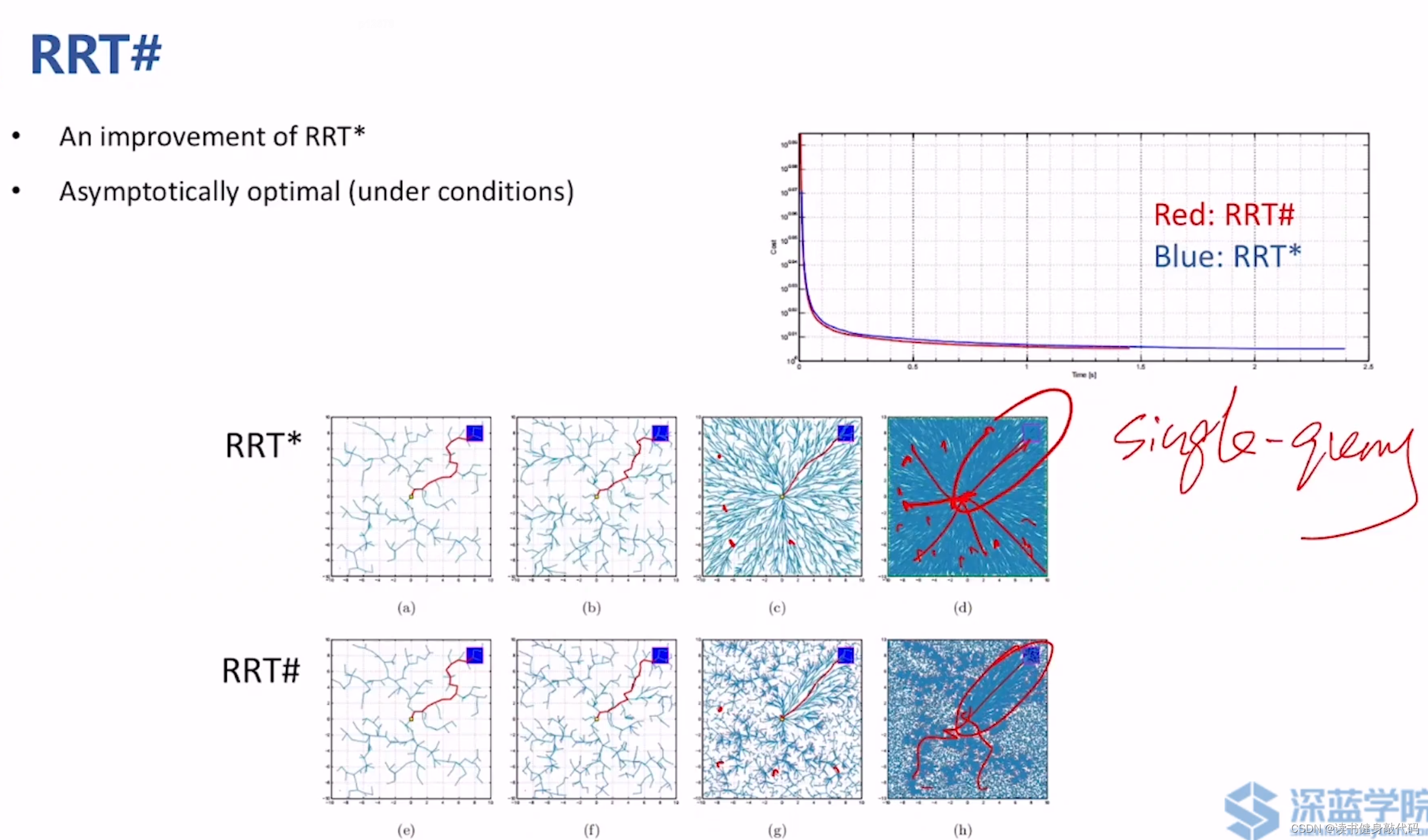
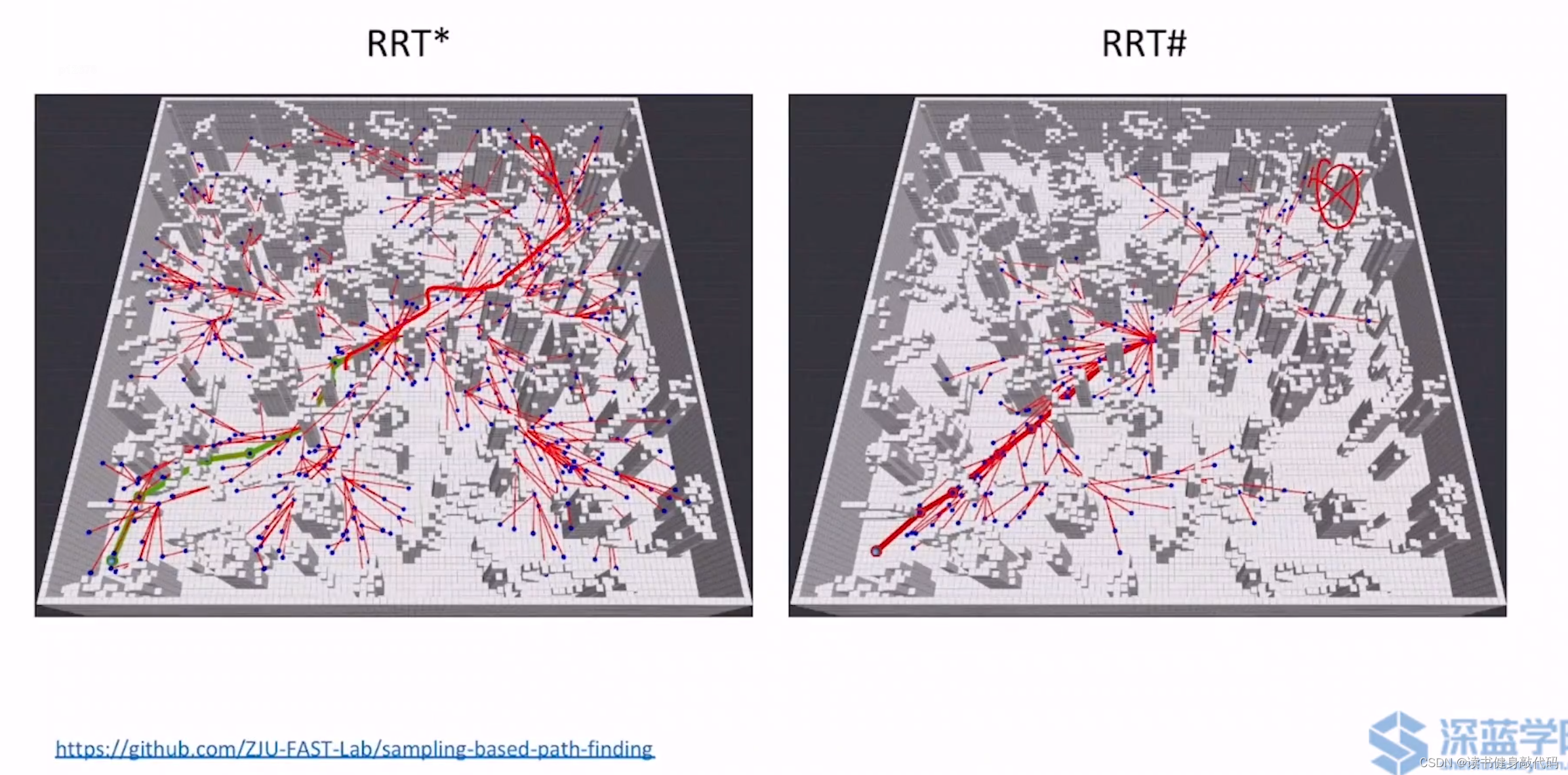
在这里插入图片描述

在这里插入图片描述

上面两图可以直观地看出，RRT#是更优目标性，找到 $c^{*}$ 之后，其他方向的扩展就很少了，基本不操作，而RRT*仍然是继续扩展，保证了多个方向的较优的solutions。RRT#更适用于single query。

3.2 Informed sampling(exploration角度，smapling strategy)

informed sampling信息采样，通常指一种采样策略，它利用已有的问题解决方案信息来引导采样过程，以提高搜索效率和寻找更优解的概率。
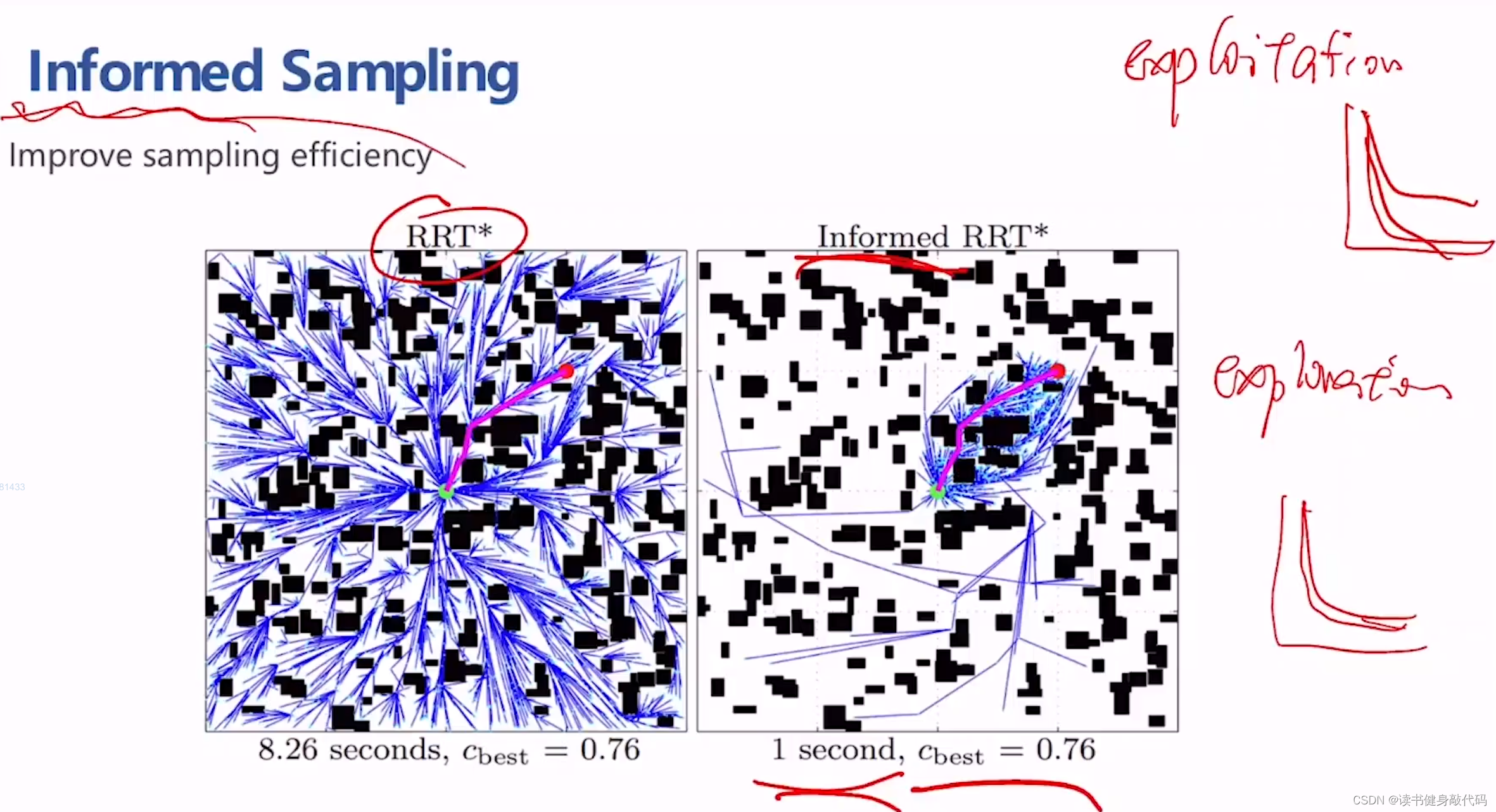
在这里插入图片描述
直观理解，比RRT*更快地找到AO解。

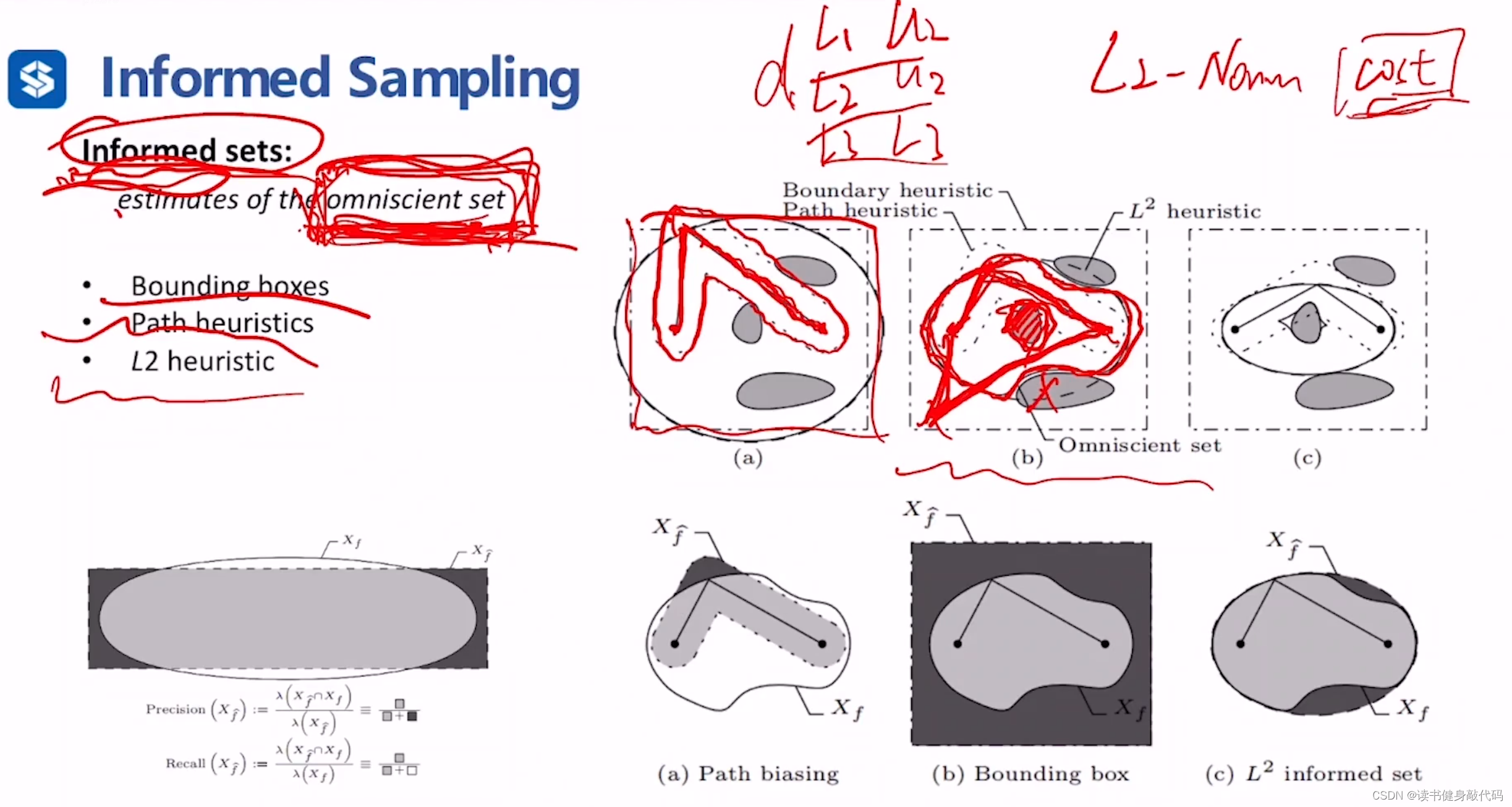
在这里插入图片描述
简单理解即缩小采样的范围，且缩小后的范围要合理。

omniscient set(全知集)是对求解有提升的采样范围，我们需要设计一个sets，作为omniscient sets的estimation，称作informed sets（信息集）

缩小后的范围为，有三种缩小方式：

Bounding box：在每一个维度上找到一组(lower bound, upper bound)用于缩小sampling范围
Path heuristics：只在已有的feasiable path附近搜索
L2 heuristic：以start和goal为椭圆两焦点，以当前已有的最优解为长轴之长(椭圆是平面上到两个相异固定点的距离之和为常数的点之轨迹) 绘制椭圆，以此椭圆为informed sets。

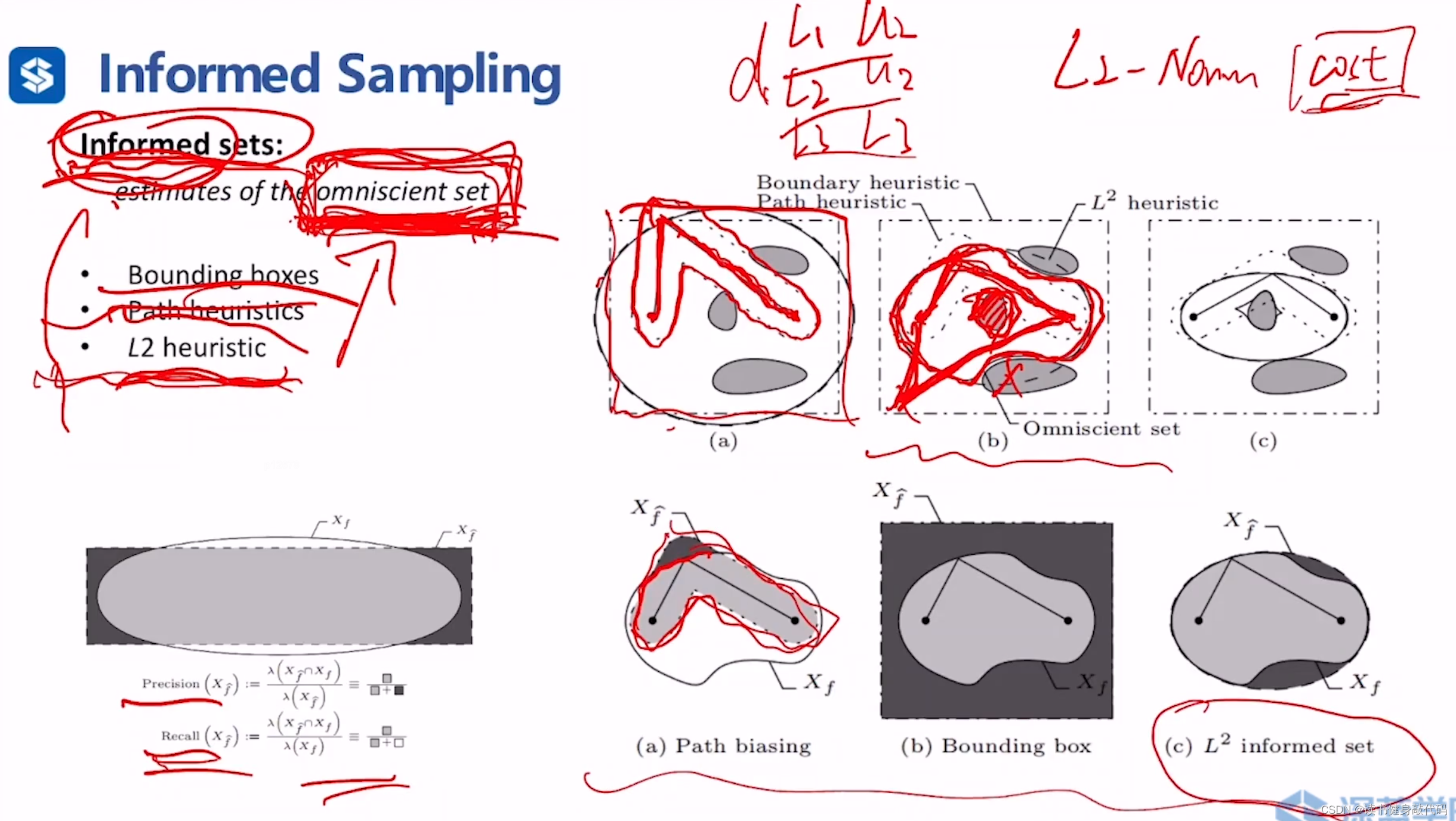
在这里插入图片描述
两个metrics：

precision：准确率，informed sets中属于omniscient set点在informed sets中的比例。
recall：召回率，informed sets中属于omniscient set点在omniscient set中的比例。

以上三种informed sets，L2 heuristic的precision和recall均为最高。

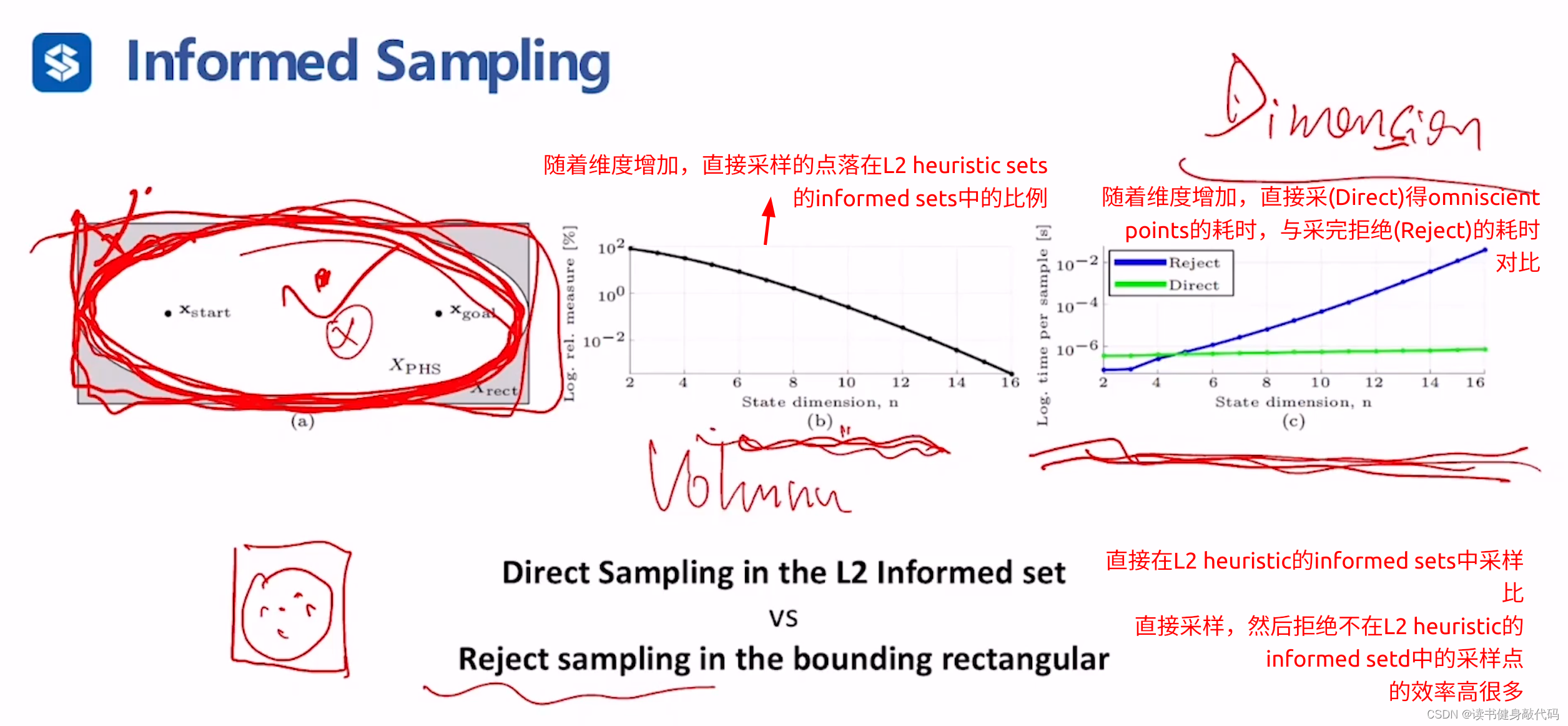
在这里插入图片描述
针对L2 heuristic informed sets有两种策略：

直接在informed sets内采（Direct）；
直接全部采，然后拒绝不在informed sets中的（Reject）。

Direct策略更优，随着维度增加，Reject采到omniscient sets中的点比例下降，且耗时增加。

在这里插入图片描述
探究为什么L2 heuristic informed set有效：

对于使用L2 heuristic informed sets，需要使用L2 norm作为cost的计算方法。

admissiable heuristic $\leq$ 最优解，是对最优解的下界的估计，如果 $c^{*} \leq$ 采样点的admissiable heuristic，则必有： $c^{*} \leq$ 采样点的admissiable heuristic $\leq$ 经过此采样点的最优cost

实际实现方法：

unit ball：在单位圆(或者高维的单位球)内进行采样；
scale：将圆进行放缩为椭圆；
Rotation：将椭圆进行旋转；
Translation：将椭圆进行平移。

L2 informed set的局限性：只能用于cost function为L2 norm时，如果不是，则无法显式设计出informed set。

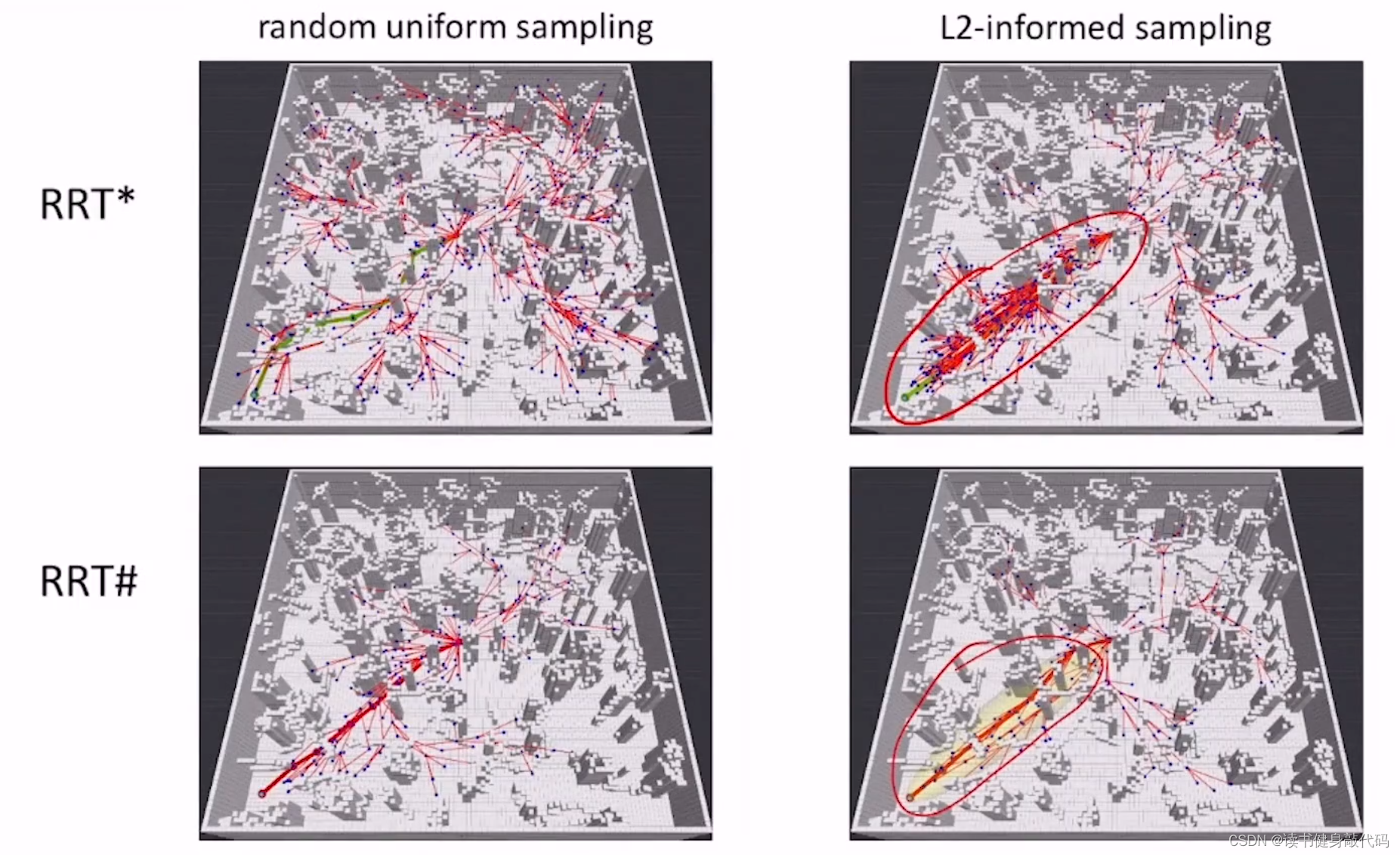
在这里插入图片描述
L2-informed set在RRT*和RRT#上的使用。

3.3 GuILD(exploration角度，smapling strategy)

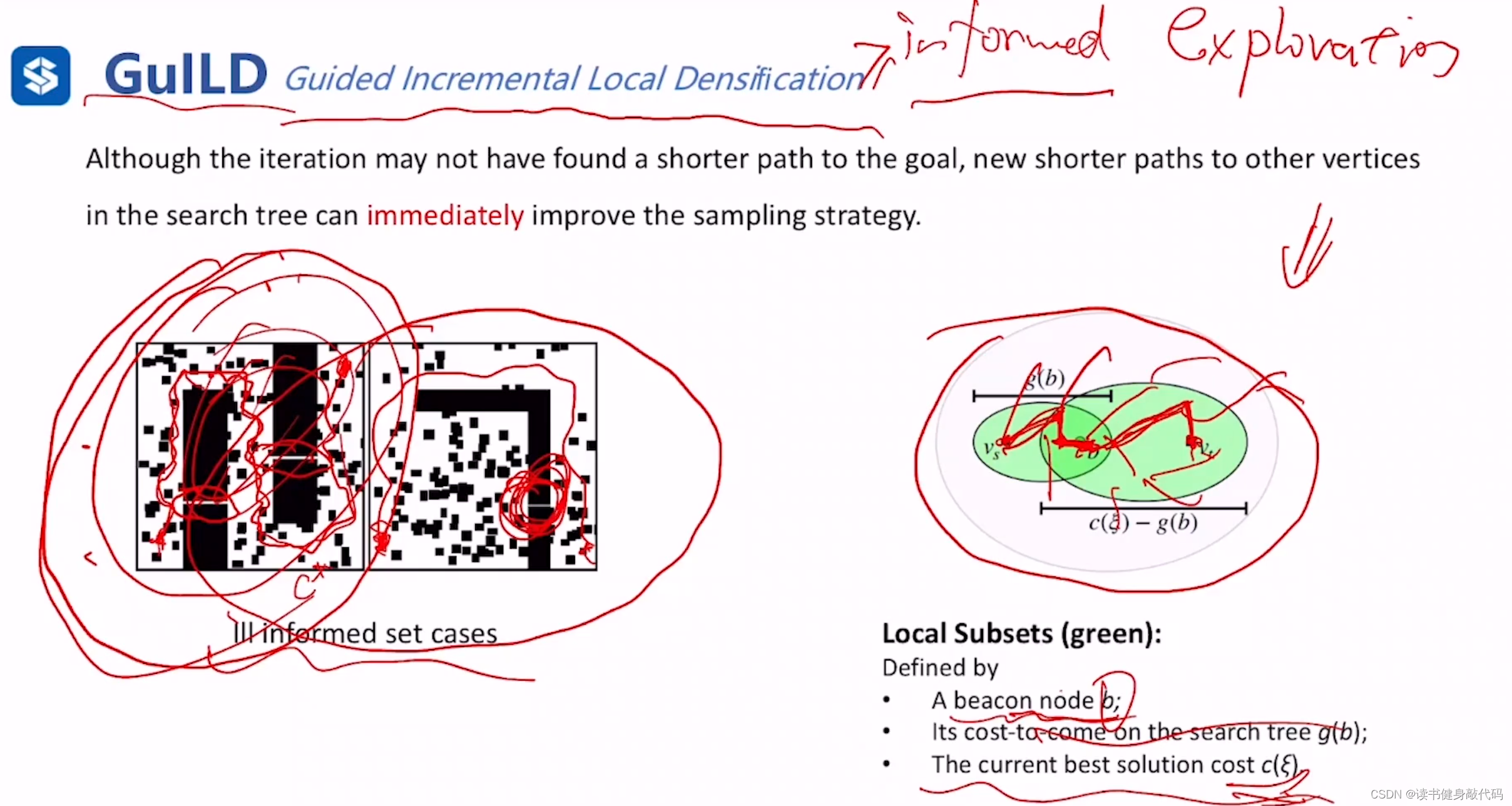
在这里插入图片描述

informed set缩小的条件是当前最优cost变小，此方法对于窄缝中的点很难采样到，如果最优路径需要经过这些窄缝中的点，那么informed set很可能很难缩小搜索范围。

GuILD提出了将informed set分为两部分：

在当前的树中找一个beacon node(信标点)b，
计算出g(b)，以start和b作为焦点，g(b)作为长轴之长绘制椭圆 $t_1$
当前最优解的cost为 $c(\xi)$ ，以b和goal为焦点，以 $c(\xi)-g(b)$ 为长轴之长绘制椭圆 $t_2$

则之前单独的informed set(IS)被分解为 $t_1,t_2$ 两个local subsets(LSs)，总体cost仍然为 $c(\xi)$ ，已经证明：LSs的估计是IS的upper bound(上界)

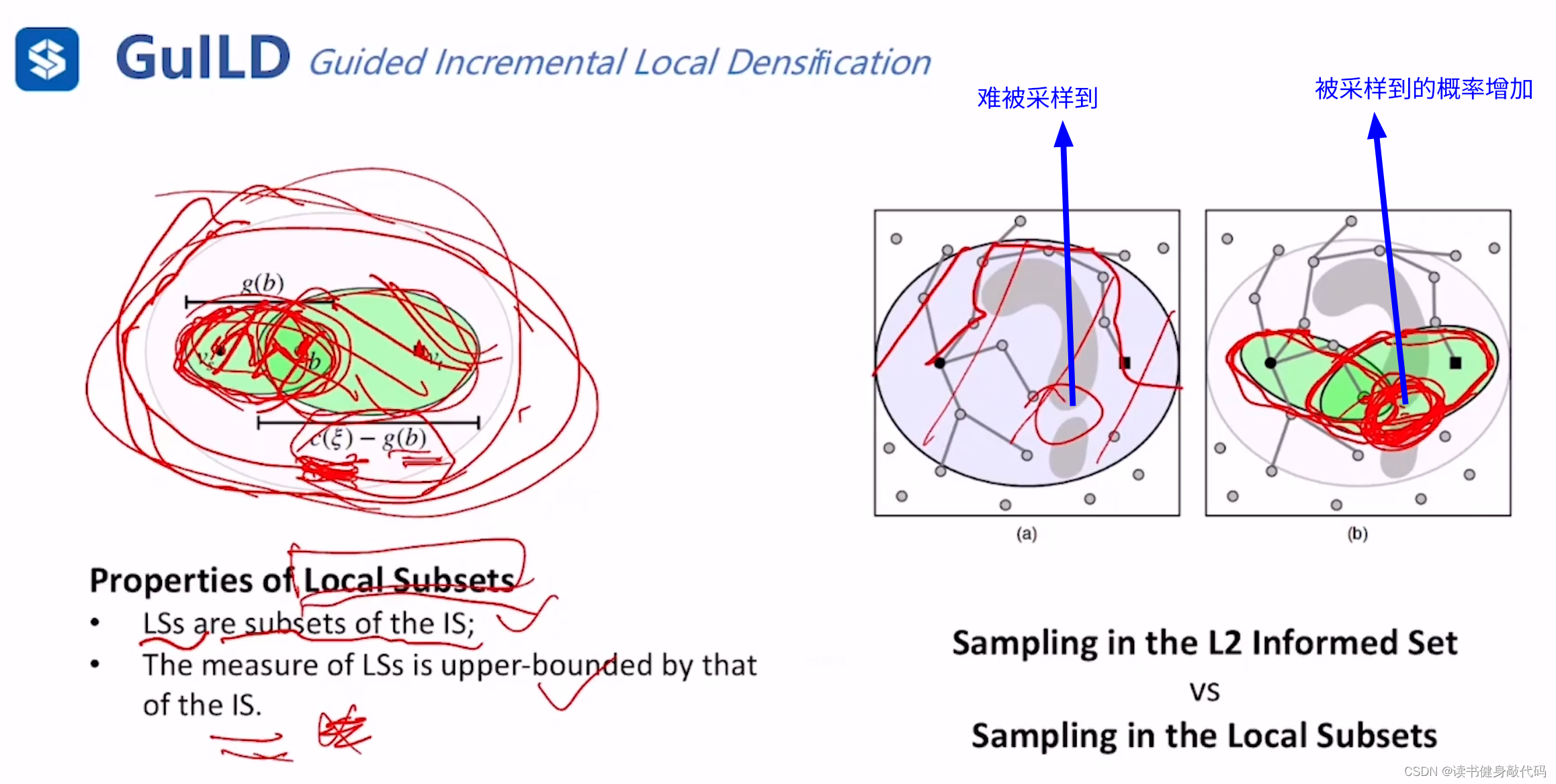
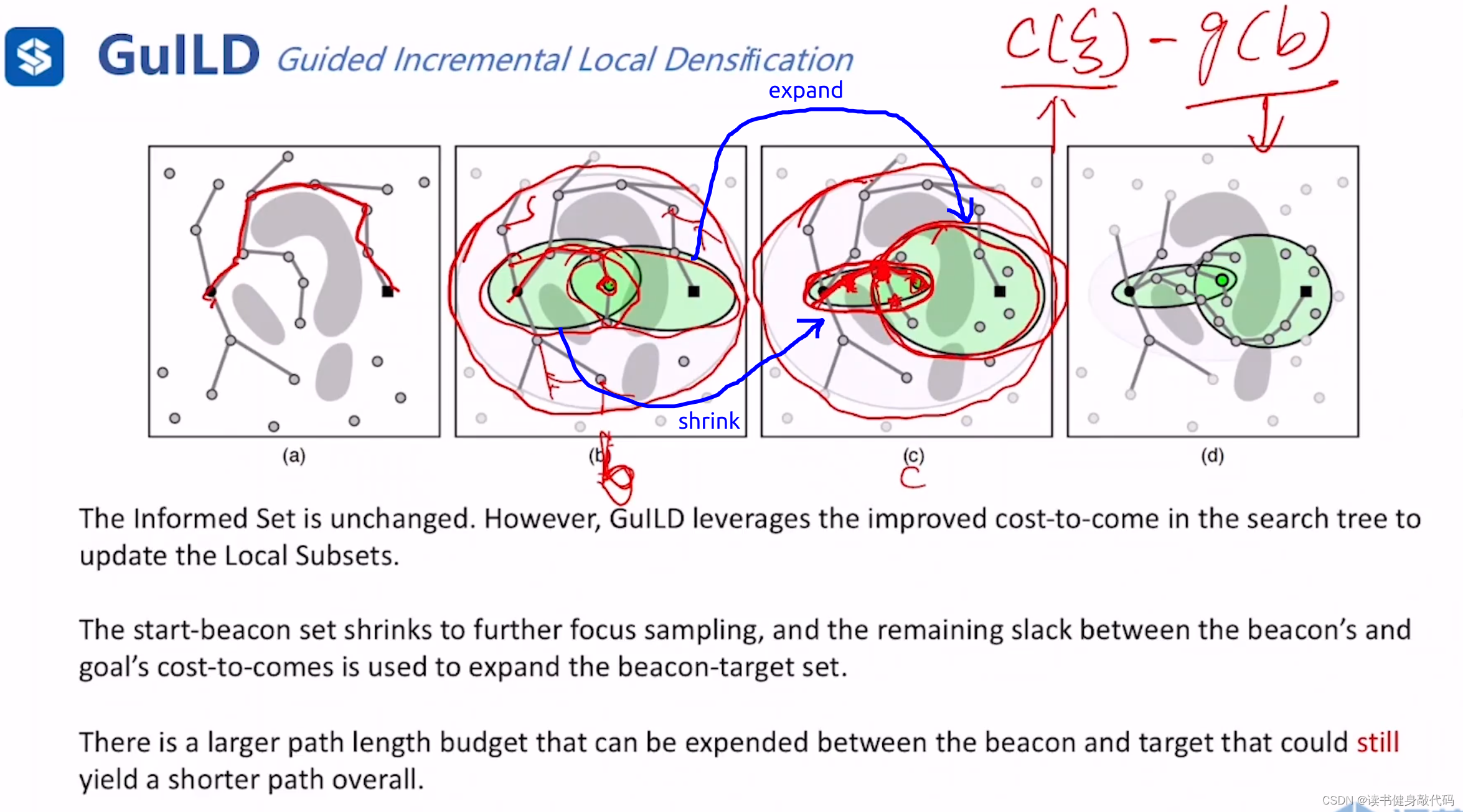
在这里插入图片描述

一个关键的变化是在整体 $c(\xi)$ 没有变化时，start-beacon set会由于搜索过程中找到了更小的cost的path而被shrink，所以beacon-goal set会被expand，增大了找到窄缝中点的概率。

4. Development trend

本章从三个方面简单讲述了sampling-based path methods以及一项最近的研究：

Feasiable（PRM，RRT）；
Optimal（RRT*，implenmentation trick）；
Convergence（RRT#，Informed RRT*，GuILD(2022)）

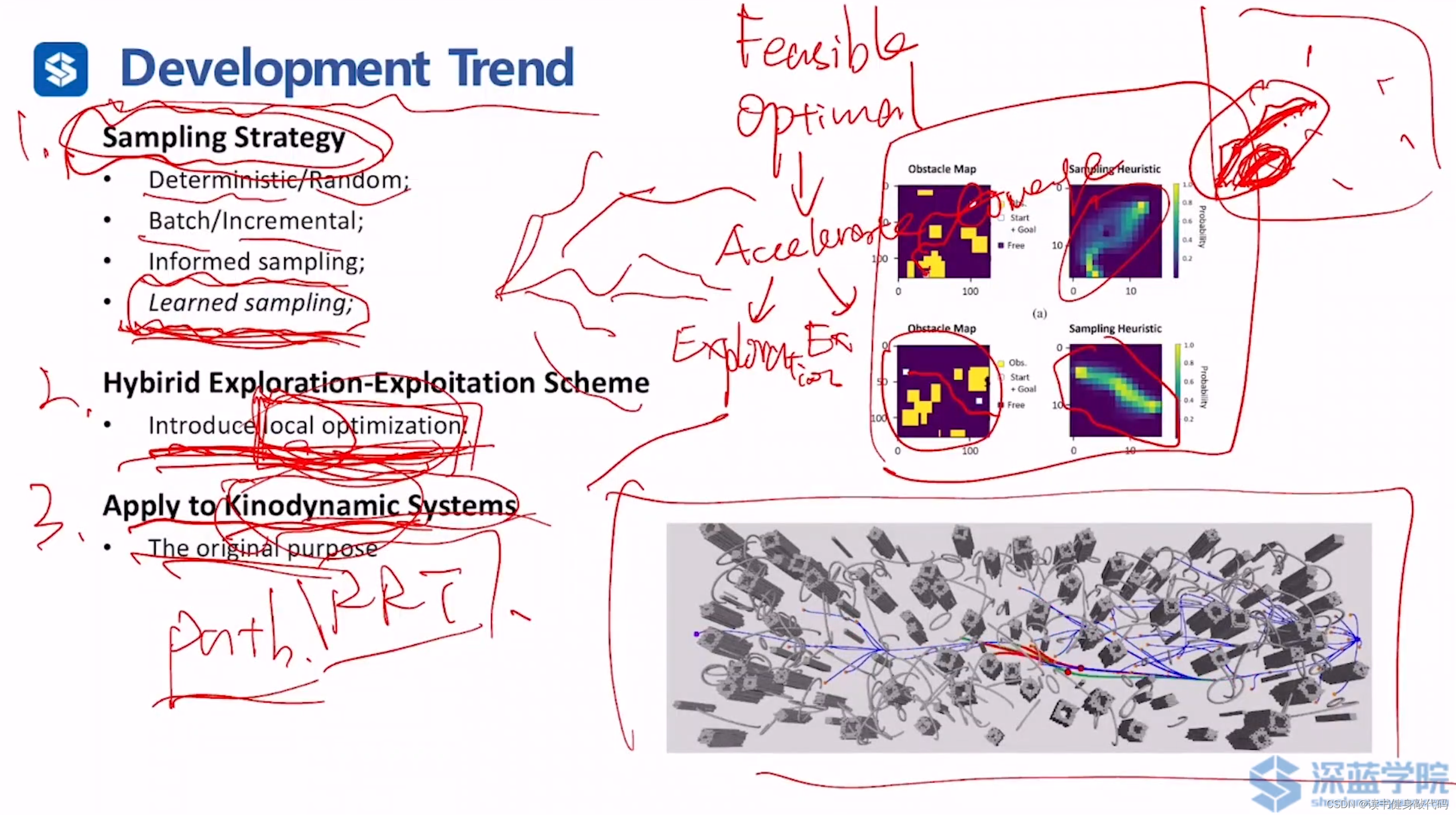
在这里插入图片描述
sampling based methods关于Exploration方面的发展比较有潜力：
4. Sampling Strategy：
1. Deterministic/Random：确定的/随机的
2. Batch/Incremental：批量的/增量的
3. Informed sampling
4. Learned sampling（右上图的右侧代表了DL学习出的类似于informed sets的采样范围，当然这类方法还在发展当中，目前可能只能适用于一些简单情况）

混合的方法(Exploration和Exploitation混合的方法)：如引入局部优化（上右下图引入了局部优化，原来绿色边变为红色边，更顺滑）
应用于带有动力学约束的系统：原本RRT提出的初衷就是为了应用于实际的动力学系统。最开始是应用于系统规划，慢慢应用到path planning中。

一些库，框架
在这里插入图片描述

OMPL功能非常强大的一个Motion Planning库，功能强大且完整，在ROS中也有集成。
Moveit with ROS，使用于机械臂(Manipulation)的MP的库
Fast-lab(ZJU FAST-lab的库)

5. Assignment

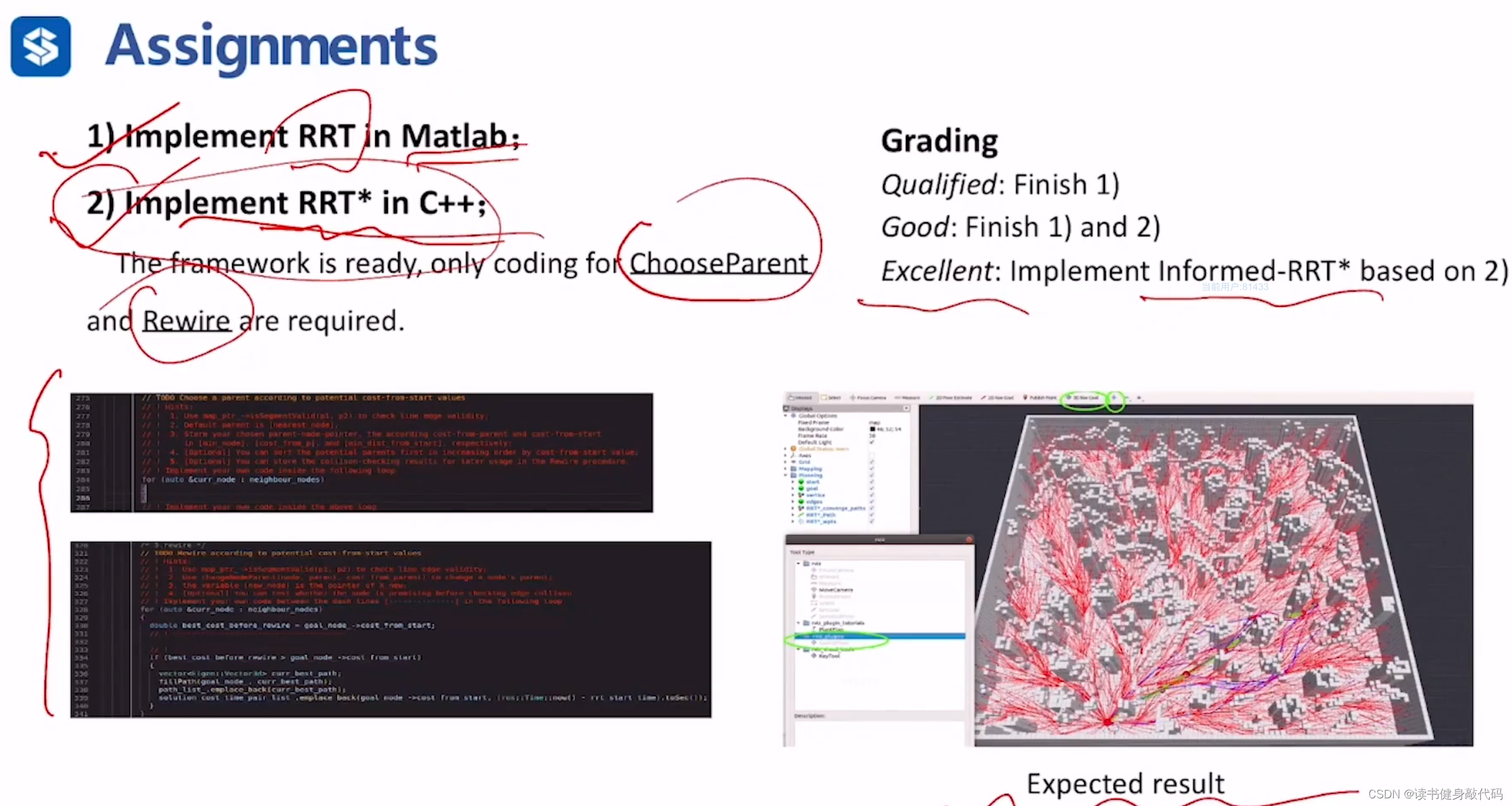
在这里插入图片描述

6. Reference

[1] Karaman, S., & Frazzoli, E. (2010). Incremental Sampling-based Algorithms for Optimal Motion Planning. ArXiv, abs/1005.0416.
[2] Solovey, K., Janson, L., Schmerling, E., Frazzoli, E., & Pavone, M. (2019). Revisiting the Asymptotic Optimality of RRT*. 2020 IEEE International Conference on Robotics and Automation (ICRA), 2189-2195.
课程中提到的参考论文：

在这里插入图片描述

这篇关于【深蓝学院】移动机器人运动规划--第3章基于采样的路径规划--笔记的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

【深蓝学院】移动机器人运动规划--第3章基于采样的路径规划--笔记

0. Preliminaries