本文主要是介绍Coursera 机器学习(by Andrew Ng)课程学习笔记 Week 1——简单的线性回归模型和梯度下降,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
此系列为 Coursera 网站机器学习课程个人学习笔记(仅供参考)
课程网址:https://www.coursera.org/learn/machine-learning
参考资料:http://blog.csdn.net/scut_arucee/article/details/49453033
1 Introduction
1.1 机器学习的定义
Arthur Samuel 将其描述为:the field of study that gives computers the ability to learn without being explicitly programme.
另一种更为现代化的定义是:A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.
所有的机器学习问题都可以划分为两大类:监督学习(Supervised learning)和无监督学习(Unsupervised learning)。
其他分类还有增强学习(Reinforcement learning)、推荐系统(Recommender system)。
1.2 监督学习(Supervised Learning)
监督学习与无监督学习的区别就是:“right answers” given,即用于训练的数据已经提供了一组“标准答案”。
监督学习问题又可以分为 1.回归问题(Regression)和 2.分类问题(Classification)。
回归问题:predict continuous valued output,即需要预测的变量是连续的。
例如:已知一组数据,包含房屋的面积(x)和对应的价格(y),预测当房屋面积为特定值时(x=x0)对应的价格为多少。
分类问题:discrete valued output,即需要预测的变量的离散的(0 or 1)。
例如:已知一组数据,包含肿瘤的大小(size)和对应的性质(良性/恶性)(0/1),当给出肿瘤的大小时,判断其为良性还是恶性。
1.3 无监督学习(Unsupervised Learning)
无监督学习与监督学习的区别是:no right answer,即没有给定标准答案,预测的答案不会给出任何反馈,根据数据的结构和关系将它们进行聚类。
clustering:网页将每天发生的各类新闻分类,相似的新闻会归到一类。
non-clustering: The “Cocktail Party Algorithm”,将人说话的声音与背景音乐分离。
2 Model Representation
首先我们定义几个符号:
2.1 假设函数(hypothesis)
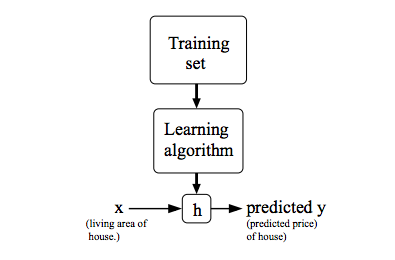
对于监督学习,我们的目标是,给定一个数据集,通过学习算法得到一个函数 h:X→Y ,使得可以从 h(x) 中很好的预测出与 x 相对应的
以房价预测为例,房屋面积为
2.2 代价函数(cost function)
有了 hθ(x) (hypothesis function)我们如何得到 θ0 、 θ1 的值呢?我们的优化目标是选择 θ0 、 θ1 使得 hθ(x) 在训练数据集上尽可能地靠近 y 。我们可以使用均方差来衡量
为了后面求导的方便,我们在前面乘了一个 12 ,并不会影响后面的结果。
这时,我们可以定义我们的代价函数(cost function):
这个函数也称为均方差函数(squared error function),是回归问题中最常见的代价函数。后续还会讲到其他类型的代价函数(cost function)。
3 代价函数(Cost Function)
代价函数(cost function)也称为损失函数(loss function)
下面我们会举几个例子来看一看代价函数是怎么工作的以及它的作用。
为了简化,我们设 θ0=0 ,此时, hθ(x)=θ1x , J(θ1)=12m∑mi=1(θ1x(i)−y(i))2 。
首先我们区分一下 hθ(x) 和 J(θ1) :
hθ(x) : θ1 固定,是关于 x 的函数;
J(θ1) :是关于 θ1 的函数;
例如,给定的三组训练数据,我们可以在 (x,y) 坐标系中做出不同 θ1 对应的 hθ(x) 的图像,如下 hθ(x) 分别取 1 ,
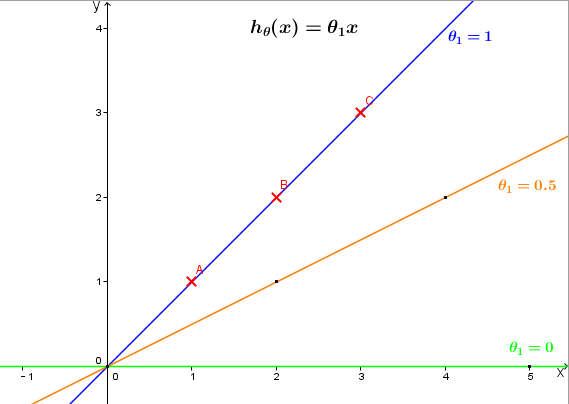
分别计算代价函数
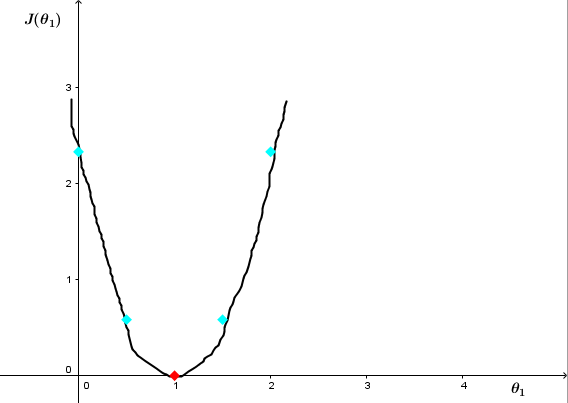
可以看出当 θ1=1 时, J(θ1) 最小。 J(θ1) 图像中,不同的 θ1 对应 hθ(x) 图像中不同的(过原点的)直线。
接下来我们通过轮廓图(contour plots)更加深入地了解代价函数(cost function)的作用。上面 J(θ) 函数只有一个参数 θ1 ,可以看出 J(θ) 的图像像一个弓形,而当 J(θ) 含有两个参数 θ1 , θ0 ,那么 J(θ0,θ1) 的图像呈三维曲面,如下图所示:
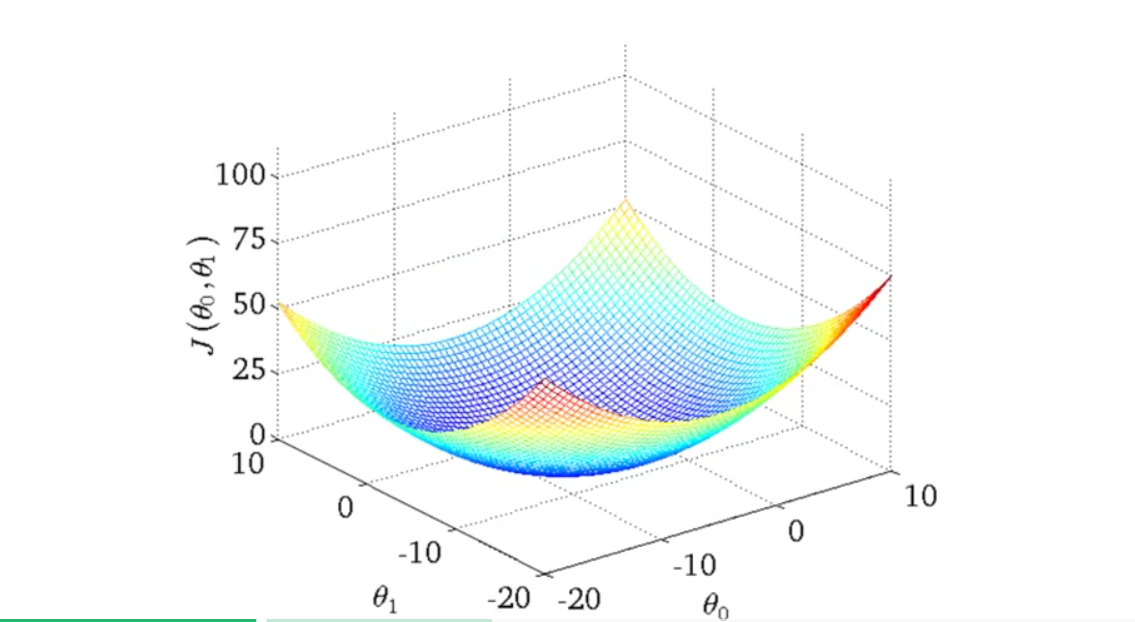
下面为了方便讲解,我们不使用这样的三维曲面,而是用轮廓图(contour plots)来代替。如下图所示:
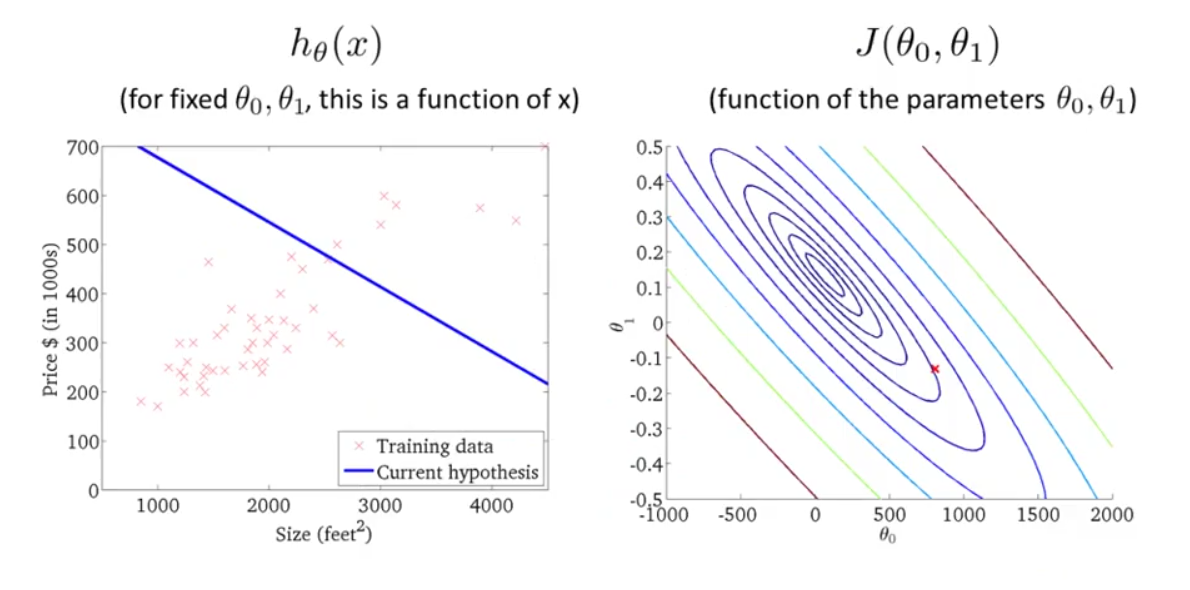
右图 J(θ0,θ1) 的轮廓图,每一个圆圈代表 J(θ0,θ1) 值相同的所有点的集合。最小值是中心点。
图中红色的交叉点代表某个 (θ0,θ1) 数值组的集合, θ0=800 , θ1=−0.15 ,同时,也对应与左边的一条直线。可以看出,它并不能很好地拟合左图的训练数据。而越接近中心的点 (θ0,θ1) 越能很好地拟合训练数据。
这里只有两个参数,而通常我们会遇到更多参数,更加复杂的代价函数,并不能将其可视化,但是我们要做的工作都是一样的,即找出使代价函数最小的参数值 θ0、θ1 。
4 梯度下降(Gradient Descent)
现在,我们有了假设函数(hypothesis)以及衡量其是否拟合数据的方法——代价函数(cost function),现在我们需要做的就是估计出假设函数(hypothesis)中的参数,即找出使代价函数最小化的参数 (θ0,θ1) ,梯度下降(gradient descent)是一种常用的方法。
除了最小化单变量线性回归的代价函数,梯度下降还可用于最小化更一般的代价函数:
4.1 梯度下降算法(gradient descent algorithm)
为了简化过程,我们以单变量线性回归为例(设参数只有) θ0,θ1 ,梯度下降的大致过称为:
①给 θ0,θ1 赋初始值,可以都是0
②不断更新 θ0,θ1 让 J(θ0,θ1) 减小到期望的最小值。
假设 J(θ0,θ1) 如下图三维平面,我们想象自己站在小山坡上的某点,要尽快下山,问题就变为每一步应该朝哪个方向走,才能尽快到达山底。
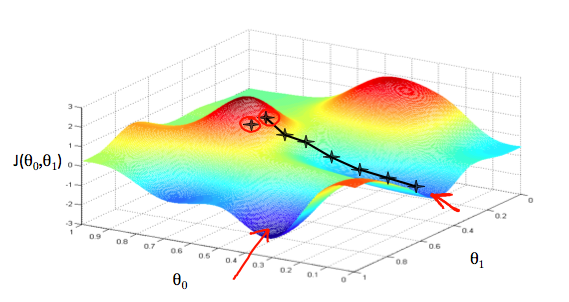
一般情况下,我们会从出发点开始环顾四周,找到最快的方向,每走一步,就环顾四周判断一次,再走下一步,直到达到局部最小值。而这种方法的特点是从不同的出发点出发,我们最终到达的可能是不同的局部最优解,如图。关于这个问题,我们之后再进行讨论。
用更加数学化的方式总结梯度下降的算法,即,重复直到收敛:
A:=B 表示把B赋值给A, α 称为学习率(learning rate),可以理解为我们每一次更新的步长,决定了每次更新的幅度。后面我们会讲如何设置 α 。
4.2 同时更新(simultaneously update)
在上面给出的更新式子中,我们需要每次更新的参数是 θ0,θ1 ,但需要注意的是两个参数需要同时更新(simultaneously update)。看下图,左图为正确的更新步骤,右图为错误的更新步骤。

简而言之,就是不能将此次已经更新过的 θ0 的值用于此次 θ1 的更新。
4.3 梯度下降如何实现最小化代价函数
那么为什么梯度下降可以用于最小化代价函数呢?即,梯度下降如何实现一步步更新后, J(θ) 越来越靠近最小值(山底)?
为了方便说明,我们仍假设 θ0=0 ,则:
其中, ddθ1J(θ1) 即为点 (θ1,J(θ1)) 出的切线斜率。考虑以下三种情况:
1、若 θ1 在局部最优解的右边:
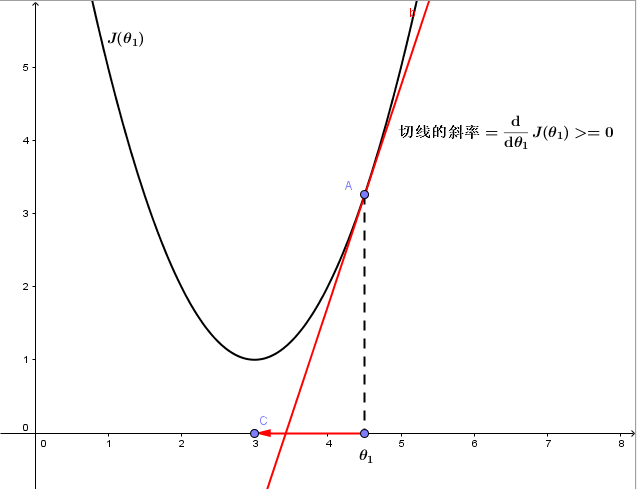
ddθ1J(θ1 永远大于等于0,且 α 永远为正,所以 θ1 将减小,向坐标轴左侧移动,即向代价函数 J(θ1) 更小的方向更新。
2、若 θ1 在局部最优解的左边:
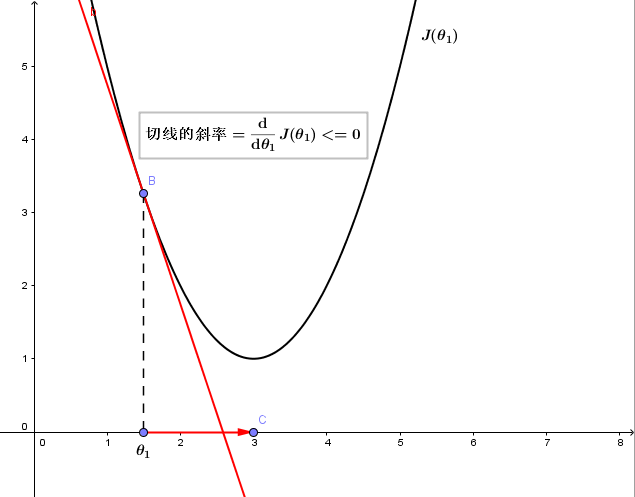
ddθ1J(θ1 永远小于等于0,且 α 永远为正,所以 θ1 将增大,向坐标轴右侧移动,即向代价函数 J(θ1) 更小的方向更新。
3、若 θ1 已经处于局部最优位置:
由于该点切线的斜率 =ddθ1J(θ1)=0 ,故 θ1 将保持不变,此时即使还存在其他 θ1 的值使代价函数更小,也只能收敛于该局部最小值,而无法收敛于全局最小值。
4.4 学习率(learning rate)
我们再来看学习率 α :
1、 如果 α 太小,则因为每次更新 θ1 的幅度太小导致梯度下降收敛很慢,如下图:
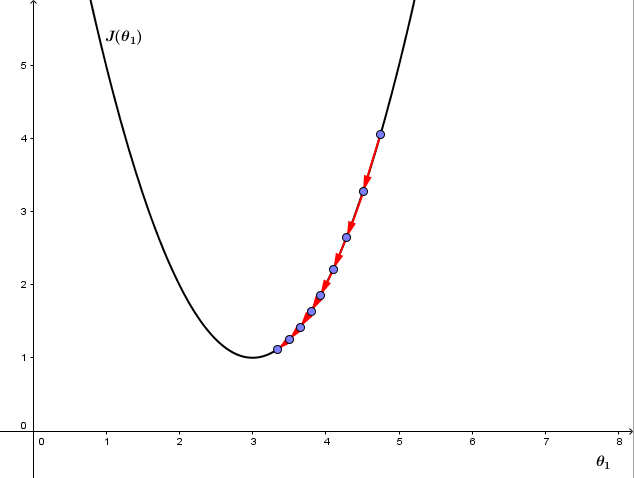
2、如果 α 太大,则梯度下降可能会跨过最小值不能收敛,甚至离收敛点越来越远,如下图:
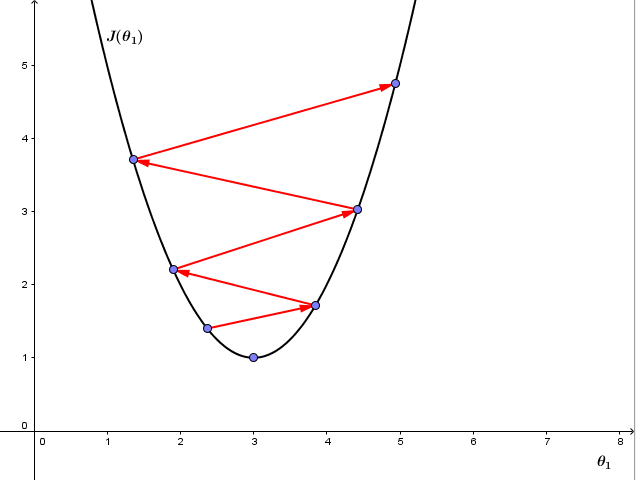
有趣的是,我们并不需要改变 α 的值,即使 α 值固定,梯度下降也能收敛到一个局部最小值。原因是代价函数在接近局部最小值的过程中,切线的斜率越来越小,即 ddθ1J(θ1 越来越小,即使 α 固定,梯度下降的步距也会越来越小,最终也能收敛到局部最小值。
4.5 梯度下降与线性回归
前面我们说过,线性回归常用的代价函数就是方差代价函数。现在,我们就将梯度下降用于最小化方差代价函数,
梯度下降算法的表达式:
根据上面两的公式,我们把等式转化为:(下图中 xi 表示 x(i) , yi 表示 y(i) )
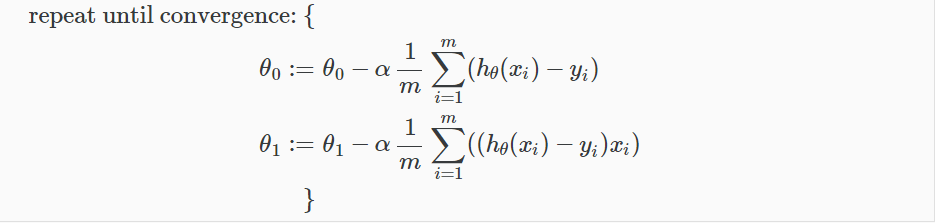
同理这里 θ0 , θ1 也是同时更新,其中 hθ(xi)=(θ0+θ1x) 是造成对 θ1 求偏导多出了 x(i) 这一项的原因。
下面我们看只一个训练数据求偏导:
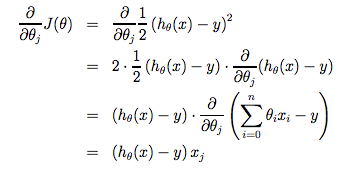
如果我们从初始值开始不断重复梯度下降的过程,我们的假设函数(hypothesis)会变得越来越准确。
4.6 批量梯度下降(batch gradient descent)
上述方法在每一步都会用到所有的训练数据( ∑ ),所以被称为批量梯度下降(batch gradient descent)。在我们用的这个特殊例子(单变量线性回归)中, J(θ0,θ1) 除了全局最优解(global optima)没有局部最优解(local optima)。将梯度下降用于这种线性回归,总会收敛到全局最优。
4.7 随机梯度下降( stochastic gradient descent)
上面的梯度下降算法每次计算梯度都需要遍历所有的样本点,这是因为梯度是 J(θ) 的导数,而 J(θ) 是需要考虑所有样本的误差和 ,这个方法问题就是,扩展性问题,当样本点很大的时候,基本就没法算了。所以接下来又提出了随机梯度下降算法(stochastic gradient descent )。随机梯度下降算法,每次迭代只是考虑让该样本点的 J(θ) 趋向最小,而不管其他的样本点,这样算法会很快,但是收敛的过程会比较曲折,整体效果上,大多数时候它只能接近局部最优解,而无法真正达到局部最优解。所以适合用于较大训练集的情况。
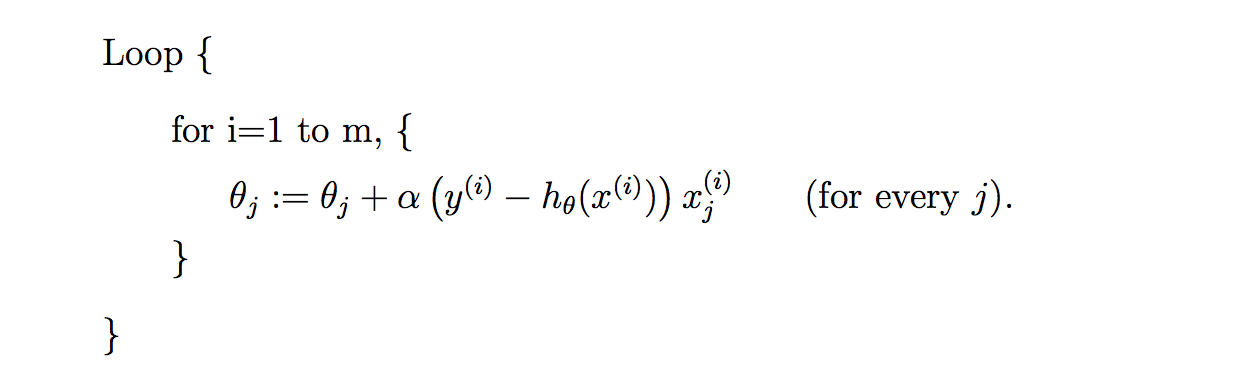
附:课后测试题答案
答案:D

这篇关于Coursera 机器学习(by Andrew Ng)课程学习笔记 Week 1——简单的线性回归模型和梯度下降的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





