学习笔记-李沐动手学深度学习（四）（12-13，权重衰退、L2正则化、Dropout）

本文主要是介绍学习笔记-李沐动手学深度学习（四）（12-13，权重衰退、L2正则化、Dropout），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

总结

【trick】过拟合及正则化项参数的理解

实际数据都有噪音，一般有噪音后，模型实际学习到的权重w就会比理论上w的最优解（即没有噪音时）大。（QA中讲的）

【好问题】
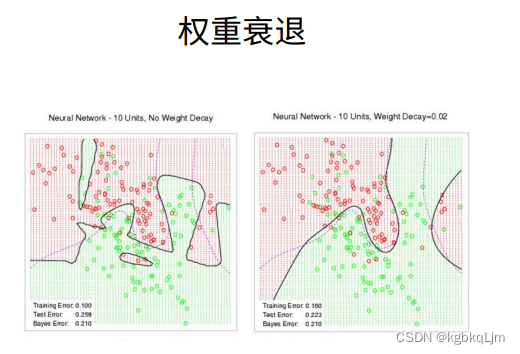
（1）不使用正则化（真正学习到的w=13 理论上的w=0.01，相差的还是很大）
（2）正则化权重lambd=3：明显已经减轻了过拟合的程度（但学到的w是0.3 还是比实际的w=0.01偏大的多）

因为实际上数据中有很多噪音，模型在学习时也会受他们的干扰，尝试去拟合噪音
实际的学习中是无法学习到理论上的最优解的（而且大概率实际学到的权重w很大），因为实际数据中有噪音，如果一点噪音没有，那么可能就不需要lambda了，因为你不会过拟合到一些奇怪的地方了

正则化与模型设计（模型复杂度）

可以将模型设计的复杂一点（如隐藏层多、每个隐藏层节点数多）+正则化来控制模型复杂度（如使用dropout并将其调大），
这样的效果会好于使用简单的模型+不用dropout的方式

12-权重衰退（weight decay，L2正则化）

【解决过拟合、实际效果不太大】
L2正则化也叫权重衰退、岭回归、Tikhonov正则，不同学术圈称呼不一样——《花书》

正则化项权重λ是控制模型复杂度的超参数
在这里插入图片描述

正则

通过正则的方式，可以使你的模型权重取值范围不会太大，以避免一定的过拟合

概述

L2范数

【L2范数】||w|| 或 ||w||₂ 。注：省略右下角角标2是指 L2范数是默认的范数。即一般说范数，就指L2范数
在这里插入图片描述
【各种范数参考链接】https://blog.csdn.net/weixin_58045467/article/details/131091687

本节用的是L2范数的平方
在这里插入图片描述

【引言理解】基于均方范数（L2）作为硬性限制

① 权重衰退是常见的处理过拟合的一种方法。
② 把模型容量控制比较小有两种方法，方法一：模型控制的比较小，使得模型中参数比较少。方法二：控制参数选择范围来控制参数容量。

③ 【基于θ控制w的范围】如下图所示，l为损失，在最小化损失时加入一个限制，即w向量中每一个元素的平方和小于一个特定值θ（即w向量中每一个元素的值都小于θ的根号），则 θ小 w的每一项就很小。
θ越小，对 w的L2范数限制就更强，极端情况就是θ=0，则只剩下偏移b了。（如 = 0.01，0.1，1）

④ 约束就是正则项。每个特征的权重都大会导致模型复杂，从而导致过拟合。控制权重矩阵范数可以使得减少一些特征的权重，甚至使他们权重为0，从而导致模型简单，减轻过拟合。

在这里插入图片描述

【正文】基于均方范数作为柔性限制

常用下图中的函数：（上图只是为了给大家更好的直观理解，即通过θ确实能限制w的范围）
【通俗理解】拟合得好就奖励，拟合不好有惩罚
λ是一个平滑的，不像上图红框这样的硬性限制。
w*： w的最优解
在这里插入图片描述

权重参数取值范围与模型复杂度关系理解

如果通过各种手段（如本节的L2范数即罚项即正则项权重）只是限制模型参数（如权重w）的取值的选择范围小，那么模型容量就小了
即如果不限制，那么 w取值范围很大，模型的权重w可以变化的很大、不柔和，那么理论上可以变成各种模型（即曲线的变化可能幅度很大），那么模型复杂度就可能很大。但如果w范围很小，那么能学出的模型的类型就会比较少，模型不复杂，你只能学出比较简单的模型
【简单来说就是如果一个多项式中的高次项的系数变小了，函数也就变平滑了】

演示与理解

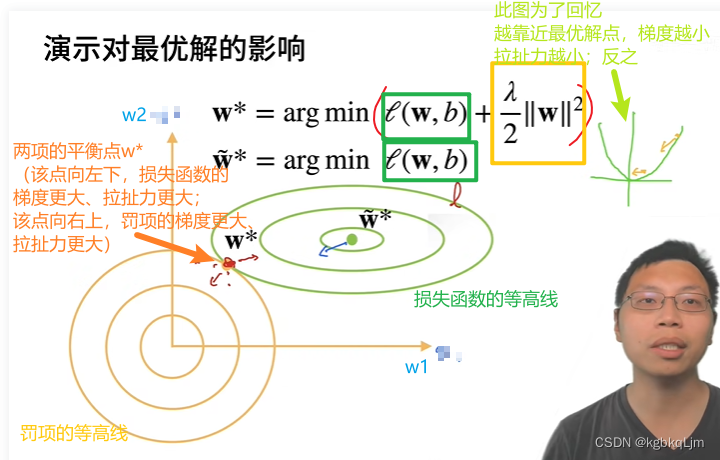
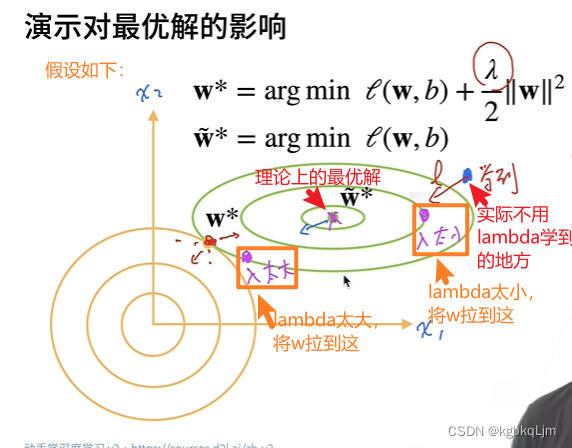
（弹幕说）绿线的中心点是最优解，也就是argmin loss，如果没有WD，会一直向绿线靠拢，w范数增加，而要让WD也变小的话，需要一直向原点靠拢，w范数要将小，这样就形成了拉扯，能够很好的应付过拟合。
WD：指权重衰退 weight decay

【下图说明】
下图中：横纵坐标为w向量的两个元素（即w1和w2）（假设L是一个二次函数，新引入的罚项也是一个二次函数）
绿线：损失L的等高线。如果想只优化损失L，则最优解在绿线中心即 w~（在此处 L的梯度为0）
黄线：假设罚项（黄框）是个二次函数，则该二次函数的等高线为黄色线
（弹幕说：等高线就是地理上的等高线这里应该叫等值线，即loss_func的值在这一条线（圈）上loss相等，联想一下低维loss_func的实际图像，这个只不过是把那个从上方拍扁）
w：相当于损失函数等高线和罚函数等高线的平衡点，
【体会】回想之前的损失函数与梯度，当平方损失函数离原点越远、梯度越大、向原点的拉扯力就越大，当离原点越近、梯度越小、拉扯力就越小

【整体上理解柔性引入罚项对损失的影响】罚项的引入，使得原损失函数（绿线）的最优解向原点靠拢了（从下图中 w~* => w*），那么 w1、w2的值都变小了，从模型复杂度的数值角度来说，模型复杂度变小了（因为衡量模型容量、模型复杂度有两个因素：参数数量和参数值的取值范围，此处相当于参数取值范围变小了）
在这里插入图片描述

参数更新法则

【权重衰退】每次计算梯度时，先把当前权重（如w_t）减小，然后再去计算梯度
w_t+1和之前梯度公式没有本质区别，只是每次 w_t先乘以一个小于1的正数，会变小一点
在这里插入图片描述

代码

从零实现

本节中罚项就写在了目标函数（即损失函数中）
在这里插入图片描述

在这里插入图片描述
线性回归问题，b为0.05，w为0.01，xi是随机的输入，最后是噪音

在这里插入图片描述

在这里插入图片描述
效果图：
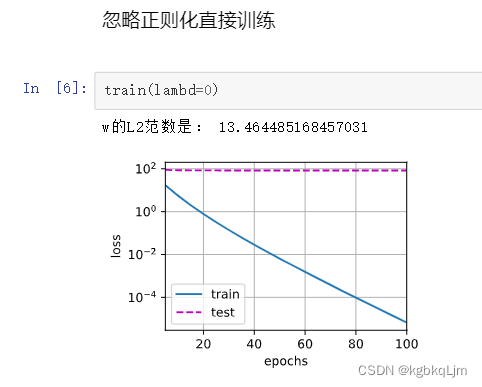
（1）不使用正则化（真正学习到的w=13 理论上的w=0.01，相差的还是很大）
明显是过拟合了，因为在训练误差一直在减小，但是测试集（严格来说即之前讲的验证集）上的误差不变，二者之间的差距一直在扩大
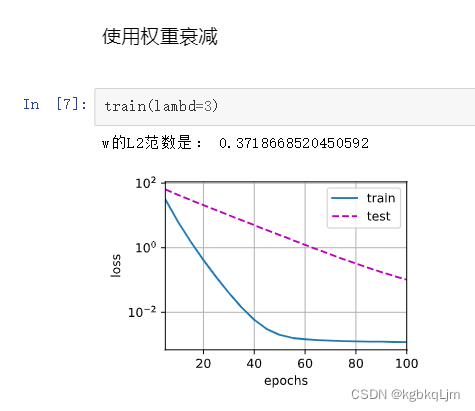
在这里插入图片描述
（2）正则化权重lambd=3：明显已经减轻了过拟合的程度（但学到的w是0.3 还是比实际的w=0.01偏大的多），但只是因为数据集太小了，100个epoch没完全解决过拟合。
也可以通过调大lambda来减小w

%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l
# 数据越简单，模型越复杂，越容易过拟合。四个参数分别为训练样本数、测试样本数、特征维度（特征向量中有多少种特征）
n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5 
true_w, true_b = torch.ones((num_inputs,1)) * 0.01, 0.05 # 真实的w和b
train_data = d2l.synthetic_data(true_w, true_b, n_train) # 生成人工数据集
train_iter = d2l.load_array(train_data, batch_size)  # 读取数组
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)# 初始化模型参数
def init_params():w = torch.normal(0,1,size=(num_inputs,1),requires_grad=True)  # 均值为0、方差为1、长度为200的向量b = torch.zeros(1,requires_grad=True)return [w,b]# 【本节核心】定义L2范数惩罚
def l2_penalty(w):return torch.sum(w.pow(2)) / 2# 定义训练函数
def train(lambd):  # 正则化权重项lambda（用lambd是想 和python关键字lambda区分）w, b = init_params()net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss  # 上面圈2定义的线性回归公式（python匿名函数、函数式编程？）num_epochs, lr = 100, 0.003animator = d2l.Animator(xlabel='epoch',ylabel='loss',yscale='log',xlim=[5,num_epochs],legend=['train','test'])  # 动画# 标准的训练过程for epoch in range(num_epochs):for X, y in train_iter:#with torch.enable_grad():l = loss(net(X),y) + lambd * l2_penalty(w)  # 与之前唯一的区别（引入了 罚项）l.sum().backward()d2l.sgd([w,b],lr,batch_size)if(epoch+1) % 5 == 0:if(epoch+1) % 5 ==0:animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss), d2l.evaluate_loss(net,test_iter,loss)))print('w的L2范数是',torch.norm(w).item())

基于框架实现

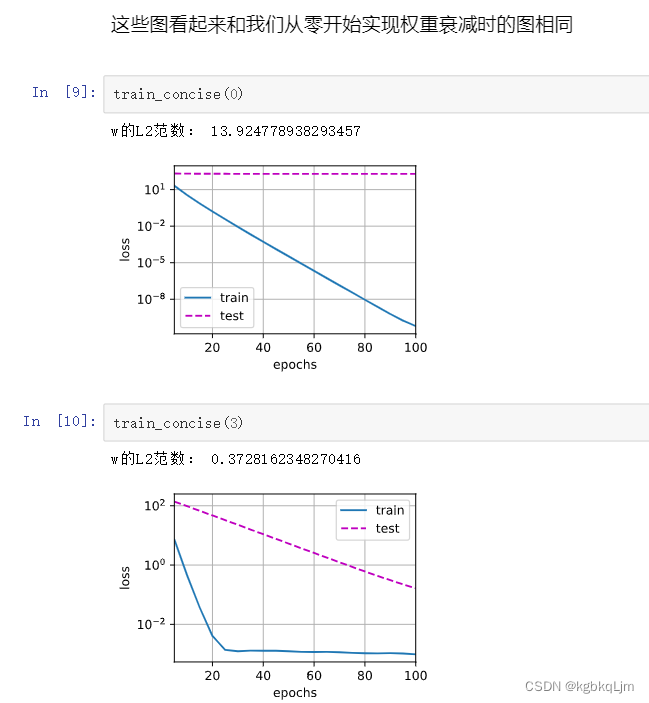
本节中罚项（即 lambda相关的）就写在了 pytorch提供的sgd接口中的 weight decay参数中，和从零实现的那种写法的效果一样

弹幕说：简洁实现前面一直都这样方式呀 1.建立网络 2. 损失函数 3. 优化器（根据反向传播求得梯度用优化器更具体都来更新参数） 4. 从训练集取出数据，进行训练，先梯度清0，算损失，反向传播，然后优化
在这里插入图片描述

# 简洁实现
def train_concise(wd):net = nn.Sequential(nn.Linear(num_inputs,1))for param in net.parameters():param.data.normal_()loss = nn.MSELoss()num_epochs, lr = 100, 0.003# 【与之前的唯一区别】惩罚项既可以写在目标函数里面（如上一节的从零实现），也可以写在训练算法里面（如此处），每一次在更新之前把当前的w乘以衰退因子weight_decay    trainer = torch.optim.SGD([{"params":net[0].weight,"weight_decay":wd},{"params":net[0].bias}],lr=lr)                  animator = d2l.Animator(xlabel='epoch',ylabel='loss',yscale='log',xlim=[5,num_epochs],legend=['train','test'])                   for epoch in range(num_epochs):for X, y in train_iter:with torch.enable_grad():trainer.zero_grad()l = loss(net(X),y)l.backward()trainer.step()if(epoch + 1) % 5 == 0:animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss), d2l.evaluate_loss(net,test_iter,loss)))print('w的L2范数是',net[0].weight.norm().item())

QA

在这里插入图片描述
1.不支持
但可以将复数看成二维，用二维数据来实现

2.只是限制模型参数（如权重w）的取值的选择范围小，那么模型容量就小了
即如果不限制，那么 w取值范围很大，模型的权重w可以变化的很大、不柔和，那么理论上可以变成各种模型（即曲线的变化可能幅度很大），那么模型复杂度就可能很大。但如果w范围很小，那么能学出的模型的类型就会比较少，模型不复杂，你只能学出比较简单的模型
【简单来说就是如果一个多项式中的高次项的系数变小了，函数也就变平滑了】

就改成这样

4.【权重衰减的值即 lambda】一般取 1e-3、1e-4
如果模型很复杂，权重衰退不会带来特别好的效果

【L2范数】||w|| 或 ||w||₂ 。注：省略右下角角标2是指 L2范数是默认的范数。即一般说范数，就指L2范数
在这里插入图片描述

本节用的是L2范数的平方

6.【好问题】
（1）不使用正则化（真正学习到的w=13 理论上的w=0.01，相差的还是很大）
（2）正则化权重lambd=3：明显已经减轻了过拟合的程度（但学到的w是0.3 还是比实际的w=0.01偏大的多）

在这里插入图片描述

7.不是让w变得更平均，即一般模型实际学到的w都是偏大的，即overfit的，此时用lambda可以往回拉w。但如果你的模型没学到overfit，往回拉也没用。

8.1e-2,1e-3,1e-4

9.lambda不会有特别大的用，会有一点点好处。
比如lambda=0，看下效果有多不好，再尝试 1e-3、1e-2等，看看有没有更好的效果

在这里插入图片描述

10.可以证明的，也可以自己试一下。
弹幕说：林轩田老师《机器学习基石》中有讲过

13-丢弃法（dropout）

比权重衰退效果好
现在认为drop是正则项（正则化）（之前一开始hinton提出dropout时认为就是每次随机丢弃一些权重后得到了子神经网络，最后对这些神经网络的结果取平均效果会更好，但现在一般认为 dropout是正则项）
在这里插入图片描述

理论

退学率：

在这里插入图片描述

引言

好的模型要有很好的鲁棒性

此处的噪音指随机的加噪音，与上一节的噪音不同（上节指固定噪音）
dropout：在层与层之间加噪音（从这个角度来看，dropout也是正则）

弹幕说：
因为随机扰动就不会让模型完全能拟合成输入数据的样子
Dropout 引入的噪音与常规的数据噪声不同。因为是随机加入，这种“强制学习”让模型更加鲁棒，更能够关注整体特征而非局部模式
在这里插入图片描述

【Dropout定义】无偏差的加入噪音

【基本理解】dropout是正则化的一种方式
【dropout作用场景】
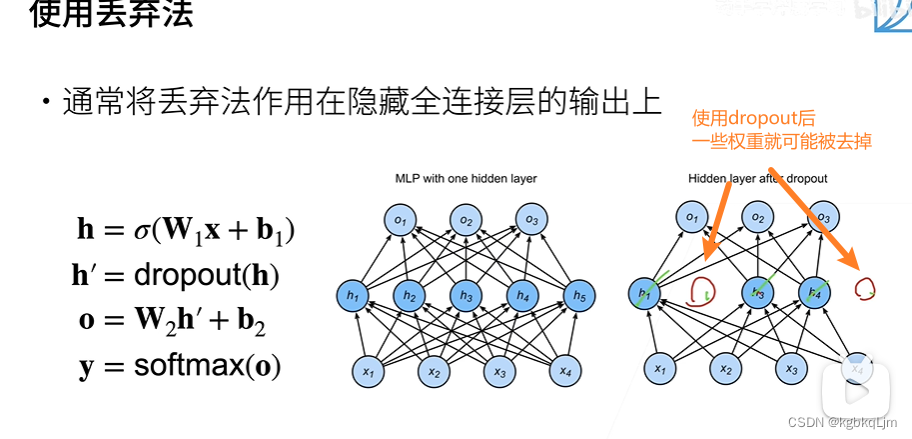
（1）位置：一般应用在全连接的隐藏层的输出上（不会作用于卷积层）
（2）时间：且只作用在训练过程中，不作用于预测时（具体是每一个layer在调用forward进行前向计算时随机丢弃一次）
（即训练时会在每一个forward时，随机丢弃掉一些神经元在这一个forward时不参加计算和更新，但是在预测时是所有的神经元都参加）

【概率p】丢弃概率（如本节中的p）是控制模型复杂度的超参数（一般取0.1、0.5、0.9）

下图中x指一层到下一层之间的输出
E[x’]=x：其中E[x’]指x‘的期望。即希望虽然对x引入了噪音变成了x’，但 x’的期望（即平均下来）还是等于原x
p为概率，x_i为输入x（是向量）的第i个元素
对于x经扰动计算后的结果x’：（一定概率上将x变为0，一定概率上将x变大）
（1）在概率p下将输入变为0；
（2）其他情况下将输入x变大得到x’
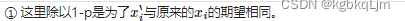
在这里插入图片描述

在这里插入图片描述

【训练过程中】使用dropout

假设神经网络是如下图的单隐藏层：
h为第一个隐藏层的输出
在这里插入图片描述

【预测过程中】使用dropout

推理（即预测）中是不需要正则（即此处的dropout的），因为预测时不需要权重发生变化
即推理时 dropout不改变输入h，直接得到输出h
在这里插入图片描述

代码实现

从零实现

在这里插入图片描述

在这里插入图片描述
【精髓】每次调用该函数时，输入的向量中的元素有50%概率被置为0（即被丢掉）

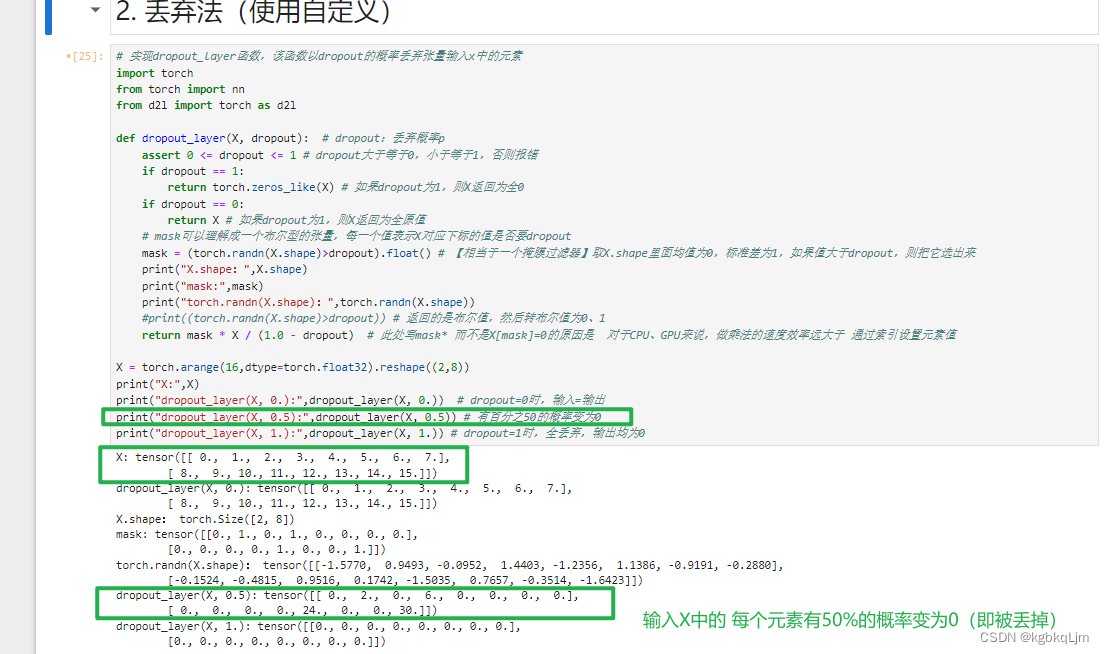
# 实现dropout_layer函数，该函数以dropout的概率丢弃张量输入x中的元素
import torch
from torch import nn
from d2l import torch as d2ldef dropout_layer(X, dropout):  # dropout：丢弃概率passert 0 <= dropout <= 1 # dropout大于等于0，小于等于1，否则报错if dropout == 1:return torch.zeros_like(X) # 如果dropout为1，则X返回为全0if dropout == 0:return X # 如果dropout为1，则X返回为全原值# mask可以理解成一个布尔型的张量，每一个值表示X对应下标的值是否要dropoutmask = (torch.randn(X.shape)>dropout).float() # 【相当于一个掩膜过滤器】取X.shape里面均值为0，标准差为1，如果值大于dropout，则把它选出来print("X.shape：",X.shape)print("mask:",mask)print("torch.randn(X.shape)：",torch.randn(X.shape))#print((torch.randn(X.shape)>dropout)) # 返回的是布尔值，然后转布尔值为0、1return mask * X / (1.0 - dropout)  # 此处写mask* 而不是X[mask]=0的原因是  对于CPU、GPU来说，做乘法的速度效率远大于 通过索引设置元素值X = torch.arange(16,dtype=torch.float32).reshape((2,8))
print("X:",X)
print("dropout_layer(X, 0.):",dropout_layer(X, 0.))  # dropout=0时，输入=输出
print("dropout_layer(X, 0.5):",dropout_layer(X, 0.5)) # 有百分之50的概率变为0
print("dropout_layer(X, 1.):",dropout_layer(X, 1.)) # dropout=1时，全丢弃，输出均为0

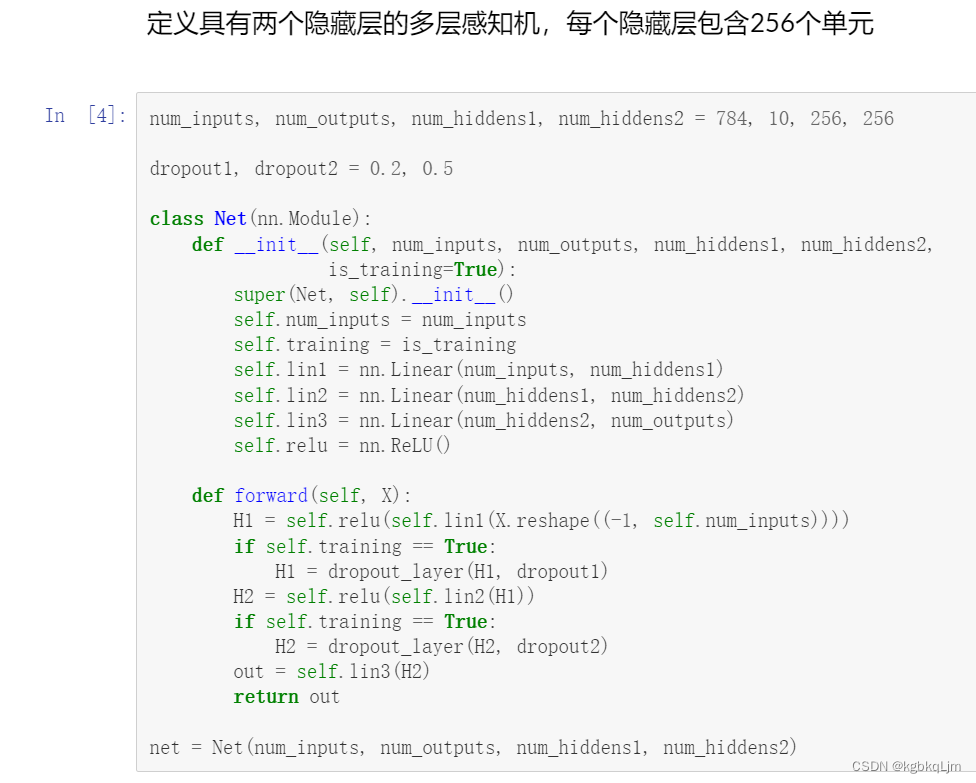
【定义具有两个隐藏层的多层感知机，每个隐藏层包含256个单元】

# 定义具有两个隐藏层的多层感知机，每个隐藏层包含256个单元
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10 ,256, 256dropout1, dropout2 = 0.2, 0.5class Net(nn.Module):def __init__(self, num_inputs, num_outputs, num_hiddens1, num_hiddens2,is_training=True):       super(Net, self).__init__()self.num_inputs = num_inputsself.training = is_trainingself.lin1 = nn.Linear(num_inputs, num_hiddens1)self.lin2 = nn.Linear(num_hiddens1, num_hiddens2)self.lin3 = nn.Linear(num_hiddens2, num_outputs)self.relu = nn.ReLU()def forward(self, X):H1 = self.relu(self.lin1(X.reshape((-1,self.num_inputs))))if self.training == True: # 如果是在训练，则作用dropout，否则则不作用H1 = dropout_layer(H1, dropout1)H2 = self.relu(self.lin2(H1))if self.training == True:H2 = dropout_layer(H2,dropout2)out = self.lin3(H2) # 输出层不作用dropoutreturn outnet = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)# 训练和测试
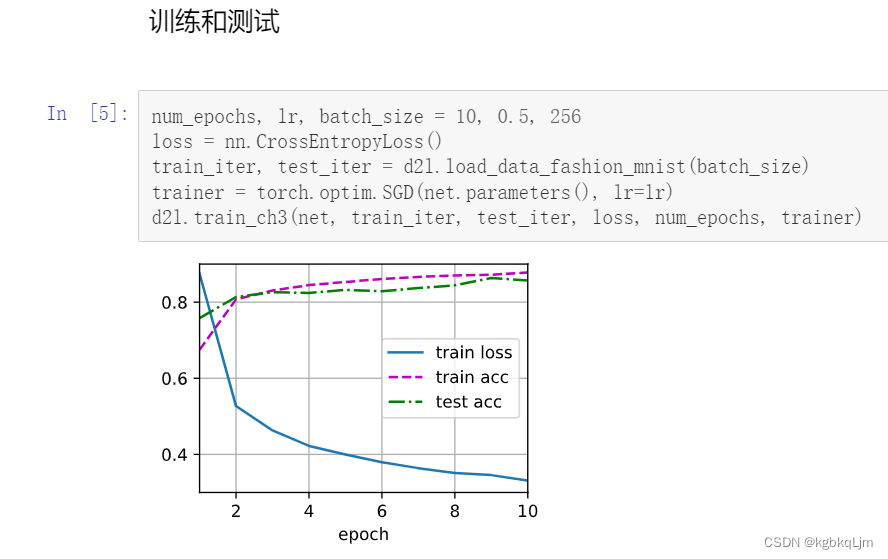
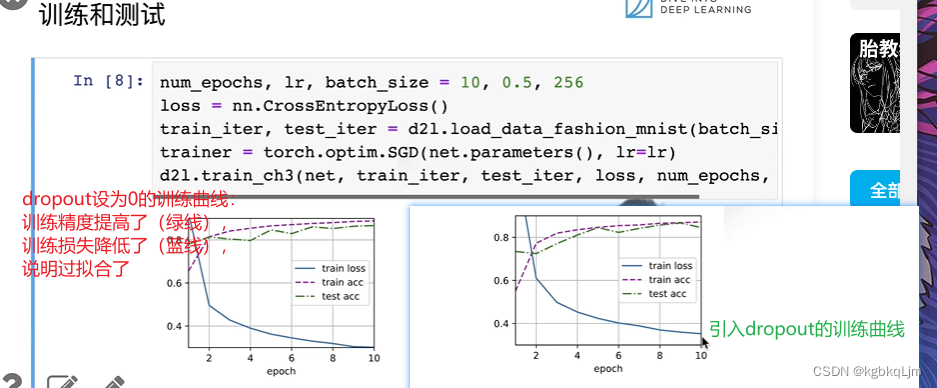
num_epochs, lr, batch_size = 10, 0.5, 256
loss = nn.CrossEntropyLoss()
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = torch.optim.SGD(net.parameters(),lr=lr)
d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,trainer)

在这里插入图片描述

基于框架实现

在这里插入图片描述

import torch
from torch import nn
from d2l import torch as d2l# 简洁实现
num_epochs, lr, batch_size = 10, 0.5, 256
dropout1, dropout2 = 0.2, 0.5
loss = nn.CrossEntropyLoss()
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)net = nn.Sequential(nn.Flatten(),nn.Linear(784,256),nn.ReLU(),nn.Dropout(dropout1),nn.Linear(256,256),nn.ReLU(),nn.Dropout(dropout2),nn.Linear(256,10))def init_weights(m):if type(m) == nn.Linear:nn.init.normal_(m.weight,std=0.01)net.apply(init_weights)trainer = torch.optim.SGD(net.parameters(),lr=lr)
d2l.train_ch3(net,train_iter, test_iter, loss, num_epochs,trainer)