本文主要是介绍【MATLAB源码-第126期】基于matlab的樽海鞘算法(SSA)机器人栅格路径规划,输出做短路径图和适应度曲线。,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
操作环境:
MATLAB 2022a
1、算法描述
樽海鞘算法(Salp Swarm Algorithm, SSA)
樽海鞘算法是一种基于群体智能的优化算法,它通过模拟樽海鞘在海洋中的社会行为来解决优化问题。这种算法的设计灵感来源于樽海鞘的群体行为,尤其是它们在觅食时的协同行动方式。
背景
樽海鞘是一类海洋生物,属于脊索动物门。它们以群体的形式生活在海洋中,通过协调的方式进行觅食和移动。在自然界中,樽海鞘群体的行为表现出极高的组织性和效率,这使得它们成为算法设计的良好借鉴对象。
算法灵感
樽海鞘算法的设计灵感主要来自于两个方面:一是樽海鞘的群体结构,二是它们的觅食行为。在自然界中,樽海鞘群体中的个体通过协作与信息共享,共同寻找食物资源,这种行为在算法中被抽象为寻找最优解的过程。
算法结构
樽海鞘算法将群体分为两部分:领头者和追随者。领头者负责引导整个群体,而追随者则根据领头者和其他追随者的位置来调整自己的位置。
1. 领头者(Leader)
领头者在算法中代表当前找到的最优解。它的位置是根据问题的目标函数来更新的。在每次迭代中,领头者根据目标函数的反馈调整自己的位置,引导群体向着更优的区域移动。
2. 追随者(Followers)
追随者的任务是探索解空间,以寻找可能的更优解。它们的位置更新依赖于领头者的位置以及其他追随者的位置。这种机制确保了群体能够在广阔的解空间中进行有效搜索。
位置更新规则
樽海鞘算法中的关键是位置更新规则。这个规则决定了算法如何探索解空间,并最终找到最优解。
1. 领头者更新规则:领头者根据目标函数的梯度或者其他启发式信息更新其位置。这反映了在实际觅食中,樽海鞘会根据环境的变化调整移动方向。
2. **追随者更新规则:追随者的位置更新则更加复杂,它不仅依赖于领头者的位置,也受到其他追随者位置的影响。这种更新机制模拟了樽海鞘群体中的信息传递和个体间的相互作用。
觅食行为的模拟
樽海鞘算法通过模拟樽海鞘的觅食行为来搜索最优解。在自然界中,樽海鞘群体在寻找食物时会表现出高度的协同和效率,这在算法中体现为快速而有效地搜索解空间。
1. 探索与开发:算法平衡了探索(Exploration)和开发(Exploitation)两个方面。探索指的是搜索新的区域,而开发则是在已知的有希望区域进行深入搜索。
2. 动态调整:樽海鞘算法能够根据当前搜索情况动态调整探索与开发的比重,这使得算法在不同的搜索阶段都能保持高效。
应用范围
樽海鞘算法由于其独特的优化机制和高效的搜索能力,已被广泛应用于多个领域,如工程优化、路径规划、资源分配、机器学习等。
算法优势
1. 高效的全局搜索能力:算法能够在较大的解空间中有效地搜索全局最优解。
2. 良好的适应性:樽海鞘算法可以适应各种类型的优化问题。
3. 简洁易实现:相对于其他优化算法,樽海鞘算法在实现上更为简洁直观。
面临的挑战
尽管樽海鞘算法在多个方面表现出色,但在实际应用中仍面临一些挑战,如局部最优解的问题、参数调整的敏感性等。
未来发展
未来,随着对樽海鞘算法的深入研究和应用领域的拓展,其在解决复杂优化问题中的作用将越来越大。同时,结合其他优化算法的优点,对樽海鞘算法进行改进和优化也是研究的重要方向。
结论
樽海鞘算法作为一种新兴的群体智能优化方法,其在解决实际问题方面展现的潜力令人瞩目。随着技术的不断发展和完善,它将在各种优化问题中发挥更加重要的作用。
2、仿真结果演示

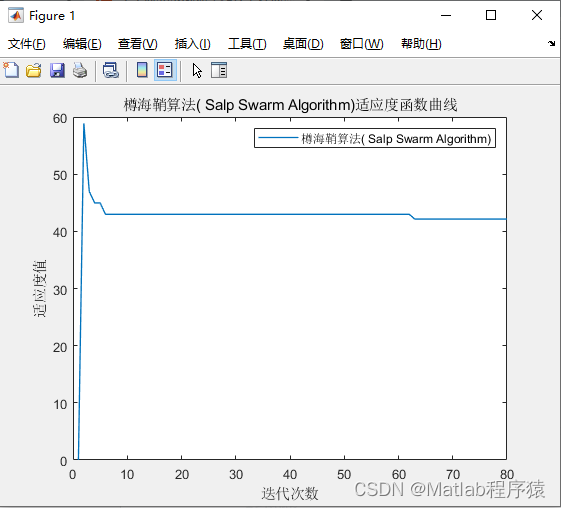
3、关键代码展示
l=略
4、MATLAB 源码获取
V
点击下方名片
这篇关于【MATLAB源码-第126期】基于matlab的樽海鞘算法(SSA)机器人栅格路径规划,输出做短路径图和适应度曲线。的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









