Planning for electric vehicle needs by coupling charging profiles with urban mobility

这是发表在nature energy上的一篇论文，相当牛的期刊，相当牛的论文，花了两天看了下，在此就慢慢解读记录下。

1.文章概述

论文主要是分析了电动汽车充电问题，也就是说现在电动车越来越多，这些电动车一起充电，将会带来一个用电高峰，这个高峰可能会使得区域供电系统不稳定，甚至崩溃，因此作者希望能够降低峰值用电情况，解决这个问题的办法很自然地想到是错峰用电，这样就可以减小用电峰值了，但是如何错峰呢？作者提出可以让出行者提早一点到或延迟一点到，这里提早或延迟是很小的，比如10min，通过这样的调整，期望使得用电高峰大幅降低，同时又不对出行者的出行行为造成较大干扰。为了解决这个优化问题，作者同时使用了手机信令数据分析出行模式、充电数据分析充电行为、问卷调查数据和普查数据调查电动车和非电动车出行行为差异。把这些结合起来，完成了该优化问题。
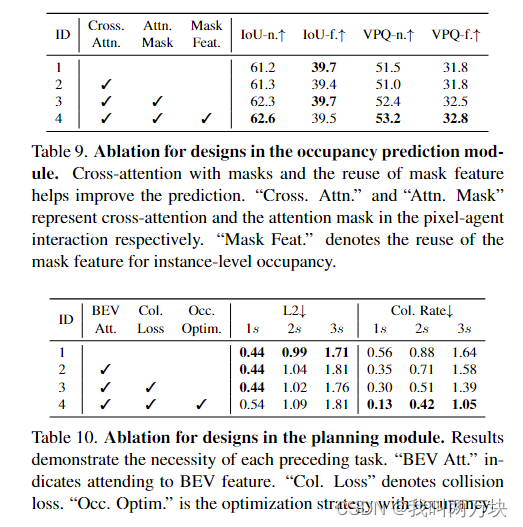
具体而言，第一部分作者基于手机信令数据分析出行行为模式；第二部分基于问卷数据和手机信令数据识别路网上的电动车辆；第三部分使用充电数据分析了充电行为、充电需求、并对仿真做了标定；第四部分解决了上述的优化问题，可以参考下图。

2.基于手机信令数据的出行行为分析

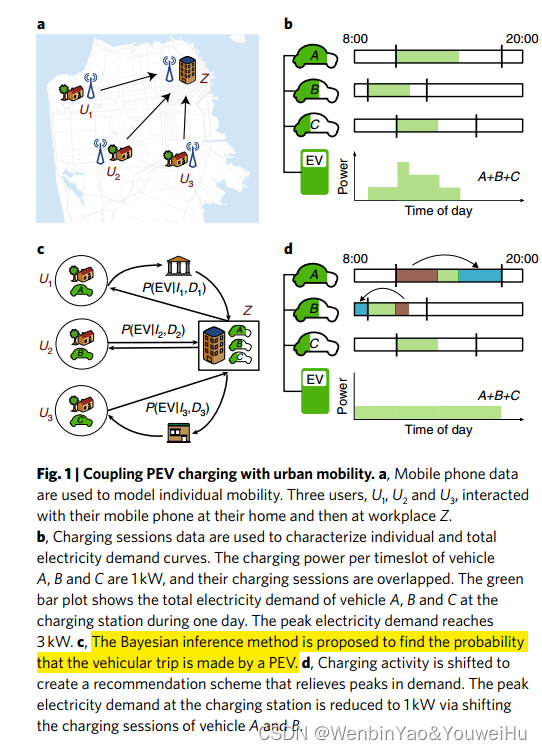
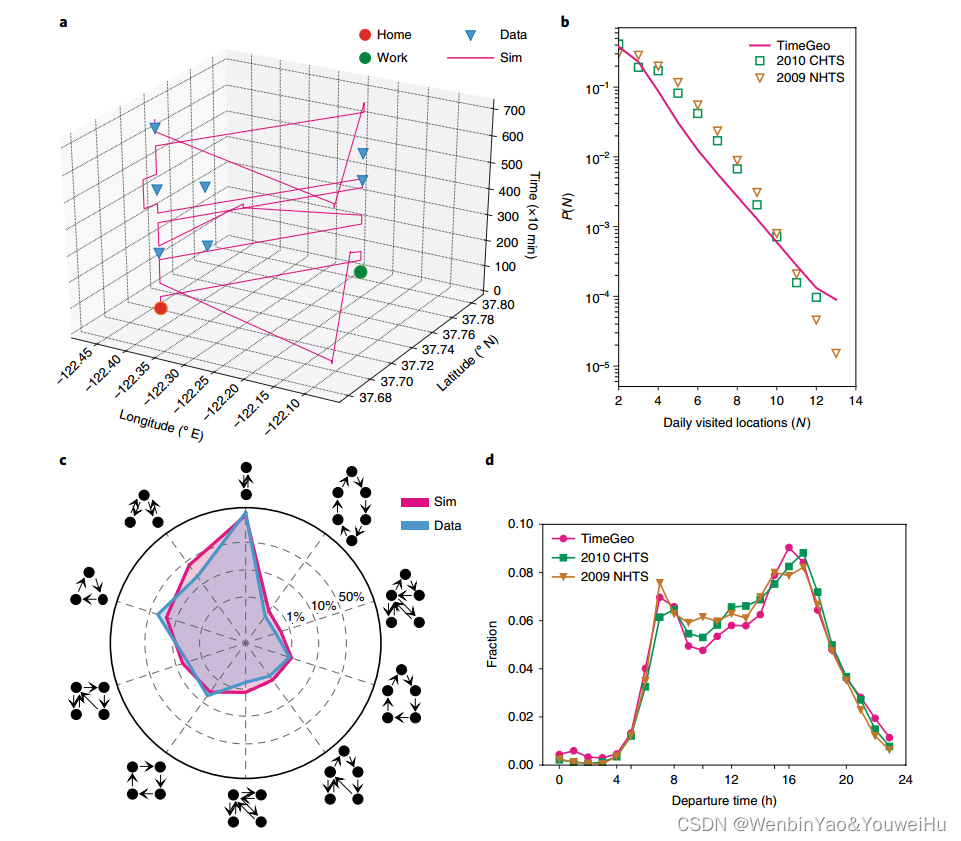
作者首先提取驻足点，然后基于驻足点识别出每个出行者的家和工作地，根据是否有工作地把出行者分为通勤出行者和非通勤出行者。然后使用TimeGeo这个模型来对整个城市的所有出行者进行行为仿真，TimeGeo这个模型主要由两部分构成，第一部分是时间维度选择，第二部分是空间维度选择，时间维度选择指首先将一天离散化，然后判断出行者在下一个时间步是否会移动，空间维度选择指判断出行者在下一个时间步是否会移动去一个新的地方。借助该模型对一个城市所有的出行者进行仿真分析，得到每个出行者的出行模式。仿真结束后必然的一步是对检验仿真效果，作者使用城市宏观的出行调查指标验证，发现仿真和真实情况吻合很好。下图的图a是timeGeo模型的仿真数据和真实数据，图b、c、d都是在验证仿真结果是否可以和真实结果相吻合。注意这边出行行为实际上知道每个时间步的轨迹了，当然同时也知道motif了。

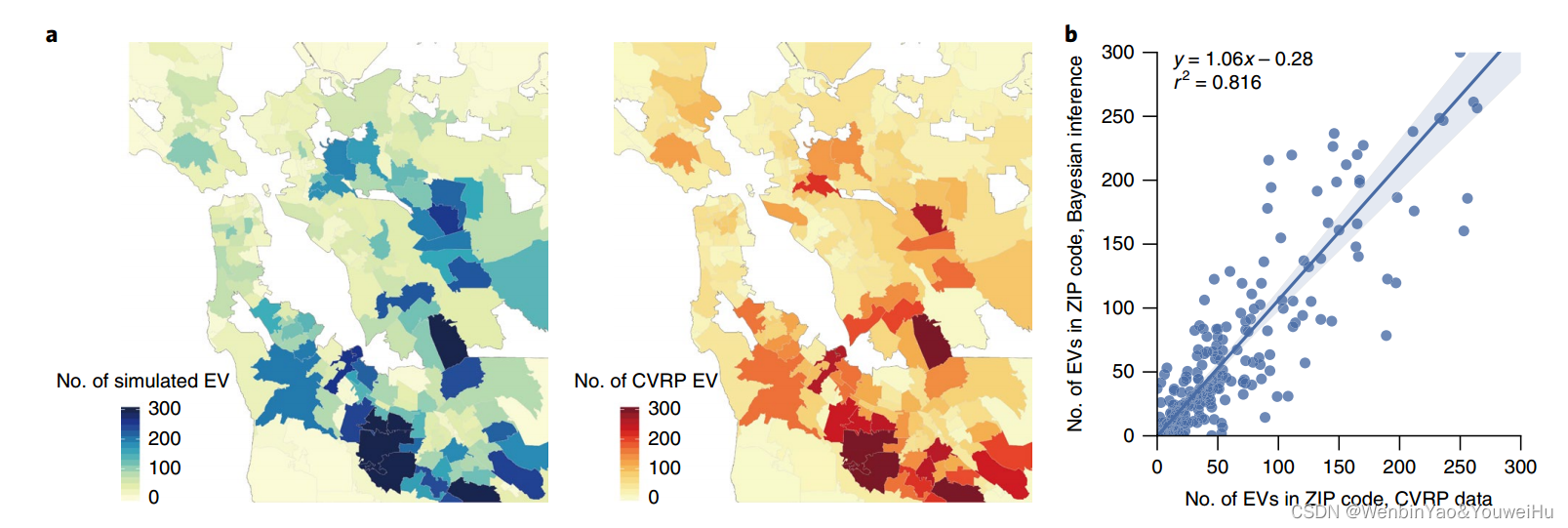
在得到出行者的仿真出行数据后，作者期望分析每位出行者是使用电动汽车出行的概率，因为仿真数据虽然有每个人的出行时空轨迹了，但是不知道他到底是不是电动汽车出行的。为了实现这个，作者借助机动车使用率首先提取出机动车出行的个体，然后基于这些个体的收入和每日出行距离用贝叶斯方法识别出个体使用电动汽车出行的概率。这里有一点需要说明下，这里提到的个体收入并不是真的有个体收入数据，而是普查数据，再加上假定该区域人口的收入服从标准正态分布得到的，出行距离的话可以通过前面仿真结果得到。这些有了后面的贝叶斯预测就很简单了，无非是一个机器学习模型而已，用问卷数据去训练，然后对整个样本去做预测即可了。当然作者可以这样做的原因也是因为他基于问卷数据的分析发现电动车和燃油车出行距离和收入水平是有差距的，因此认为用这两个feature可以识别出电动车使用者，这个预测个体层面而言肯定是不准的，但是宏观层面来讲，可以认为是准的。当然作者也检验了从宏观统计而言，这个贝叶斯预测电动汽车使用者是否准确。此外，作者也分析了一下电动车和非电动车的出行行为差异，以及这个差异和问卷调查结果是否一致。

3.电动汽车充电行为分析

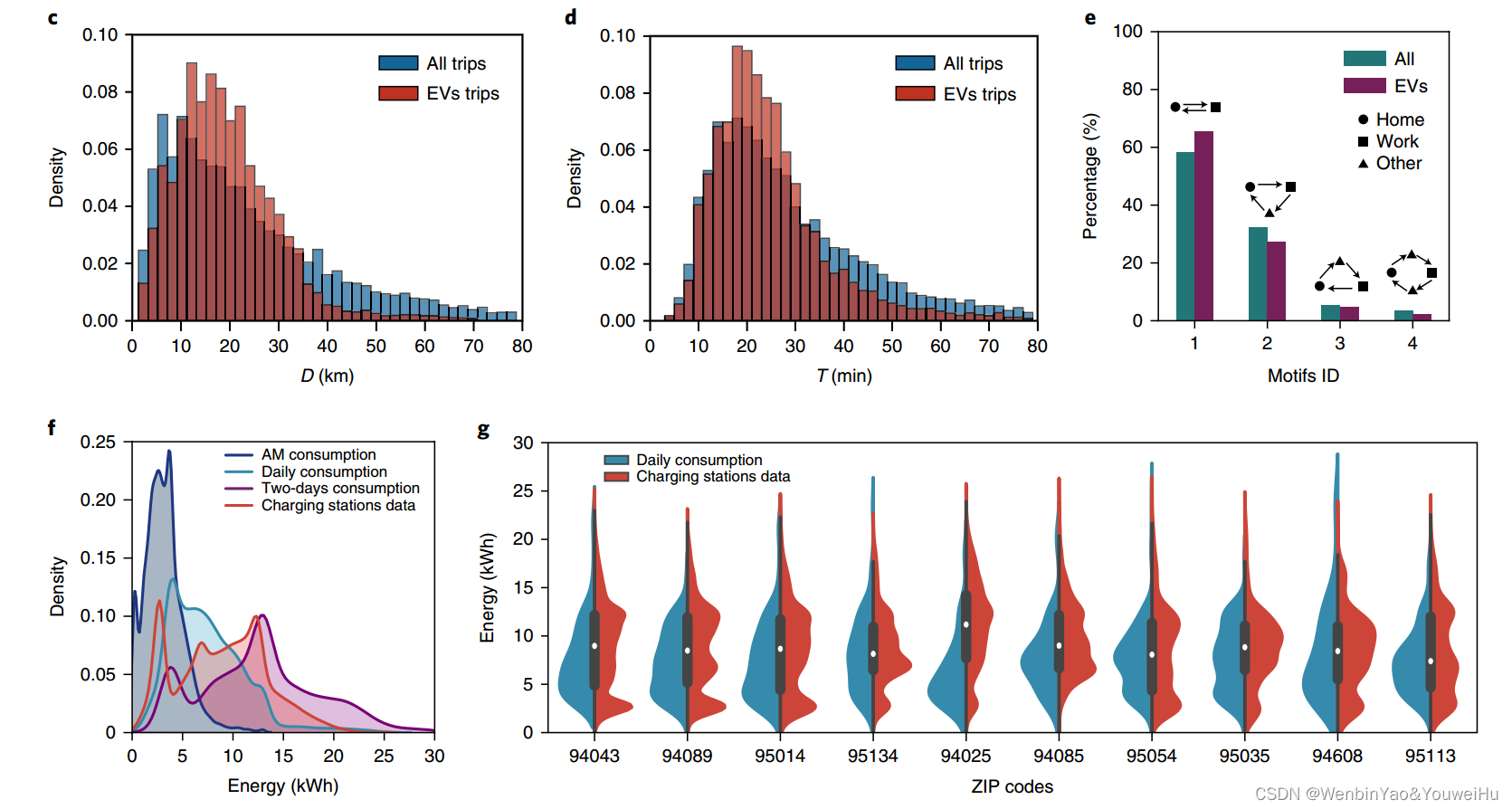
这部分主要进行了1.充电桩访问模式和采用率，2.车辆到达和离开的时间维度的特性，3.能源消耗情况分析。
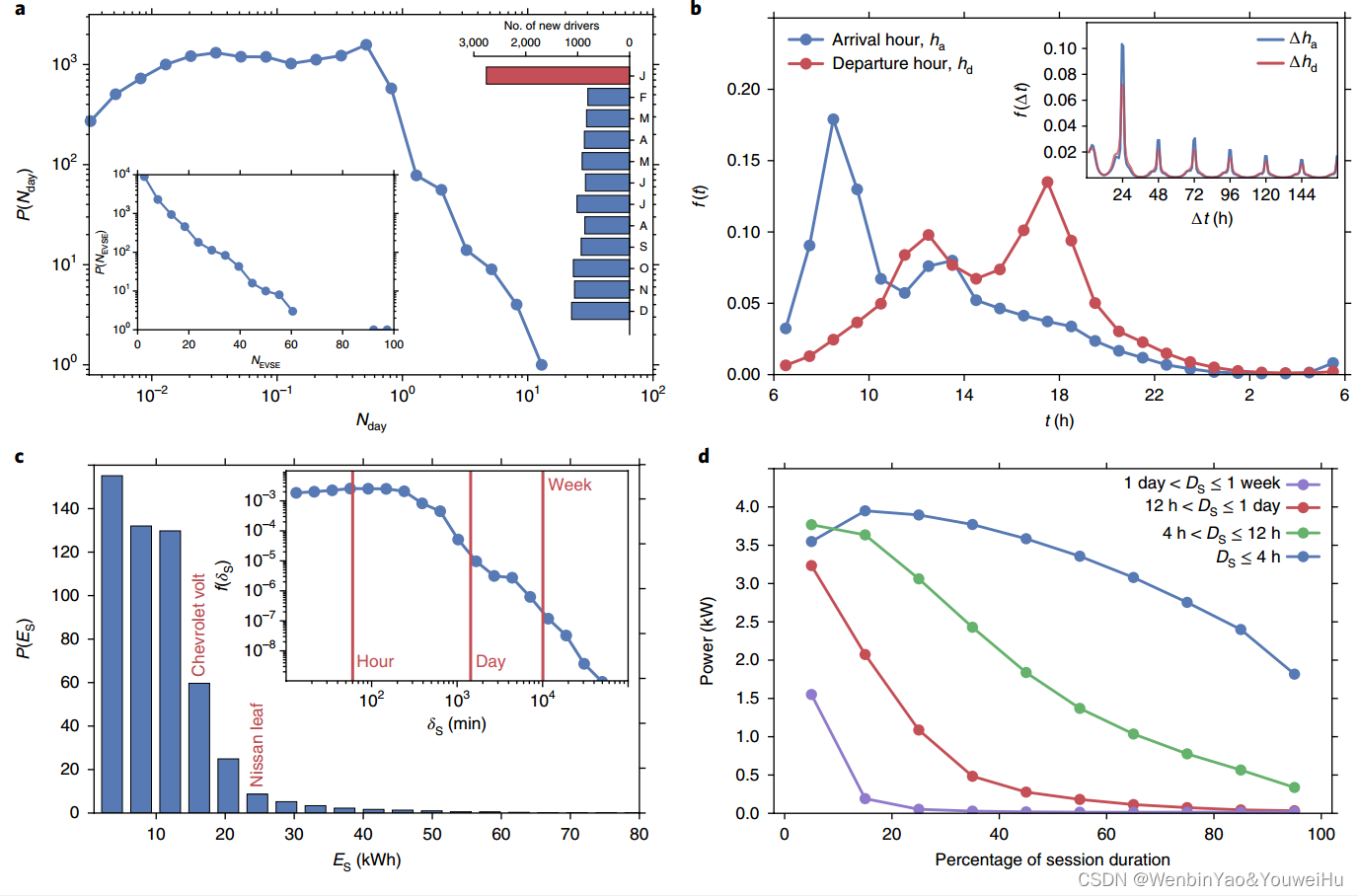
三块内容其实只需要看下面的四张图就可以完全知道了，图a是分析了平均每天的充电次数，发现大部分人平均每天充电次数小于1，图b主要分析充电开始和离开时间的分布情况，发现了早晚高峰充电需求分布，图c分析了平均每个充电桩的能源消耗情况，并标注了两种经典的电池容量大小，发现大部分人充一次电实际上是小于一次电池容量的，这说明很多人都是还有电的时候就去冲，或是也不充满就离开了。图d主要是将充电类型分成4种，分别是充电时间小于4小时，4-12h，12h-1天，大于1天小于一周，然后将四种充电类型分别绘制折线图，分析充电功率和充电持续时间的关系，充电功率大致可以分成三个等级：L1,L2,L3（120V,240V,480V）。有过电动车充电的人可能了解，充电是分成不同阶段的，刚开始是大功率快充，等到冲到一定程度可能功率下降，速度变慢，最后很小功率到充满，其实手机也是类似，作者其实就是分析充电时间和这种功率间的关系是咋样的。我们可以发现充电时间越短其实功率越大，这个也和我介绍的电池充电原理是一致的，作者就说这说明充电桩没有任何充电策略，就是车到了就充电，这个也是没问题的。

4.出行模式以及能源需求结合分析

这部分主要基于个人出行模式分析了能源需求。作者通过充电桩数据分析了电力需求分布、通过电动车出行模式分析了电力需求分布。
为了通过出行模式分析电力需求分布，作者将电动车出行能源消耗划分为四种类别，分别是drivetrain model for the two battery electric vehicle (BEV) modes, Nissan Leaf and Tesla Model S， the charge-depleting model for the two plug-in hybrid electric vehicle (PHEV) modes, Chevrolet Volt and Toyota Prius（这块和电动汽车有关，我也不是特别理解了），对于某种特定模式，基于平均速度和平均距离来评估能源消耗。
由于充电数据的粒度不够细，因此作者划分成这样3种充电情况来分析：上午消耗、每日消耗、两天消耗三种情况。这三种情况对应三种不同的出行行为，分别是每天同时在家和在工作地充电桩充电、一天在工作地充电一次、两天在工作地充电一次（两天的能源消耗等于充电一次的量）。
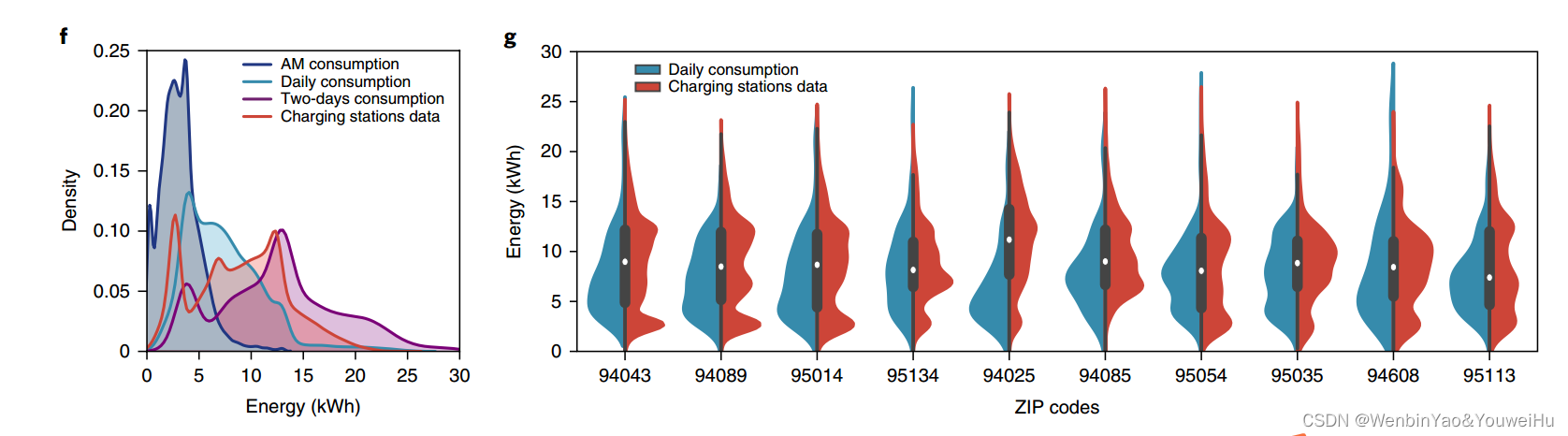
下图f比较了三种情况下的能源消耗情况，同时也绘制了真实数据的情况，下图g绘制了每日的能源消耗估计值和充电数据真实值的分布情况，真实值有更多明显的峰值，这可能源于充电行为的简化造成的。为了使得估计的充电行为和充电桩充电数据结果相匹配，作者调整了三种充电行为的占比，分别为10%, 35%和55%，这样的分配结果可以使得充电情况和真实数据匹配，并且和一份报告的比例也吻合。

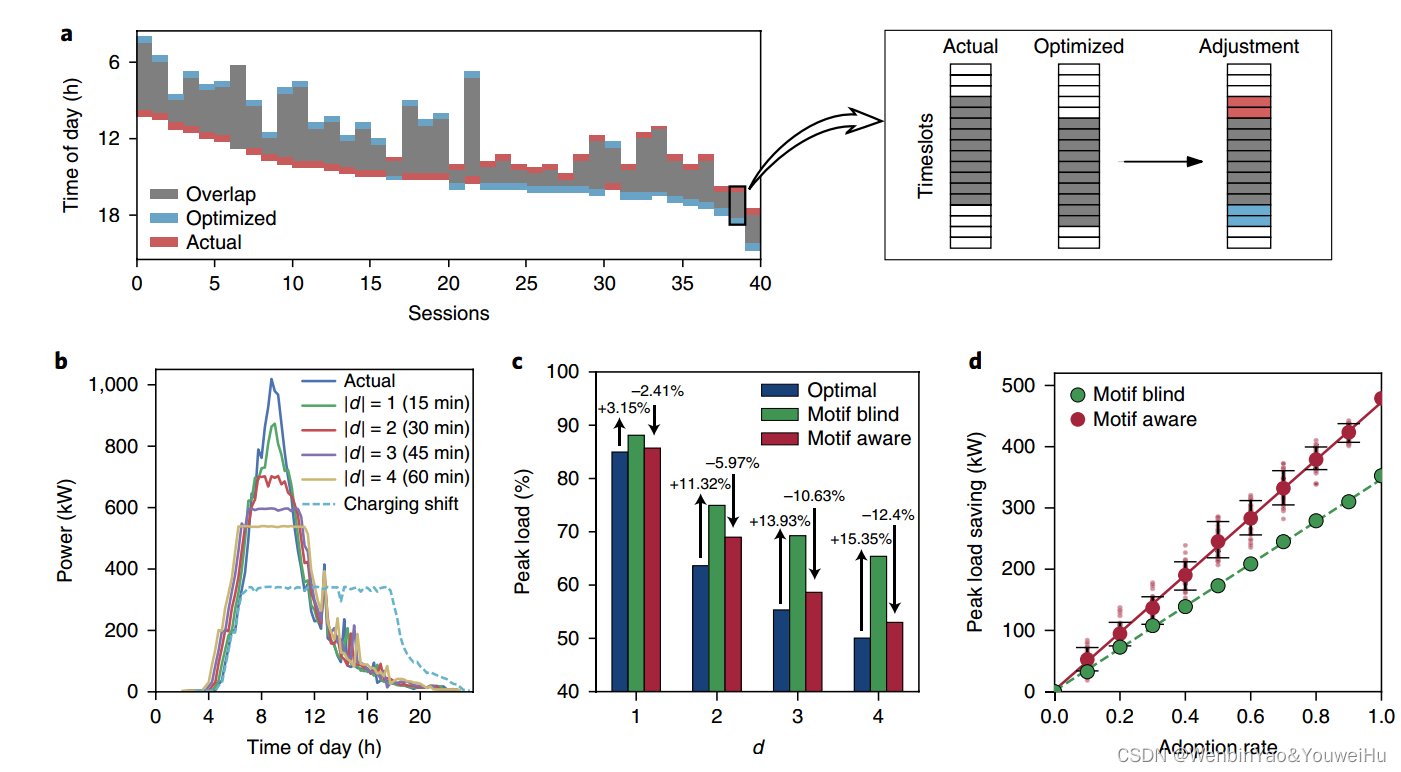
5.结合出行模式的缓解充电需求峰值策略分析

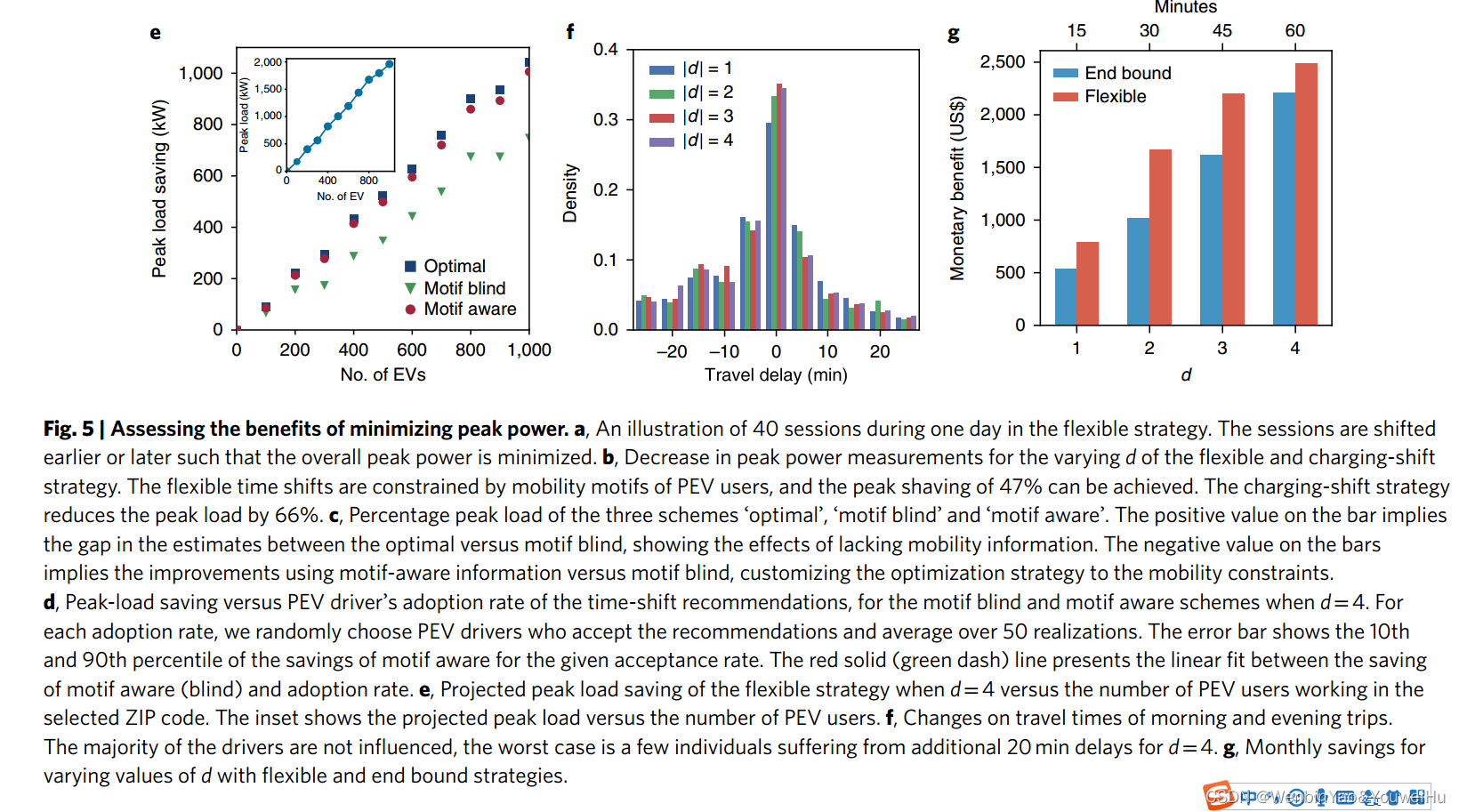
这一节也就是文章的重点了，作者希望通过调整出行者的充电时间来降低充电需求峰值（其实我感觉和限行或者诱导出行有异曲同工之妙）。这个问题毫无疑问是一个优化问题，具体而言，作者将该问题转化为了一个混合整数优化问题，优化的变量是车辆的到达时间和充电结束时间。作者提出了两种优化策略，第一种是作者固定了车辆的离开时间，但是允许调整到达时间，最多提前$d^i$到达，也就是到达时间的优化空间是[0,$d^i$]，这种策略作者称之为 end bound。第二种策略可以同时优化到达时间和离开时间，优化上限也是d，这种策略称之为flexible strategy。这两种策略都是在车辆一到达就充电的假设下进行的，除了这个作者也分析了如果充电时间可以自定义优化，效果将更好，也就是说比如车到了，先不充电，而是过会充电，当然这个前提是不影响车辆的离开。下面的图a分析了flexible strategy的优化情况，图b给出了不同的d下面的优化效果。在此基础上，作者还分析了考虑到出行约束时，优化情况是怎么样的，出行约束的含义是，出行者的motif已经知道了，有的人工作前或后还有其他事，如果有其他事的话，他就没法提前或延后到达或离开了，这个也就是出行约束，这个出行约束主要是考虑到不同出行行为的人对调整建议的接受率。对于Home-work-home的人，他可以接受提前或延后，对于home-work-other-home的人，他不能延迟离开，因为工作后还有其他事，对于home-other-work-home的人，他不能提前到达，对于home-other-workother-home的人，既无法提前到达也无法延迟离开。图c比较了是否考虑出行约束对优化结果的影响，图c中共有三种范式，分别是所有人都可以接受提前和延迟调整（optimal）、 the motif blind指如果优化变量不满足出行约束，那么他就不会接受这个建议的情况、the motif aware指基于个体出行模式给予自适应的优化策略的情况。这三种范式分别在end bound和 flexible schemes两种情况下都做了测试，但是这个结果放在附录里了，图c只给了flexible schemes的情况。图d给出了策略接受率和峰值能源消耗减小率之间的关系，近似是呈线性关系的。图e给出了峰值能源消耗减小和电动汽车数量之间的关系。图f主要是给出了峰值能源减小率和出行者出行时间之间的关系，当d取4（1h）时，最消极的人群将增加20min的出行时间，而且这部分人群数量是极少的，因此对出行者出行时间的影响是很小的，几乎可以忽略不计，对于部分出行者，甚至能减少他们的出行时间。最后作者分析了优化策略能带来的金钱的收入，图g给出了不通的d的情况下的金钱节约情况，虽说对于个体或公司而言，这些钱数量不大，但是这些钱用作beneficial to traveler，即作为奖励津贴将是绰绰有余的，这个奖励其实就是一种行为诱导。

参考文献

Xu, Y., Çolak, S., Kara, E.C. et al. Planning for electric vehicle needs by coupling charging profiles with urban mobility. Nat Energy 3, 484–493 (2018). https://doi.org/10.1038/s41560-018-0136-x