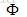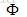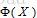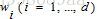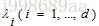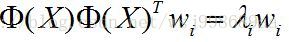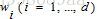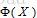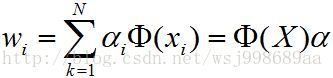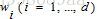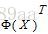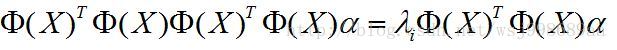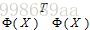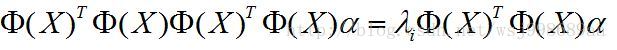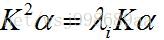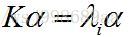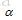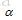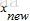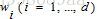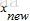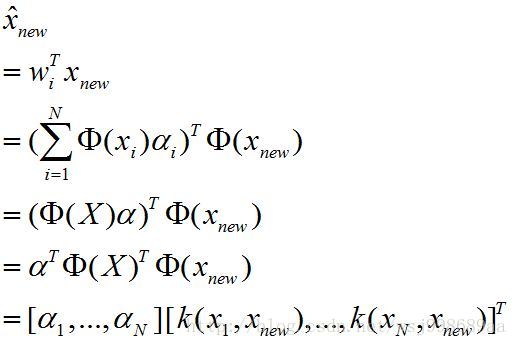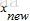解释一下核主成分分析(Kernel Principal Component Analysis, KPCA)的公式推导过程~

本文主要是介绍解释一下核主成分分析(Kernel Principal Component Analysis, KPCA)的公式推导过程~，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

 转载请注明：http://blog.csdn.NET/wsj998689aa/article/details/40398777
 
 KPCA，中文名称”核主成分分析“，是对PCA算法的非线性扩展，言外之意，PCA是线性的，其对于非线性数据往往显得无能为力，例如，不同人之间的人脸图像，肯定存在非线性关系，自己做的基于ORL数据集的实验，PCA能够达到的识别率只有88%，而同样是无监督学习的KPCA算法，能够轻松的达到93%左右的识别率（虽然这二者的主要目的是降维，而不是分类，但也可以用于分类），这其中很大一部分原因是，KPCA能够挖掘到数据集中蕴含的非线性信息。

今天突然心血来潮，想重新推导一下KPCA的公式，期间遇到了几个小问题，上博客查阅，发现目前并没有一个专注于KPCA公式推导的文章，于是决定写一篇这样的博客（转载请注明：http://blog.csdn.NET/wsj998689aa/article/details/40398777）。

1. 理论部分

KPCA的公式推导和PCA十分相似，只是存在两点创新：

1. 为了更好地处理非线性数据，引入非线性映射函数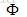，将原空间中的数据映射到高维空间，注意，这个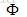是隐性的，我们不知道，也不需要知道它的具体形式是啥。

2. 引入了一个定理：空间中的任一向量（哪怕是基向量），都可以由该空间中的所有样本线性表示，这点对KPCA很重要，我想大概当时那个大牛想出KPCA的时候，这点就是它最大的灵感吧。话说这和”稀疏“的思想比较像。

假设中心化后的样本集合X（d*N，N个样本，维数d维，样本”按列排列“），现将X映射到高维空间，得到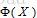，假设在这个高维空间中，本来在原空间中线性不可分的样本现在线性可分了，然后呢？想啥呢！果断上PCA啊！~

于是乎！假设D（D >> d）维向量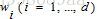为高维空间中的特征向量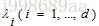，为对应的特征值，高维空间中的PCA如下：

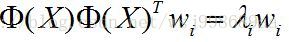（1）

和PCA太像了吧？这个时候，在利用刚才的定理，将特征向量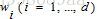利用样本集合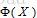线性表示，如下：

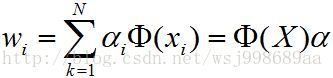（2）

然后，在把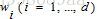代入上上公式，得到如下的形式：

（3）

进一步，等式两边同时左乘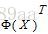，得到如下公式：

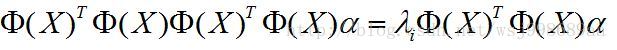（4）

你可能会问，这个有啥用？

这样做的目的是，构造两个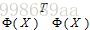出来，进一步用核矩阵K（为对称矩阵）替代，其中：

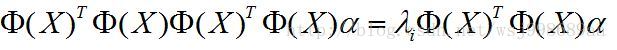（5）

第二个等号，是源于核函数的性质，核函数比较多，有如下几种：

于是，公式进一步变为如下形式：

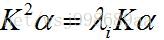（6）

两边同时去除K，得到了PCA相似度极高的求解公式：

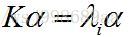（7）

求解公式的含义就是求K最大的几个特征值所对应的特征向量，由于K为对称矩阵，所得的解向量彼此之间肯定是正交的。

但是，请注意，这里的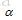只是K的特征向量，但是其不是高维空间中的特征向量，回看公式（2），高维空间中的特征向量w应该是由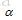进一步求出。

这时有的朋友可能会问，这个时候，如果给定一个测试样本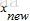，应该如何降维，如何测试？

是这样的，既然我们可以得到高维空间的一组基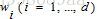，这组基可以构成高维空间的一个子空间，我们的目的就是得到测试样本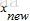在这个子空间中的线性表示，也就是降维之后的向量。具体如下：

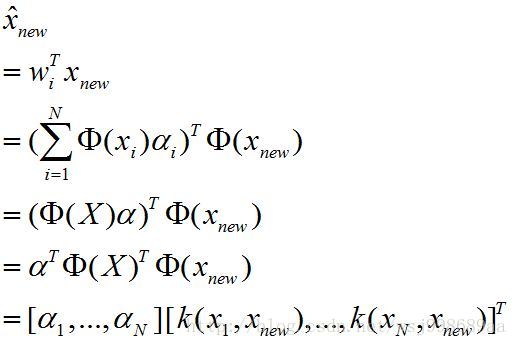（8）

于是呼~就可以对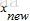降维了，然后就做你想要做的事情。。。。

2. 实验部分

做了一些仿真实验，分别比较了PCA与KPCA之间的效果，KPCA基于不同核函数的效果，二者对于原始数据的要求，以及效果随着参数变化的规律。

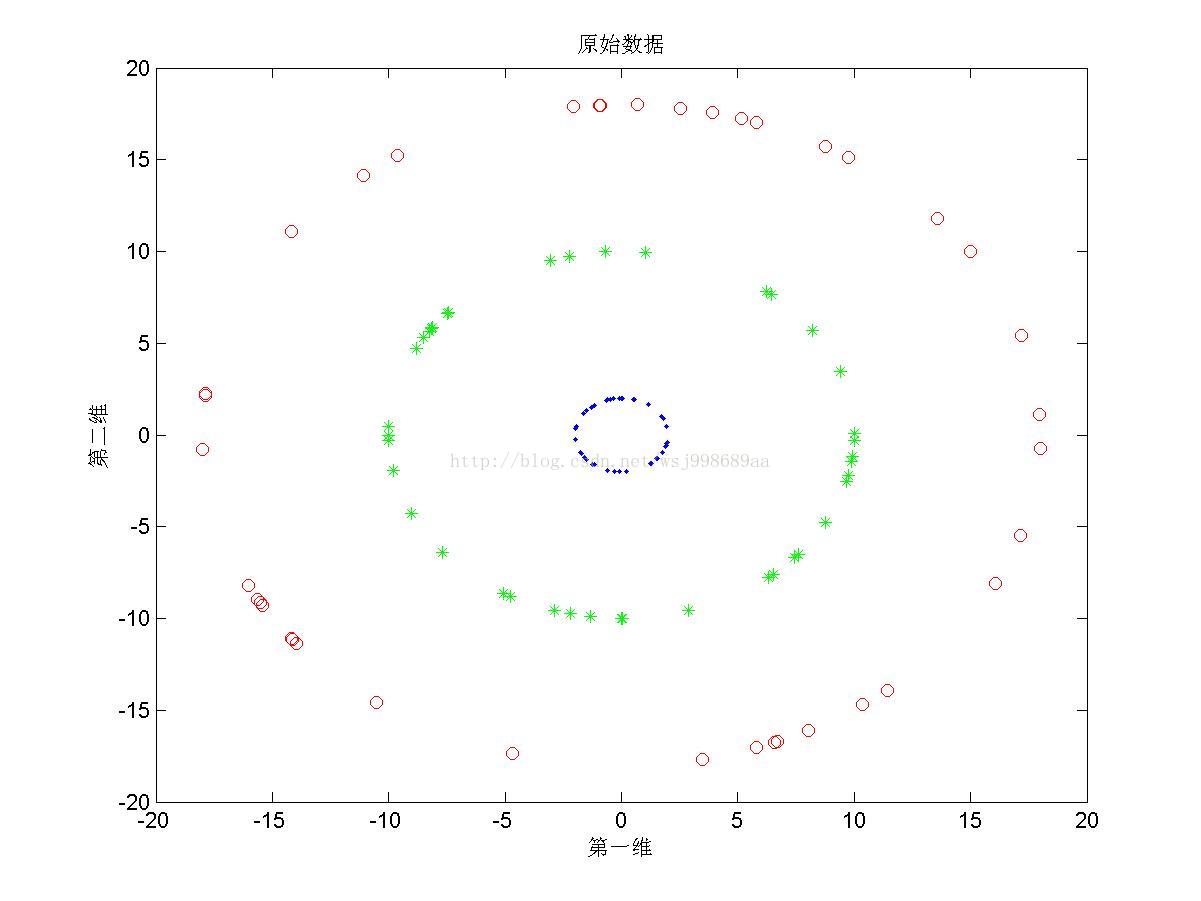
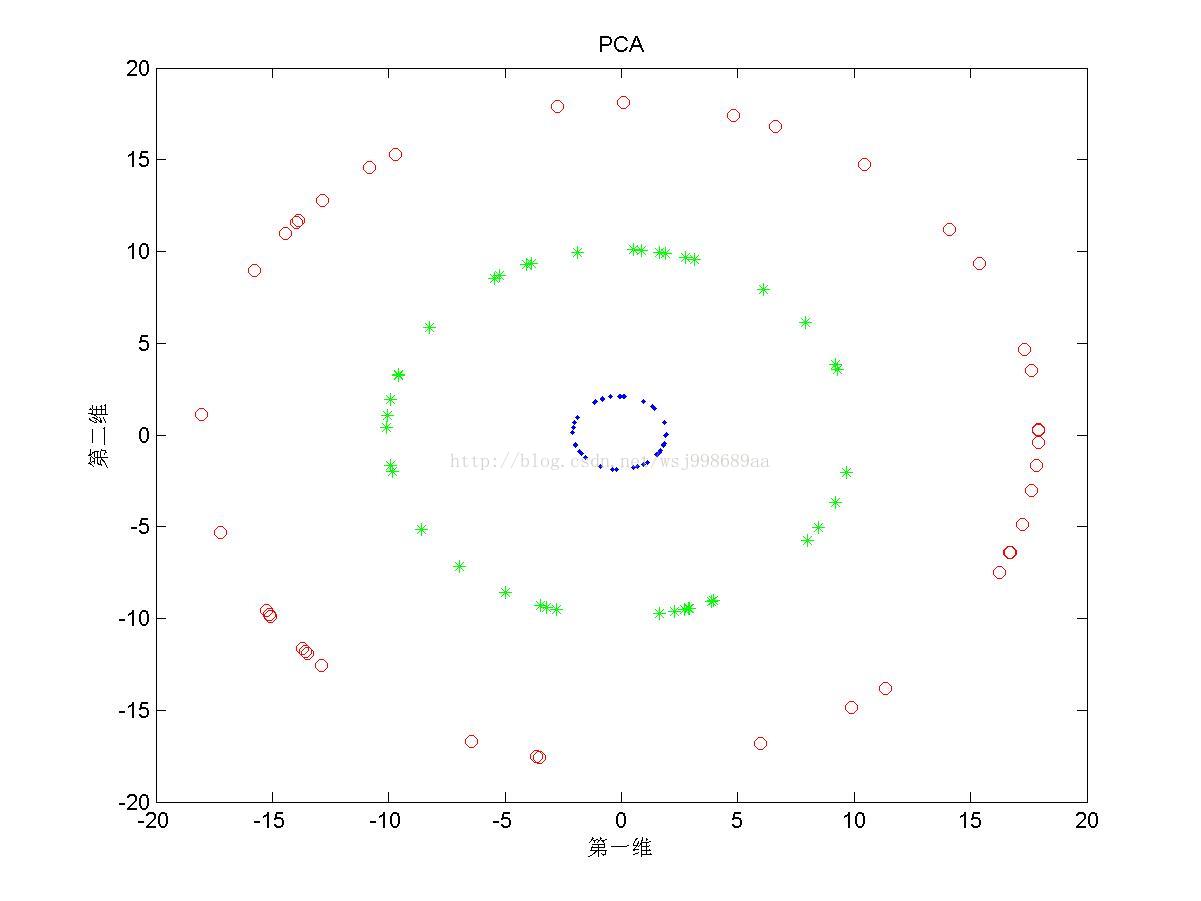
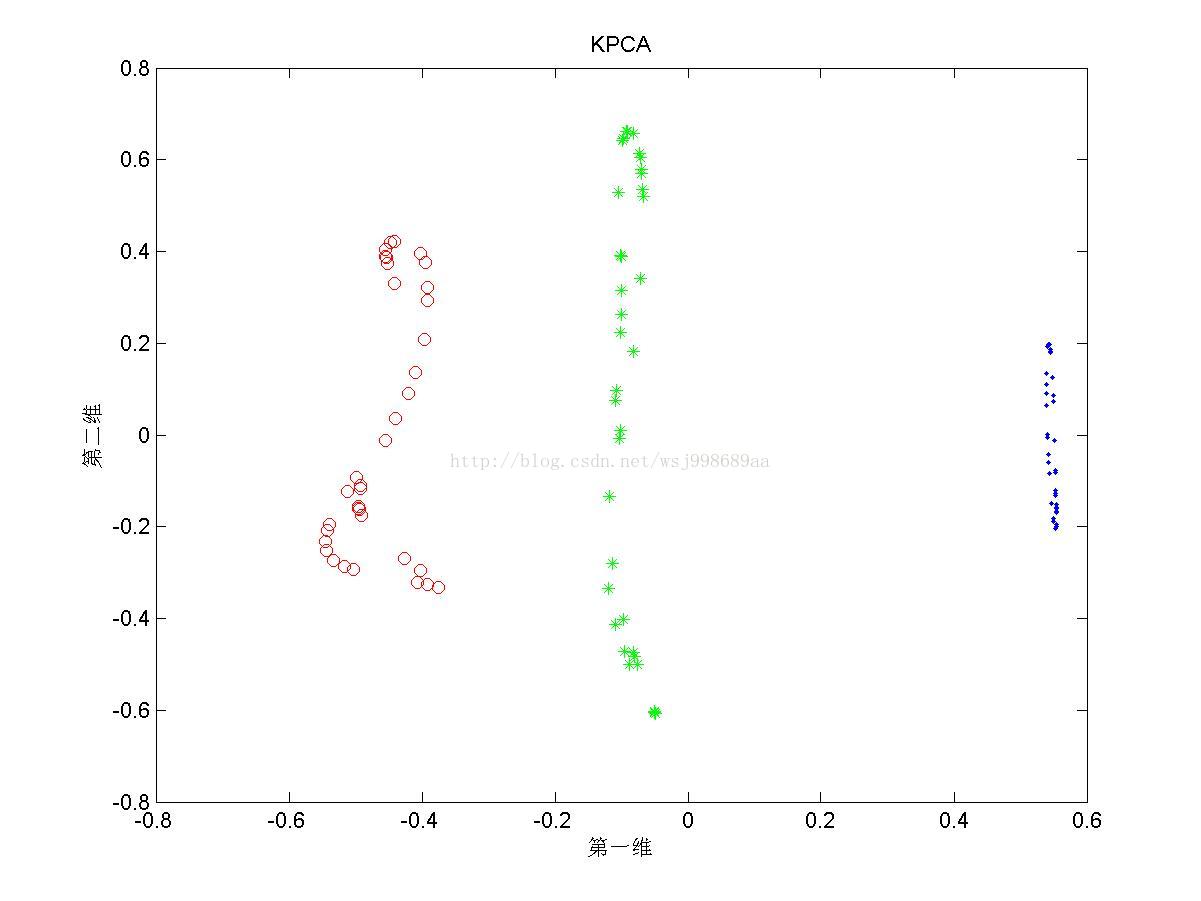
1）下面展示的是“无重叠的”非线性可分数据下，PCA与KPCA（基于高斯核）的区别，注意，原始数据是二维数据，投影之后也是二维数据

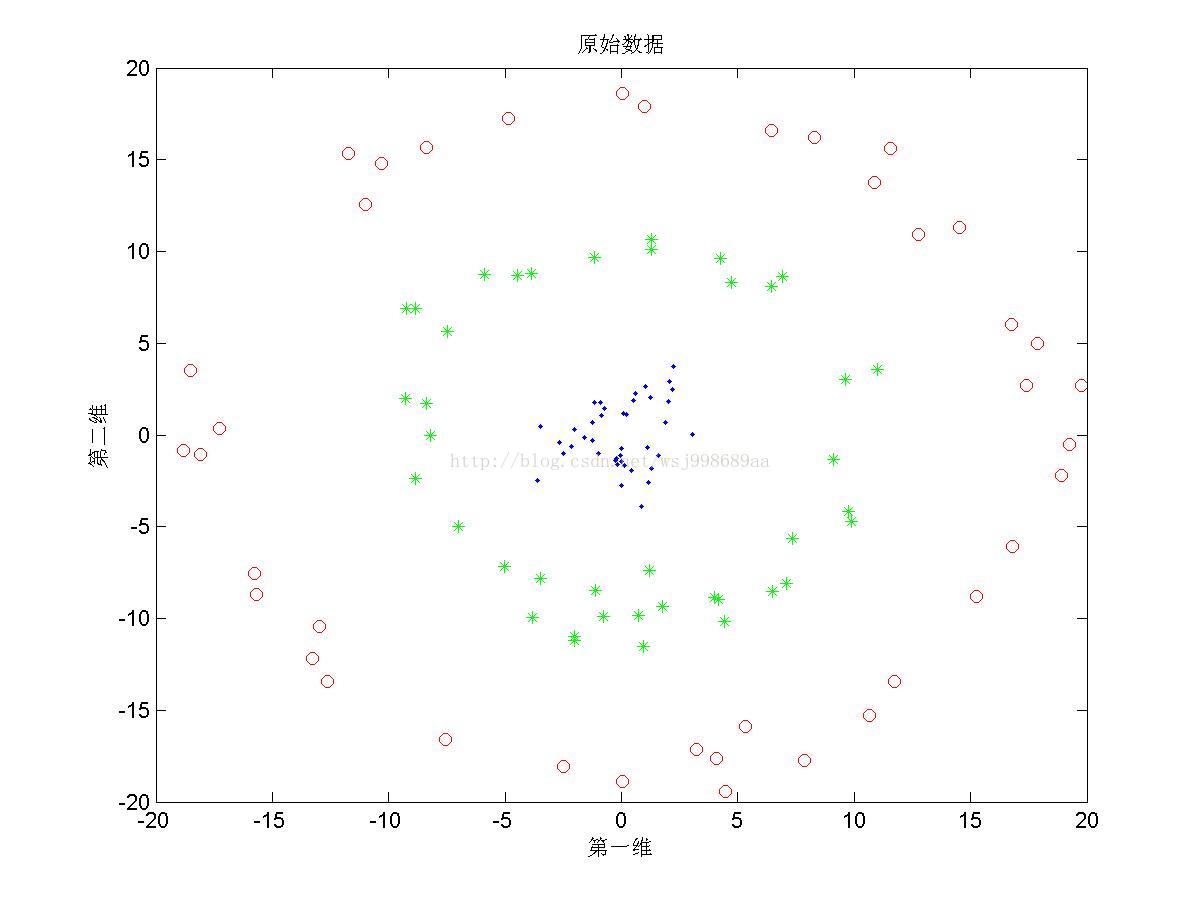
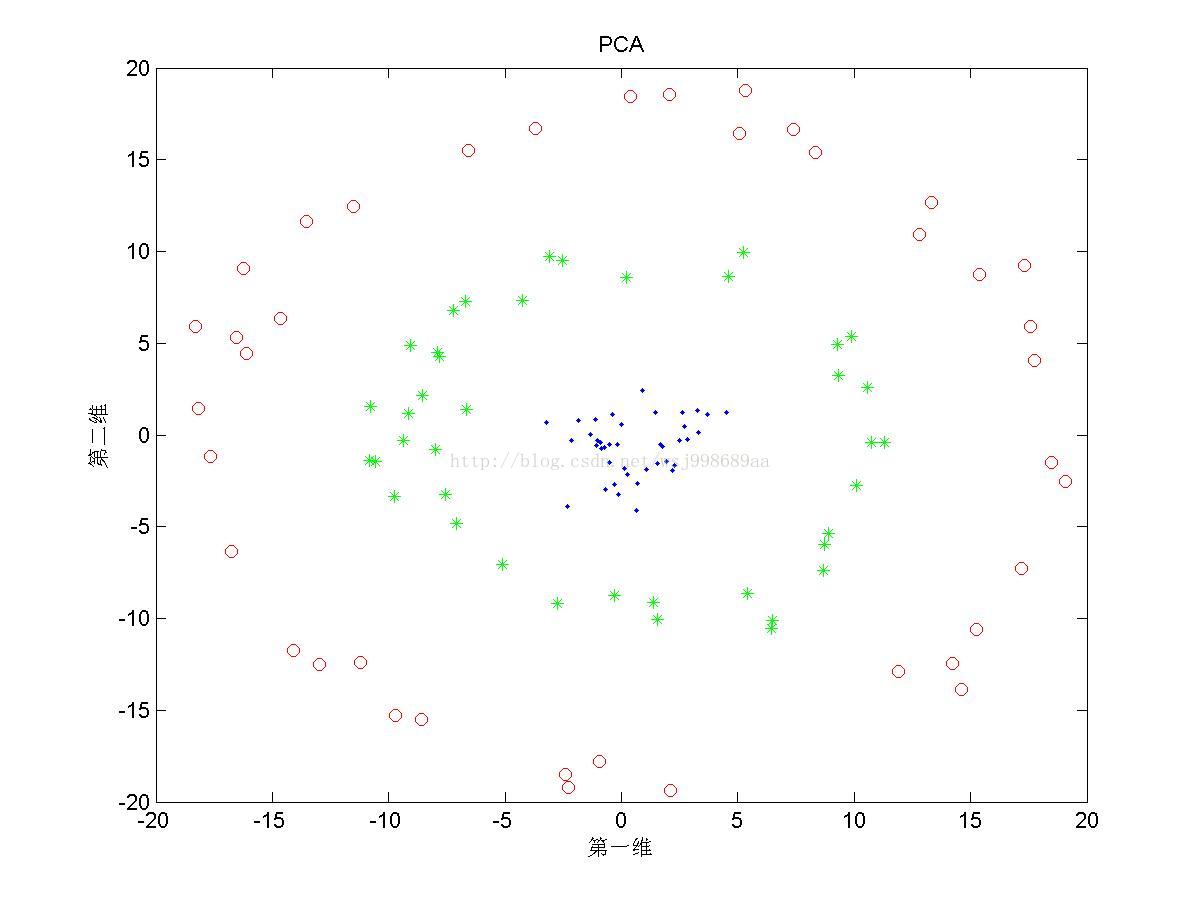
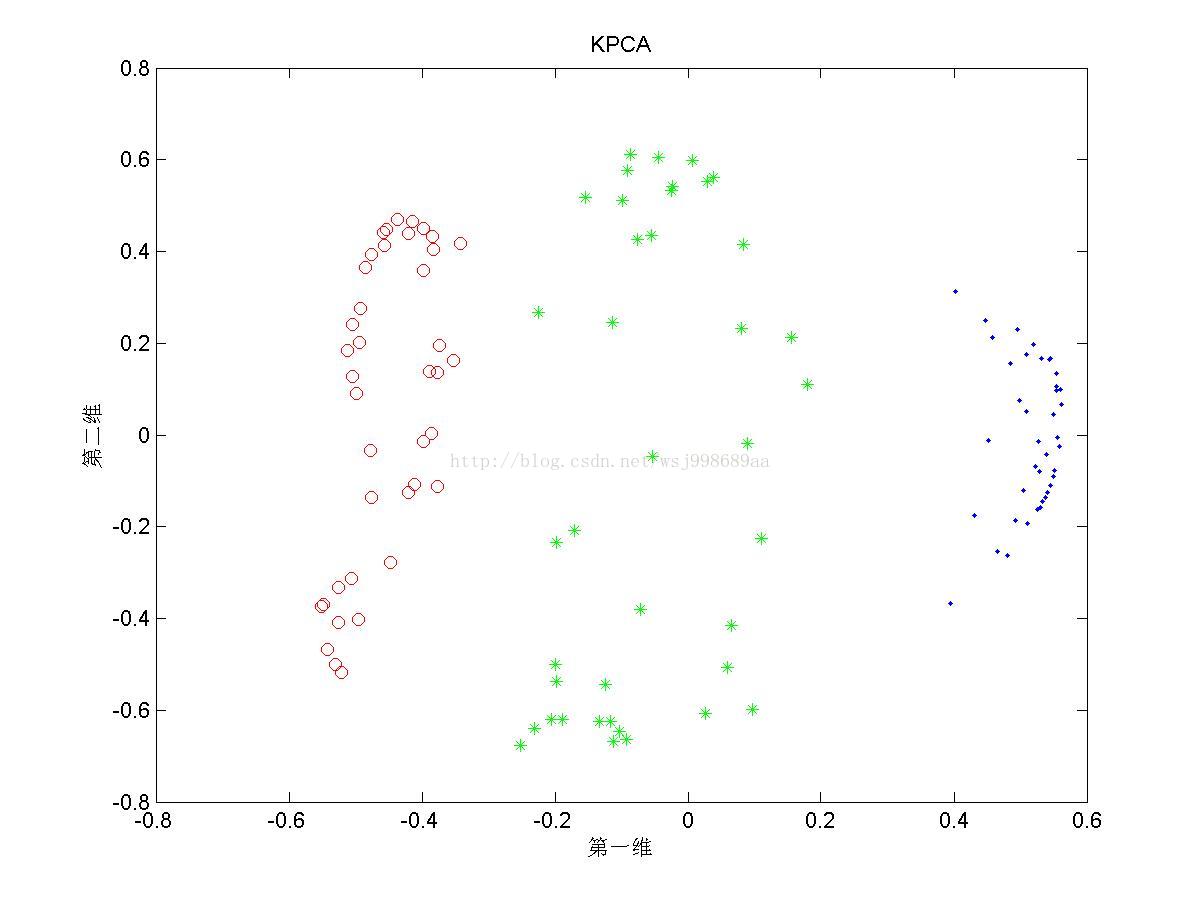
2）下面展示的是“部分重叠的”非线性可分数据下，PCA与KPCA的区别

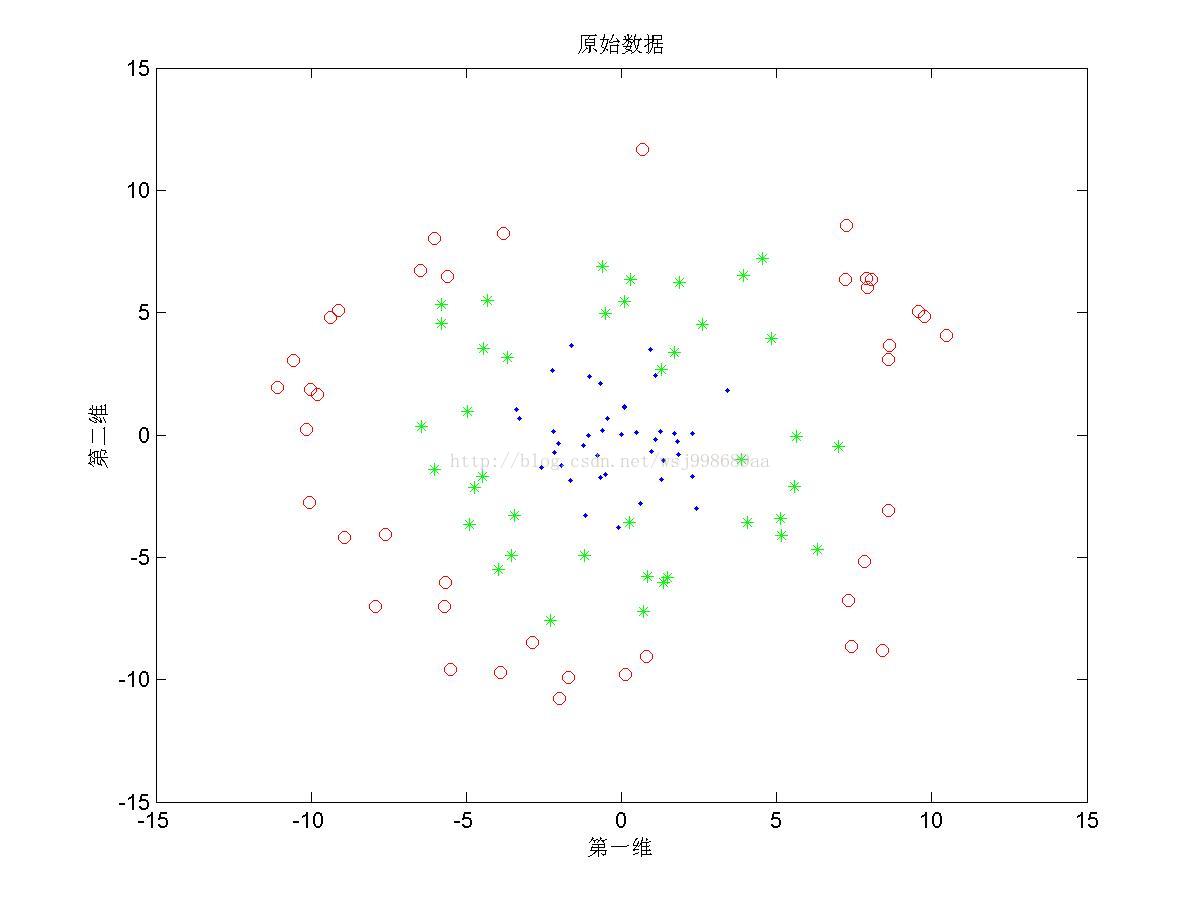
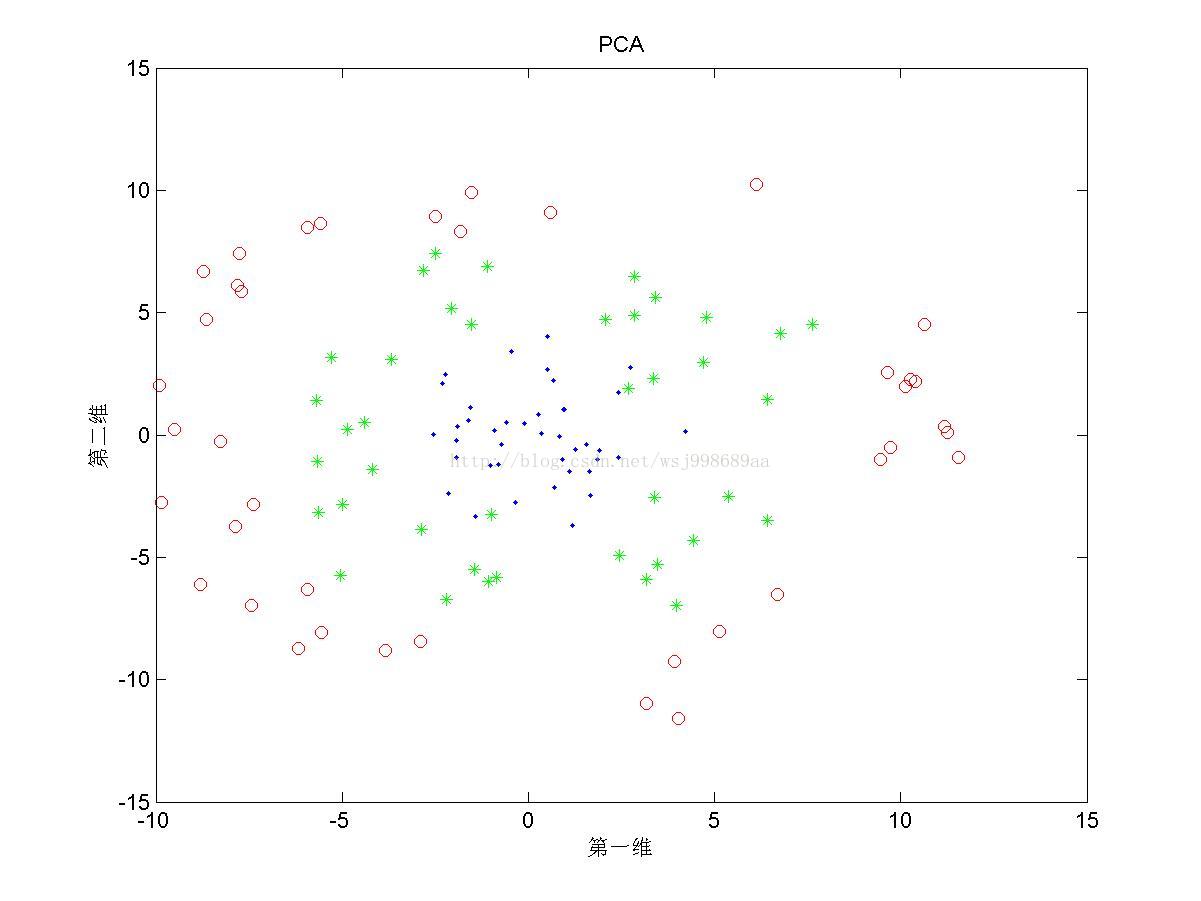
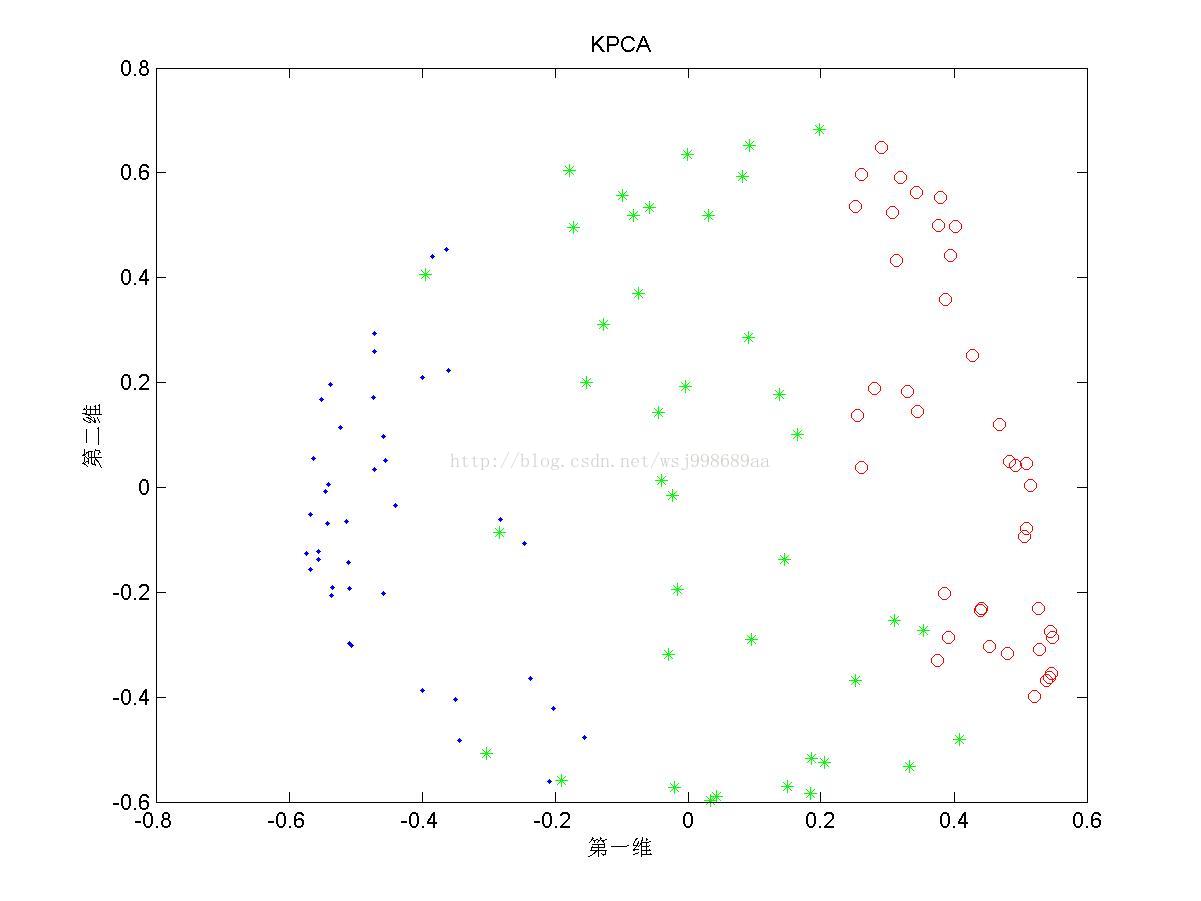
3）下面展示的是“无高斯扰动的”非线性可分数据下，PCA与KPCA的区别

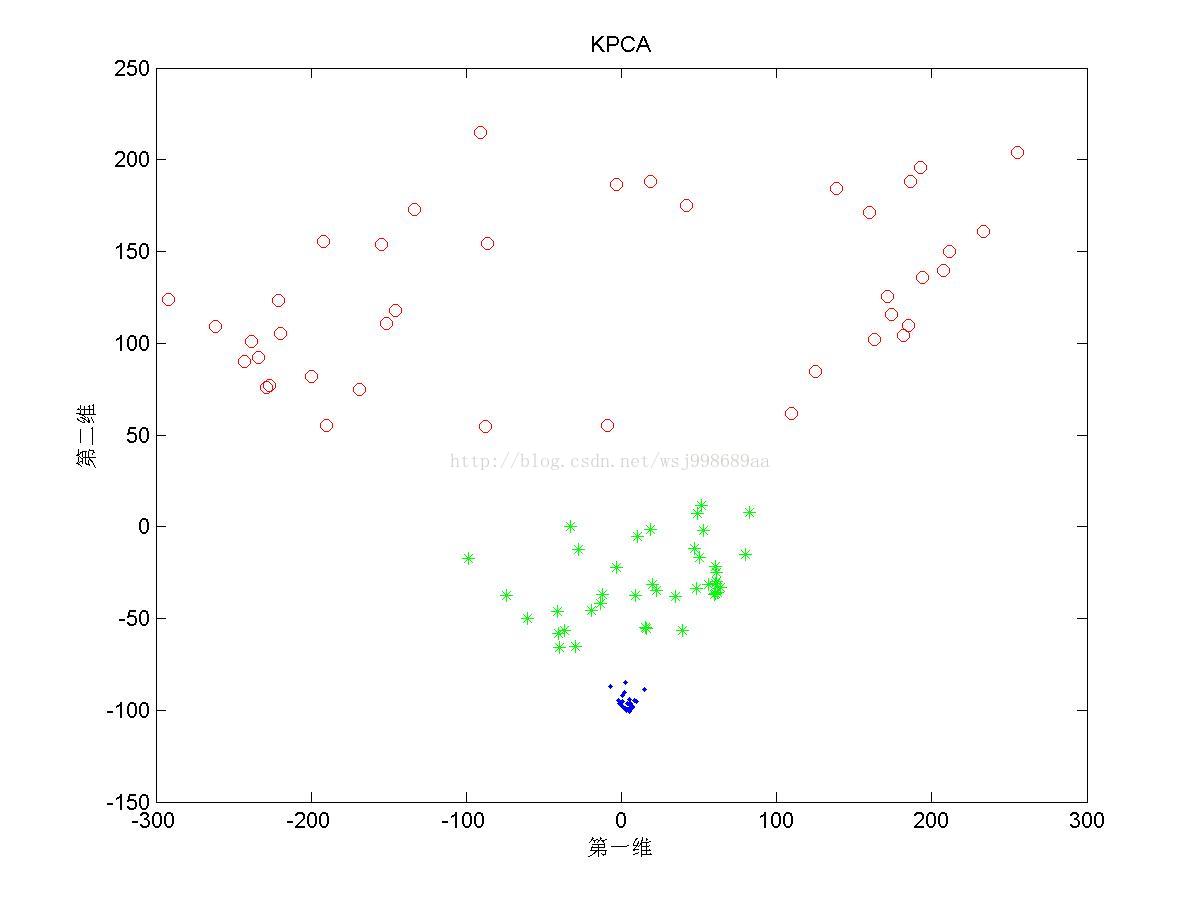
4）下面展示的是上述三类数据下，基于多项式核函数的KPCA效果

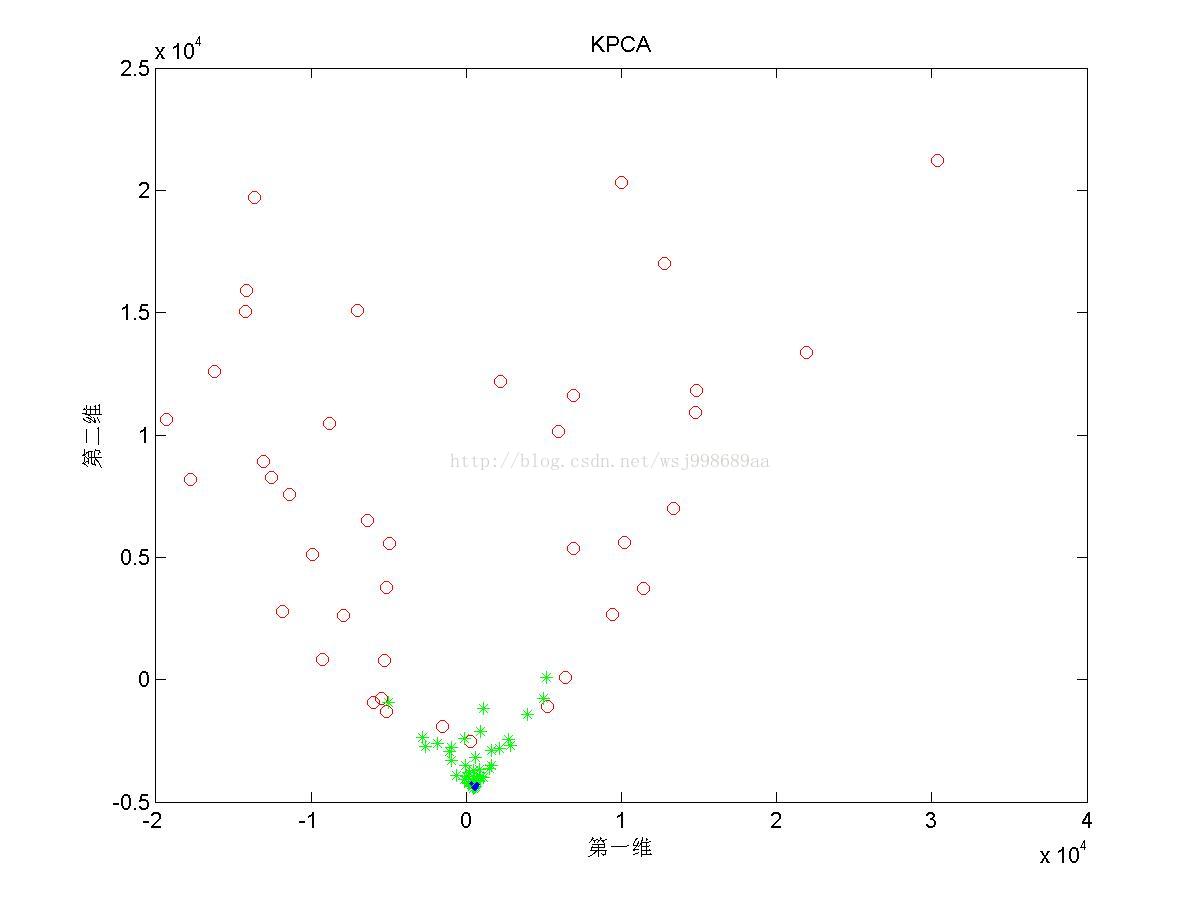
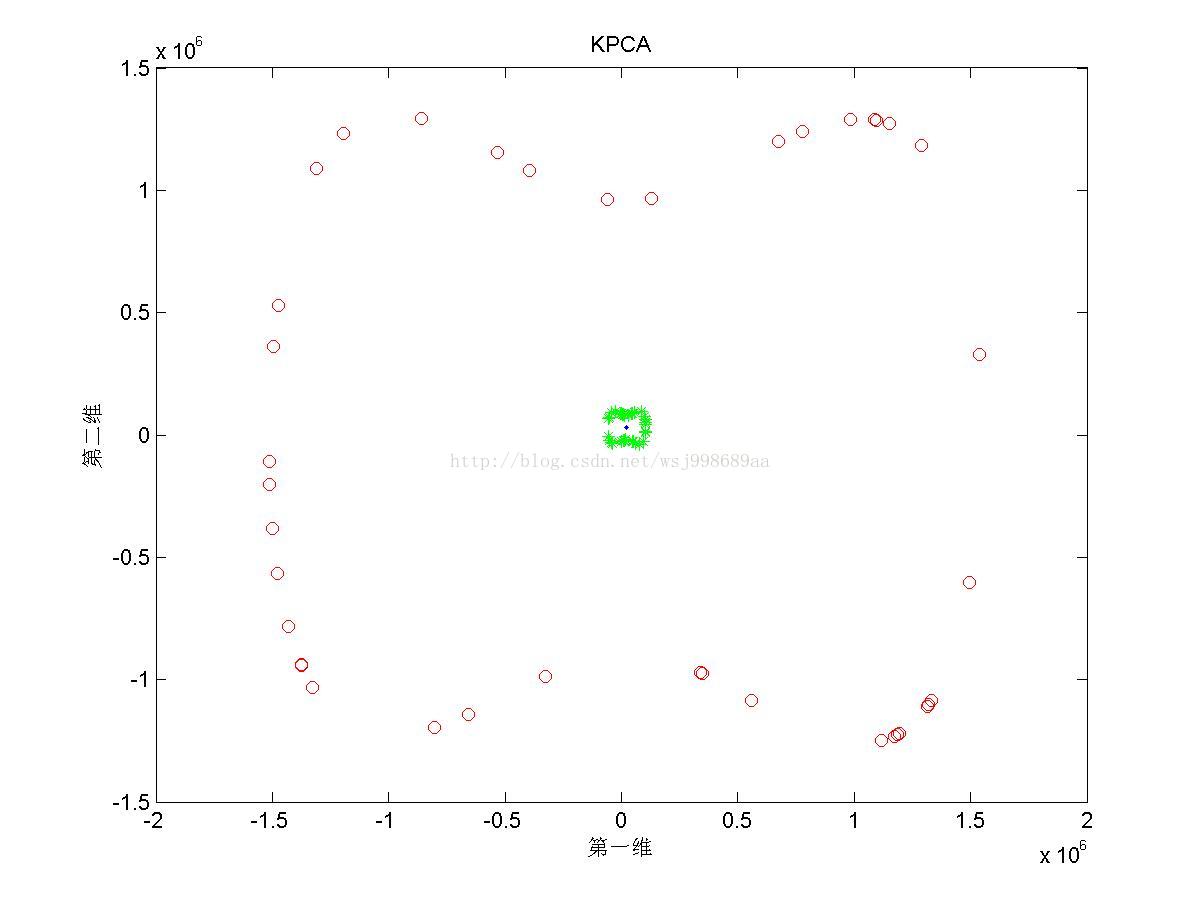
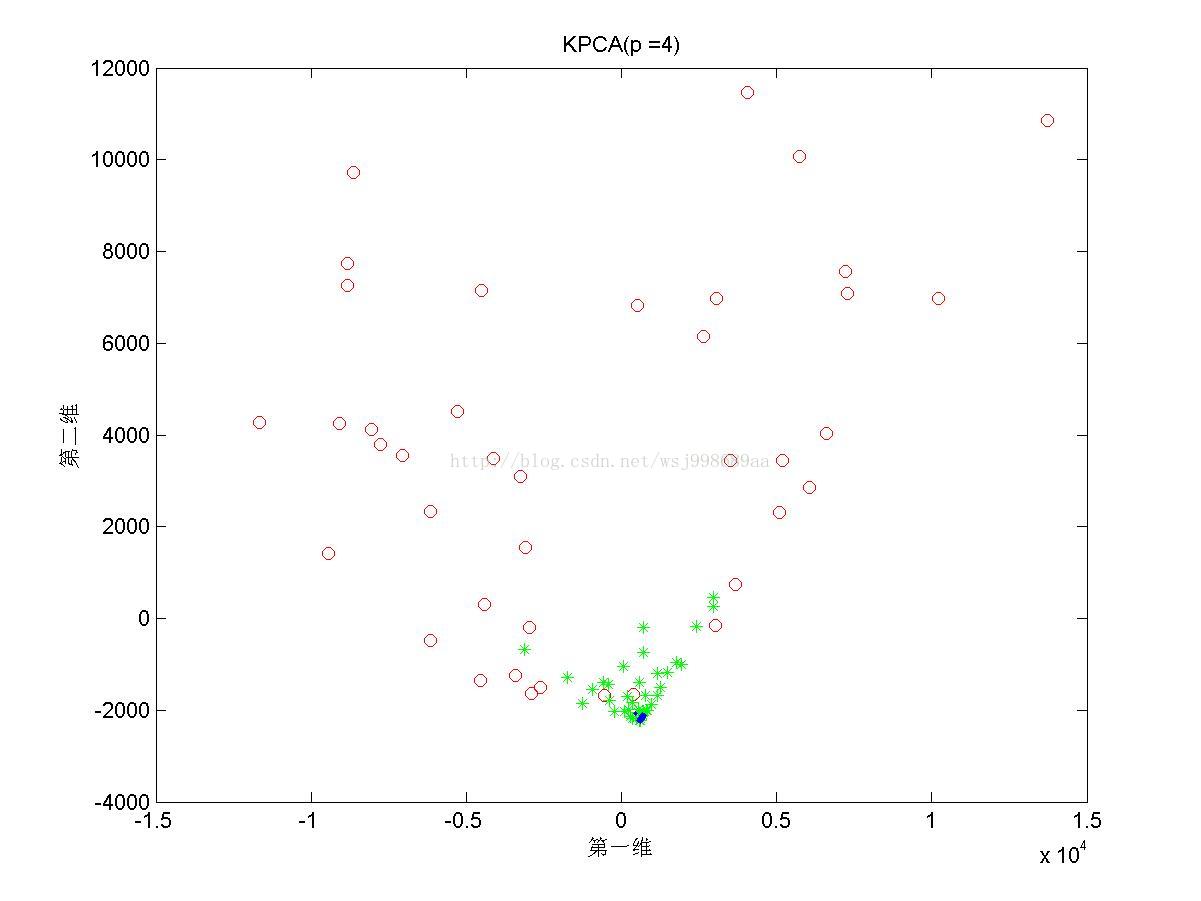
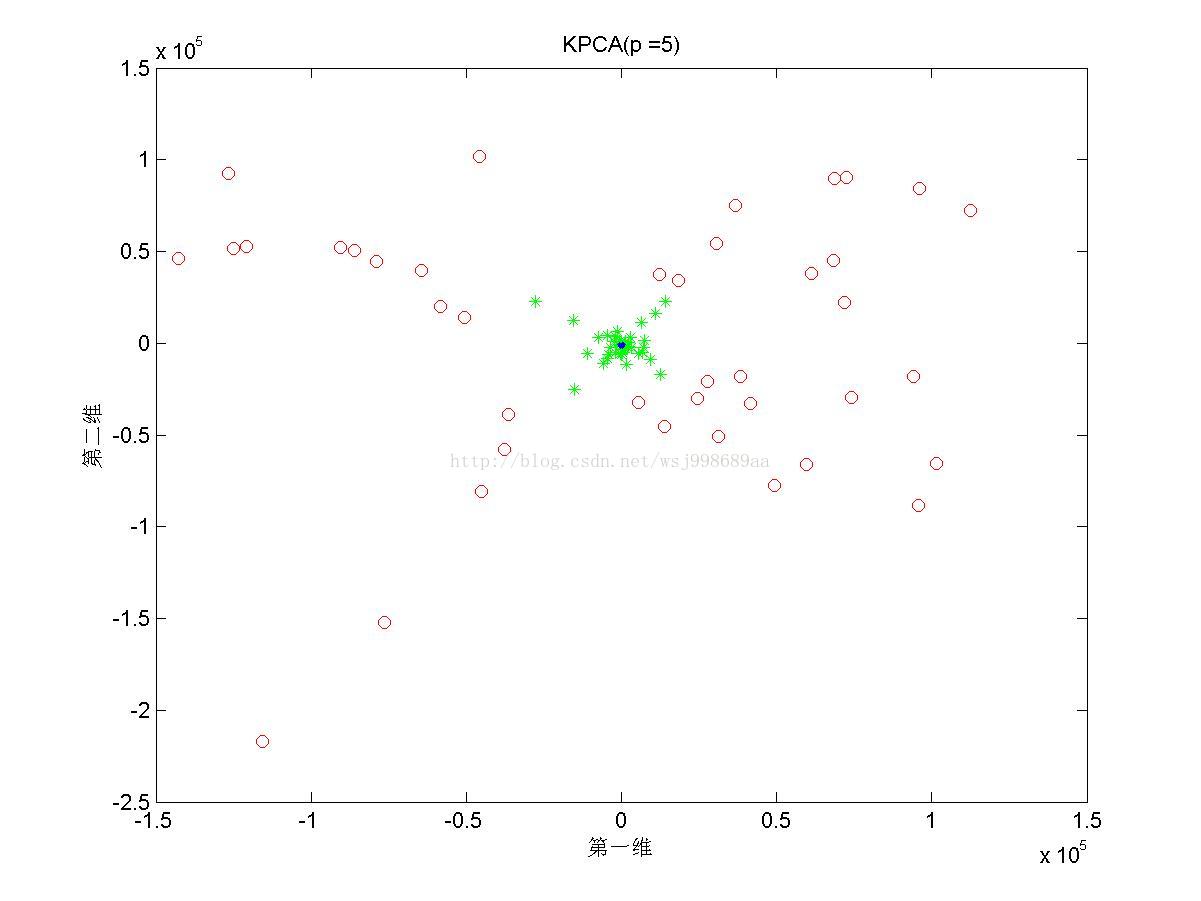
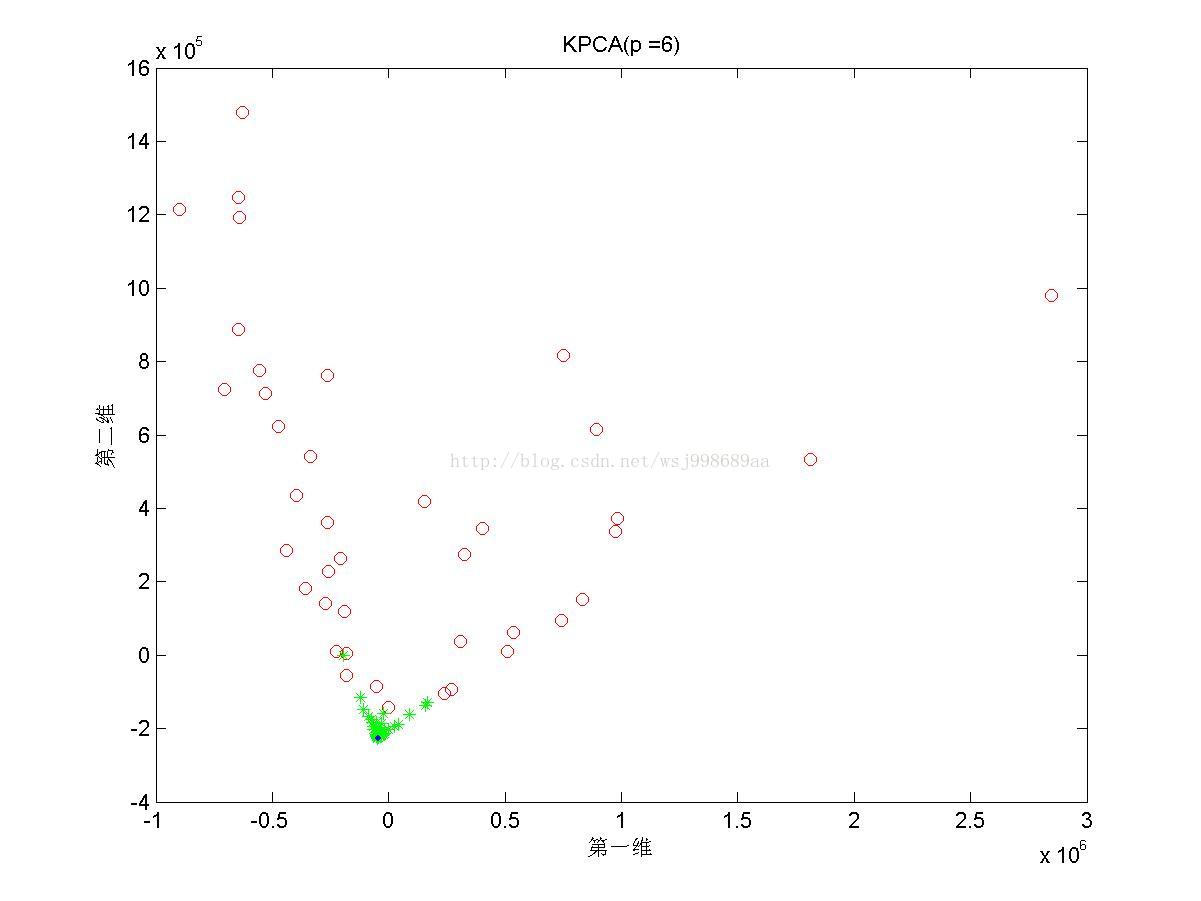
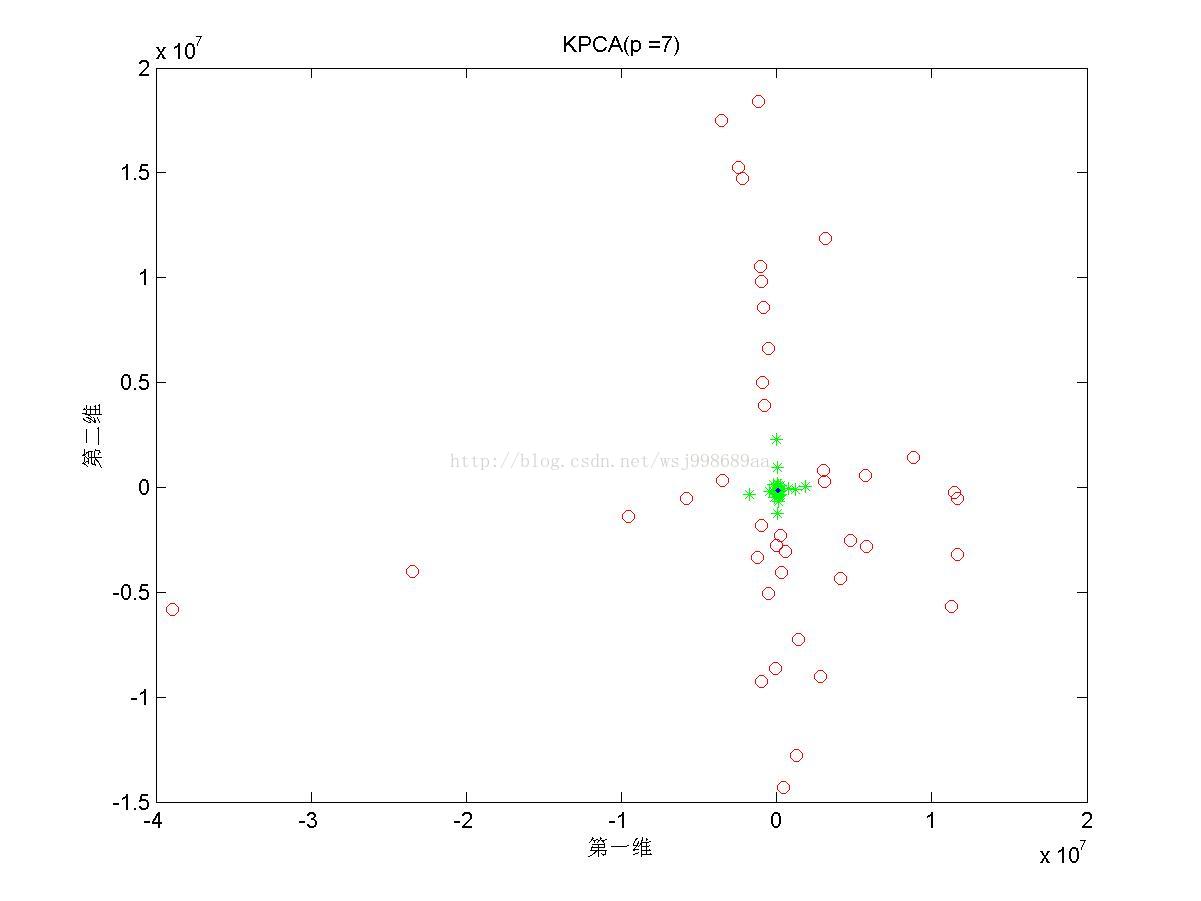
5）下面展示的是在“部分重叠的”非线性可分数据下，基于多项式核函数的KPCA在不同多项式参数下的效果图

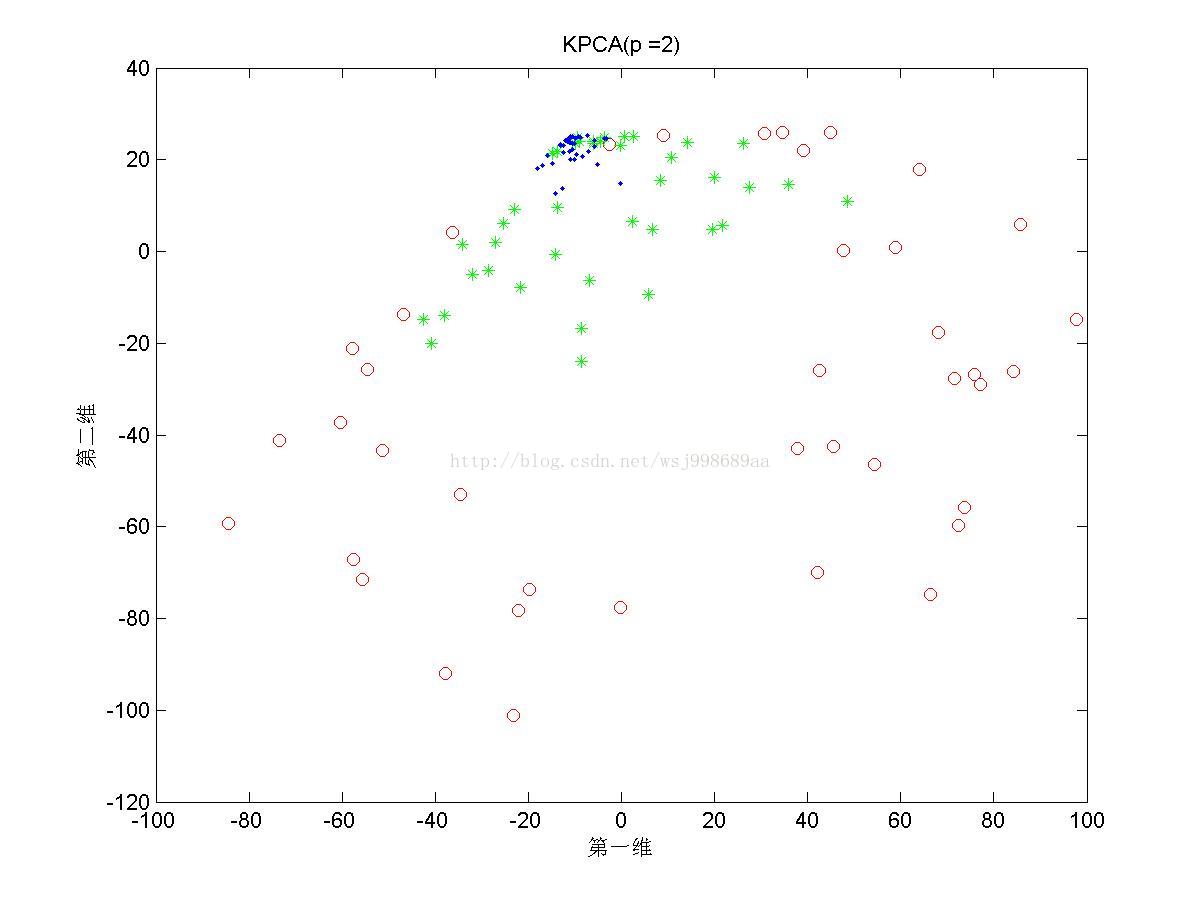
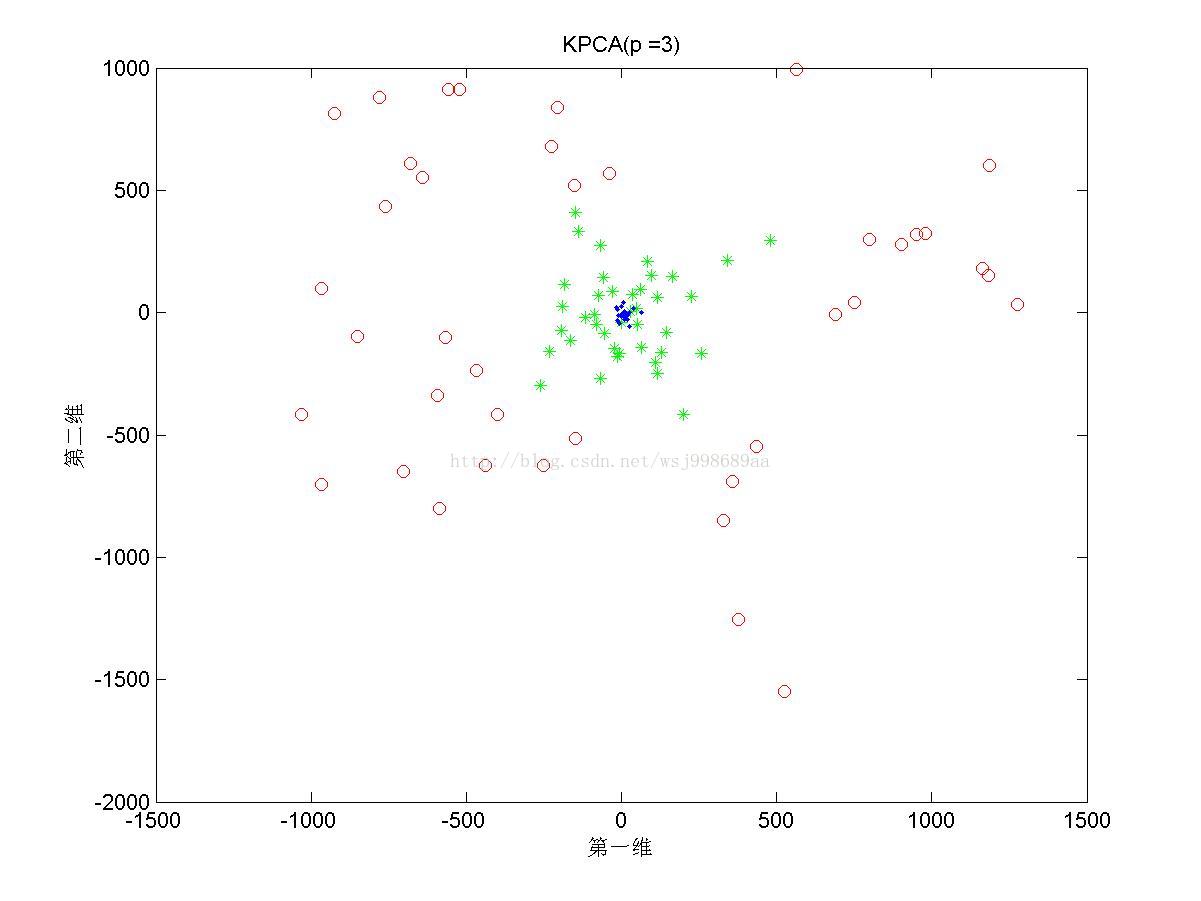
3. 实验结论

1. 从2.1中我们可以看出，PCA与KPCA对于非线性数据各自的处理能力，仔细观察PCA其实只对原始数据进行了旋转操作，这是由于其寻找的是数据的“主要分布方向”。KPCA可以将原始数据投影至线性可分情况，其原因就是第一部分所说的内容。

2. 至于为何将数据分为“无重叠”，“部分重叠”，“无高斯扰动”，是自己在试验中发现，对于部分重叠的数据，KPCA不能将数据投影至完全线性可分的程度（2.3第三幅图中，不同类别数据仍旧存在重叠现象），这说明KPCA只是个无监督的降维算法，它不管样本的类别属性，只是降维而已。

3. 这里提供了高斯核与多项式核的效果，我们很容易发现，二者的效果有很大不同，这直观地说明不同核函数具有不同的特质。并且，针对于无高斯扰动数据，始终没有找到参数p，有可能针对这类数据，多项式核函数无能为力。

4. 2.5中展示了多项式核的参数影响，我们可以发现，往往p值是偶数时，数据可以做到近似线性可分，p是奇数时，数据分布的形态也属于另外一种固定模式，但是不再是线性可分。

4. 代码

前面给出了自己对KPCA的理论解释，以及做的一些基础实验，不给出实现代码，就不厚道了，代码如下所示，一部分是KPCA算法代码，另一部分是实验代码。

[plain]  view plain copy  
 function [eigenvalue, eigenvectors, project_invectors] = kpca(x, sigma, cls, target_dim)  
     % kpca进行数据提取的函数  
     psize=size(x);  
     m=psize(1);     % 样本数  
     n=psize(2);     % 样本维数  
   
   
     % 计算核矩阵k  
     l=ones(m,m);  
     for i=1:m  
         for j=1:m  
            k(i,j)=kernel(x(i,:),x(j,:),cls,sigma);   
         end  
     end  
   
   
     % 计算中心化后的核矩阵  
     kl=k-l*k/m-k*l/m+l*k*l/(m*m);    
   
   
     % 计算特征值与特征向量  
     [v,e] = eig(kl);   
     e = diag(e);  
   
   
     % 筛选特征值与特征向量  
     [dump, index] = sort(e, 'descend');  
     e = e(index);  
     v = v(:, index);  
     rank = 0;  
     for i = 1 : size(v, 2)  
         if e(i) < 1e-6  
             break;  
         else  
             v(:, i) = v(:, i) ./ sqrt(e(i));  
         end  
         rank = rank + 1;  
     end  
     eigenvectors = v(:, 1 : target_dim);  
     eigenvalue = e(1 : target_dim);  
   
   
     % 投影  
     project_invectors = kl*eigenvectors;   %计算在特征空间向量上的投影   
 end  

[plain]  view plain copy  
 function compare  
     clear all;  
     close all;  
     clc;  
       
     % 生成非线性可分的三类数据  
     if exist('X1.mat')  
         load 'X1.mat'  
         load 'X2.mat'  
         load 'X3.mat'  
         figure(1)         
         plot(X1(1, :),X1(2, :) ,'ro')  
         hold on;  
         plot(X2(1, :),X2(2, :),'g*')  
         hold on;  
         plot(X3(1, :),X3(2, :),'b.')  
         hold on;  
           
         title('原始数据');  
         xlabel('第一维');  
         ylabel('第二维');  
         saveas(gcf, '原始数据图.jpg')  
     else  
         [X1, X2, X3] = generate_data();  
         save 'X1.mat'  X1  
         save 'X2.mat'  X2  
         save 'X3.mat'  X3  
     end  
   
     X = [X1 X2 X3];  
     [nFea, nSmps] = size(X);  
     nClsSmps = nSmps / 3;  
       
     % PCA  
     [vec_pca, Y_pca, value_pca] = princomp(X');  
     Y_pca = Y_pca';  
       
     figure(2);  
     plot(Y_pca(1, 1 : nClsSmps),Y_pca(2, 1 : nClsSmps), 'ro');  
     hold on;  
     plot(Y_pca(1, nClsSmps + 1 : 2 * nClsSmps),Y_pca(2, nClsSmps + 1 : 2 * nClsSmps), 'g*');  
     hold on;  
     plot(Y_pca(1, 2 * nClsSmps + 1 : end),Y_pca(2, 2 * nClsSmps + 1 : end), 'b.');  
     hold on;  
     title('PCA');  
     xlabel('第一维');  
     ylabel('第二维');  
     saveas(gcf, 'PCA投影图.jpg')  
       
     % KPCA  
     percent = 1;  
     var   = 2; % 1 代表高斯核，2代表多项式核，3代表线性核  
     sigma = 6; % 核参数  
     [vec_KPCA, value_KPCA, Y_pca] = kpca(X', sigma, var, 2);  
     Y_pca = Y_pca';  
       
     figure(3);  
     plot(Y_pca(1, 1 : nClsSmps),Y_pca(2, 1 : nClsSmps), 'ro');  
     hold on;  
     plot(Y_pca(1, nClsSmps + 1 : 2 * nClsSmps),Y_pca(2, nClsSmps + 1 : 2 * nClsSmps), 'g*');  
     hold on;  
     plot(Y_pca(1, 2 * nClsSmps + 1 : end),Y_pca(2, 2 * nClsSmps + 1 : end), 'b.');  
     hold on;  
     str = strcat('KPCA', '(p =', num2str(sigma), ')');  
     title(str);  
     xlabel('第一维');  
     ylabel('第二维');  
     str = strcat(str, '.jpg')  
     saveas(gcf, str)  
 end  