本文主要是介绍PRN(20210425):Gradient based sample selection for online continual learning,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
智能体需要具备不断适应环境的能力,这就使得其必须能够利用当前与环境或其他智能体交互的样本进行在线、增量式学习的能力。深度神经网络被广泛用于作为学习的模型,应用于这样的增量式学习任务时存在灾难性遗忘问题。缓解该问题的一种方法是:利用一个类似于DQN的经验回放单元存储重要的历史样本用来回忆(rehearsal)历史知识,使模型克服(目前还做不到“克服”,个人觉得用“缓解”更合适)灾难性遗忘问题。该方法的核心要点是如何从持续到来的数据中选择合适的样本。对于一个样本可持续的学习任务,数据一般都是在线产生的,无法保证现有大部分研究所假定的独立同分布条件。
https://github.com/rahafaljundi/Gradient-based-Sample-Selection
一、持续学习:一种带约束的优化问题
1.1 问题阐述
目标:基于当前样本优化损失函数,并同时不增加历史已学习样本的损失值。
根据以上目标可得如下带约束的优化问题:
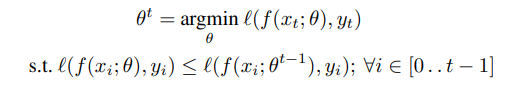
其中, ( x t , y t ) (x_t, y_t) (xt,yt)为当前时刻获得的样本, f ( . ; θ ) f(.;\theta) f(.;θ)表示参数为 θ \theta θ的模型, l l l为损失函数, t t t为当前样本的索引, i i i表示历史样本的索引。
问题的约束可以进一步变换成梯度空间的约束:
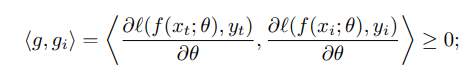
随着学习的进行,历史样本数越来越多,计算这样一个约束的时间成本也越来越大,外加存储历史样本的空间成本。实际情况允许的是,保留一部分更加有用的历史样本,例如采用一个固定大小为M的记忆单元 M \mathcal{M} M.
1.2 Sample Selection as Constraint Reduction
我们通过选择M个样本,使得由它们表示的约束与原始的约束问题接近:
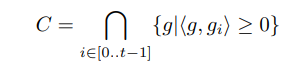
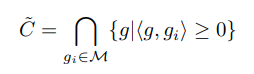
C C C和 C ^ \hat{C} C^的示意图如下:
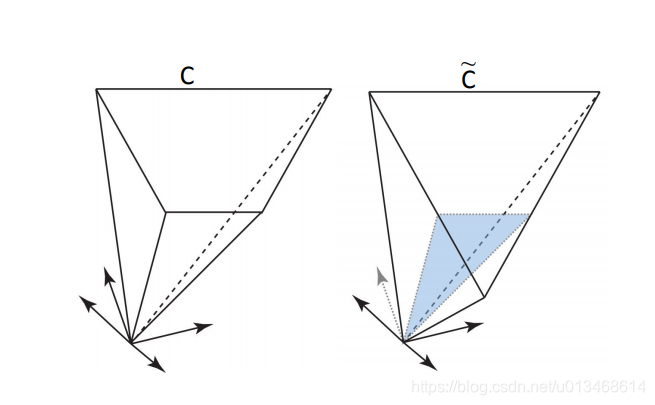
于是可得以下优化问题:
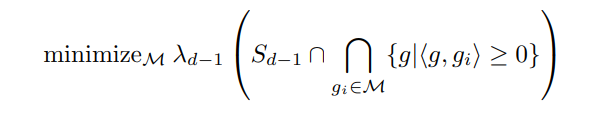
1.3 一个可行区域最小化的经验替代形式
前面给出的形式很难在数学上求解,因此用以下的形式替代:
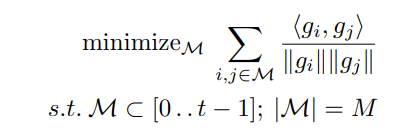
可以这样理解:优化目的是为了减小可行集,必须充分增加replay memory中各对样本的梯度夹角。
通过以以推导发现,上面优化可以转换成最大化梯度方向的方差:
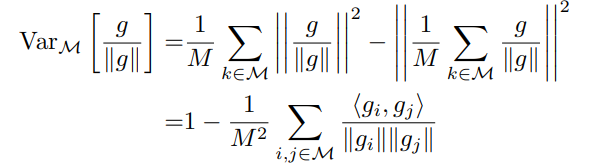
note: 重要样本选择问题最后转变成最大化固定size replay memory中样本的损失梯度方向的方差。replay memory中的梯度方向的方差的最大化,等于把一个社区里不同的意见代表给找了出来,如果一个方案能够满足由这样的不同意见代表组成的监察组,那么说明这样的方案兼顾了所有。对应到本文的问题,那就是即照顾到了现有样本的学习,又保持历史知识的不遗忘。除了可以用损失梯度方向的方差最大化这一信息来选择样本,replay memory还可以直接根据样本的方法或样本在网络隐含层输出的特征方差来选择重要样本。
1.4 在线样本选择
1.4.1 整数二次规划
可以等价成如下形式:
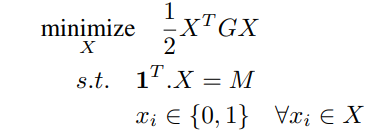
其中, G = < g i , g j > ∣ ∣ g i ∣ ∣ ∣ ∣ g j ∣ ∣ G=\frac{<g_i, g_j>}{||g_i||||g_j||} G=∣∣gi∣∣∣∣gj∣∣<gi,gj>, x x x非1即0,表示某一样本是否被中。用白话说,就是从N个样本中,选择M个样本,并且它们的损失梯度方向夹角余弦值和最小。

1.4.2 In-exact贪婪替换
当需要维护的replay memory很大时,基于整数规划的方法计算量很大。因此,提出贪婪替换的方法。
贪婪替换也能够实现replay memory中样本多样性的目的,并且成本比整数二次规划要小很多。贪婪替换的核心思想是:给每一个replay memory中的样本维护一个评分,这个评分是通过计算该样本与从replay memory中随机选择出的固定数量样本的最大余弦相似量获得的。在最开始时,replay memory未填满,我们直接将新来的样本附加评分加入replay memory。一旦replay memory达到最大容量,我们随机的从replay memory中选择样本作为被替换的对象。随机的概率由标准后的评分获得。然后,比较新样本的与候选替换对象的评分来决定替换是否进行。

其中, P ( i ) = C i / ∑ j C j P(i)=C_i/\sum_j C_j P(i)=Ci/∑jCj为replay memory中被选中用于替换新样本的候选样本; C i / ( c + C i ) C_i/(c+C_i) Ci/(c+Ci)为候选样本被新样本替换的概率, C i C_i Ci为候选样本的分数, c c c为新样本的分数。
End
by WindSeS 2021-4-25
这篇关于PRN(20210425):Gradient based sample selection for online continual learning的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








