相机内参标定和畸变校正以及张氏标定法

一些坐标系

       世界坐标系：是一个假想的坐标系，用作一般参考，可根据需要自由定义。
       在我们的双目相对位姿测量系统中，世界坐标系一般定义与左相机的摄像机坐标系重合，这样的话左相机的R为单位矩阵，T为零向量。双目视觉中一般将世界坐标系原点定在左相机或者右相机或者二者X轴方向的中点。

相机标定

       对于N张无畸变的图像来说，共有4个内参+6N个外参来标定，每张棋盘图上有4个有效的角点，可以提供8个约束，则需要8N>=4+6N8N>=4+6N8N>=4+6N，则至少需要2张无畸变的图像可以求出相机的内参和外参，实际上一般可以取10张，从而利用最小二乘得到更精确的解。在求出了内参和外参后，即可根据剩余的点坐标求出畸变相关参数。
图像坐标和像素坐标
       主要是定义的原点不同，图像坐标u，v原点在图像中心即光心，像素坐标x，y 原点一般在左上角；图像坐标系的单位是mm，属于物理单位，而像素坐标系的单位是pixel。
相机标定参数例子
       200万pixels工业摄像机为例：已知摄像头的焦距为4mm,像片的尺寸大小为640x480，传感器尺寸为5856 μm x 3276 μm，像素大小为3μm x 3μm。由上面已知条件可求得内参矩阵 $fx，fy$为焦距，一般情况下，二者相等，u0、v0为主点坐标（相对于成像平面），beta为坐标轴倾斜参数，理想情况下为0。

       将内参矩阵分解为切变(shear,类似于将长方形压成平行四边形的变形方式)、缩放，平移变换，分别对应轴倾斜、焦距、主点偏移， 右边三个矩阵依次是：2D平移、2D缩放、2D切变。缩放和切变可改变顺序

透镜畸变及校正模型

径向畸变

       最常见的畸变，沿着成像镜头半径方向凹凸的坍缩和膨胀，即枕形或桶形。产生原因是光线在原理透镜中心的地方比靠近中心的地方更加弯曲。

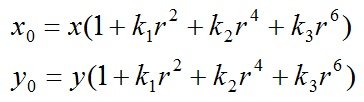
       成像仪光轴中心的畸变为0，沿着镜头半径方向向边缘移动，畸变越来越严重。畸变的数学模型可以用主点（principle point）周围的泰勒级数展开式的前几项进行描述，通常使用前两项，即k1和k2，对于畸变很大的镜头，如鱼眼镜头，可以增加使用第三项k3来进行描述，成像仪上某点根据其在径向方向上的分布位置，调节公式为：

切向畸变
       切向畸变是由于透镜本身与相机传感器平面（成像平面）或图像平面不平行而产生的，这种情况多是由于透镜被粘贴到镜头模组上的安装偏差导致。

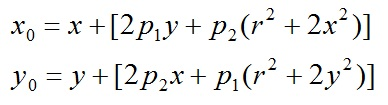
       综上，我们一共需要5个畸变参数（k1、k2、k3、p1和p2 ）来描述透镜畸变。

张氏标定法

       只关注了影响最大的径向畸变（k1，k2），并忽略3阶以上的畸变量。（阶数，即求导次数，不同于数的几次幂数）

注意事项

• Corners中的角点坐标顺序排列规律不一定是以行从左上到右下。
• 如果一部相机的分辨率变为原来的n倍而其他地方不变，那么它的内参也将变为原来的n倍