基于一阶互补滤波的MPU6050姿态解算

之前报名了第十八届全国大学生智能车竞赛的单车越野组别，但由于种种原因最终未能完赛。所以打算把自己做好的一部分发出来，希望对往后的刚参加竞赛的同学们有所帮助，同时也是对自己过去一个多学期生活的一点总结。由于学疏才浅，如有不准确或者错误的地方，还请不吝赐教。

代码基于逐飞科技的CH32V307开源库。

为什么需要一阶互补滤波

当我们通过MPU6050进行姿态解算时，MPU6050给了我们两组数据：一组来自加速度计，一组来自陀螺仪。两个传感器的数据都可以独自求得小车此时的角度，但它们也各自存在问题：加速度计比较敏感，由振动产生的瞬时误差比较大；陀螺仪积分得到的角度虽然受振动影响比较小，但随着时间的增加，积分误差和温度漂移会逐渐增大。从另一角度加以解释，就是加速度计主要受到高频噪声的影响，而陀螺仪主要受到低频噪声的影响。这两个传感器正好可以弥补相互的缺点。短时间用陀螺仪比较准确，长时间用加速度计比较准确；运动时用陀螺仪比较准确，静止时用加速度计比较准确，也就是互补。通过一阶互补滤波，我们滤除加速度计的高频部分，滤除陀螺仪的低频部分，并将这两个数据以一定权重相加，就能得到比较准确的角度了。

你能在其他资料里面看到二阶互补滤波和卡尔曼滤波。相比于这两种算法，一阶互补滤波的优势在于计算量少、收敛速度较快，对性能薄弱的芯片比较友好。虽然没有二阶互补滤波和卡尔曼滤波那么精确，但是对于我们的用途来说还在能接受的范围以内。

下面我们结合代码来说明基于一阶互补滤波的姿态解算的流程。

自定义结构体

为了让代码看起来更加优雅，我们先定义这样一个结构体，并且声明对应的变量，来储存我们需要的数据。

typedef struct{float Roll;//解算所得角度float Pitch;float Yaw;float Roll_a;//加速度计计算得到的角度float Pitch_a;float Roll_g;//陀螺仪计算得到的角速度float Pitch_g;float lastRoll;//上次的解算角度float lastPitch;int offset_gx;//陀螺仪零漂值int offset_gy;int offset_gz;
}IMU;...IMU IMU_Data;

加速度计与陀螺仪的分别解算

在这里我们以小车的Roll角（翻滚角），也就是单车需要保持平衡的那个角度为例，来解释如何通过加速度计与陀螺仪分别计算出角度。额外注意的是，本文的X轴指向小车前方，如下图所示，但别的资料不一定，在查阅其他资料时请多加留心。

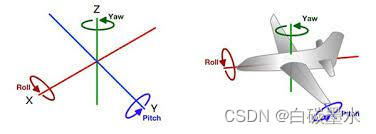
加速度计

IMU_Data.Roll_a=atan2(mpu6050_acc_x,mpu6050_acc_z)/(PI/180);

对数学上的推导过程感兴趣的朋友可以参考这篇博客，在这里不展开说明。总之，mpu6050_acc_x与mpu6050_acc_z是我们通过逐飞库提供的mpu6050_get_acc函数读取到的直接数据，通过上面的数学运算，我们得到的是根据加速度计算得的Roll角Roll_a，单位为度。atan2函数定义在math.h标准库中，使用前要先包含这个库。

如果要计算Pitch角（俯仰角），只需要把x改为y即可。遗憾的是，由于原理上的限制，我们无法用加速度计算出Yaw角（航向角）。

陀螺仪

IMU_Data.Roll_g=-(mpu6050_gyro_y)/14.3;

通过这个运算，我们能把MPU6050提供的陀螺仪数据转换成实际的物理数据，单位是度每秒，也就是角速度。我们只需要对角速度进行积分，就能得到角度了，这个处理我们放在一阶互补滤波的函数中。代码中是否要加负号取决于你的传感器芯片，14.3这个数字由陀螺仪的量程得出，如果用逐飞库的mpu6050_gyro_transition函数来转换的话应该就不用关心这个数字了。

同样的，如果要计算Pitch角，只需要把y改为x即可。你甚至可以用Z轴的数据算出Yaw角，不过，就像我们上面提到的，随着时间的推移，误差将不断增大。要弥补这一误差，你可以结合GNSS（全球卫星导航系统）的数据，但这不在本文的讨论范围之内。

一阶互补滤波过程

#define Ka 0.80  //加速度解算权重
#define dt 0.005 //采样间隔（单位：秒）float FOCF(float acc_m,float gyro_m,float* last_angle){float temp_angle;temp_angle=Ka*acc_m+(1-Ka)*(*last_angle+gyro_m*dt);*last_angle=temp_angle;return temp_angle;
}...IMU_Data.Roll=FOCF(IMU_Data.Roll_a,IMU_Data.Roll_g,&IMU_Data.lastRoll);

在分别处理好加速度计与陀螺仪的数据之后，现在要将两个数据互补在一起。我们定义一个名为FOCF的函数，用于处理这一数学过程。这个函数接受处理好的数据和上次解算结果的储存地址作为参数。

首先，我们将陀螺仪解算出的角速度与采样间隔相乘，得到自上次采样以来的角度变化量。通过将上一次解算结果与这个变化量相加，我们就能得到由陀螺仪计算得到的新的Roll角。

接着，我们将加速度解算所得的角度与陀螺仪解算所得的角度按照权重因子进行加权相加，从而得到最终的解算结果。这个权重因子需要根据实际情况进行调整。

在计算完成后，我们更新*last_angle，以备下一次解算使用。最终，将计算得到的角度作为结果返回，你就能在其他函数中读取IMU_Data.Roll，最终保持你的单车的平衡。

Pitch角也是同理。

在解算之前......

不幸的，你接上陀螺仪后发现，即使你不去触动它，它的数据也不为0，这是工艺上不可避免的误差造成的。幸运的是，这个误差在每一次运行过程中变化不大，让我们可以用简单的方法把它的影响降到最小。

现在我们定义一个去除零漂的函数IMU_offset，并在每次单片机启动时调用它。

#define OFFSET_COUNT 200void IMU_offset(){for(int i=0;i<OFFSET_COUNT;i++){system_delay_ms(5);if(mpu6050_gyro_x==mpu6050_gyro_y){i--;}else{IMU_Data.offset_gx+=mpu6050_gyro_x;IMU_Data.offset_gy+=mpu6050_gyro_y;IMU_Data.offset_gz+=mpu6050_gyro_z;}}IMU_Data.offset_gx/=OFFSET_COUNT;IMU_Data.offset_gy/=OFFSET_COUNT;IMU_Data.offset_gz/=OFFSET_COUNT;
}

既然变化不大，我们只需要求其平均值，然后在每次采样时减去它就好了。这个函数就起求平均值这个作用。OFFSET_COUNT是你要采集的数据量，只要取一个恰当的数值即可。system_delay_ms(5)中的5是你规定的采样间隔。

考虑到实际应用中有时会出现杜邦线接触不良的情况，在代码中做了一个简单的判断。当发生接触不良的时候，X轴数据会与Y轴数据相同（通常均为0，但偶有意外），我们就认为数据是无效的。这是在被杜邦线困扰已久之后摸索出的野路子，权当参考。

综上所述

当我们完成了上面所有的代码之后，是时候调用它们了。去零漂的函数要在启动时调用，也就是main函数的开头部分。为了保证我们的采样间隔恒定不变，我们需要将函数放在定时器的中断处理函数中执行。代码分为两个部分：第一个部分你要从MPU6050中读取原始的数据，并将陀螺仪的原始数据减去你计算出的零漂值；第二个部分你要分别处理加速度计与陀螺仪的数据，然后进行一阶互补滤波。

上面就是基于一阶互补滤波的姿态解算的全部过程，希望能对同学们有所帮助。

（感觉这玩意各种意义上都写得好烂......）