本文主要是介绍【博士每天一篇论文-算法】Optimal modularity and memory capacity of neural reservoirs,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
阅读时间:2023-11-15
1 介绍
年份:2019
作者:Nathaniel Rodriguez 印第安纳大学信息学、计算和工程学院,美国印第安纳州布卢明顿
期刊: Network Neuroscience
引用量:39
这篇论文主要研究了神经网络的模块化与记忆性能之间的关系,提出记忆性能存在一个最佳模块化程度,即在局部凝聚性和全局连接性之间建立平衡。这种最佳模块化可以使神经网络具有更长的记忆能力。
作者提出从神经网络的动力学分析和信息传播过程中获取的见解可以用于更好地设计神经网络,并可以揭示大脑的模块化组织。
研究了基于信息扩散和储备计算机的模块化的作用,展示了这对于平衡局部和全局通信和计算的能力以及提高记忆性能的效果。
2 创新点
(1)揭示了记忆性能的最佳模块化结构
通过研究神经网络的结构组织如何影响其功能能力,发现在记忆性能方面存在一个最佳的模块化结构。这个最佳模块化结构在局部凝聚性和全局连接性之间实现了平衡,从而使神经网络能够具有更长的记忆能力。
(2)动力学分析和信息传播过程揭示了设计神经网络的见解
作者提出了通过神经网络的动力学分析和信息传播过程来更好地设计神经网络的方法,并提出这种方法可能为大脑的模块化组织提供见解。通过基于信息扩散理论的模块化角色的研究,作者探讨了模块化在储层计算机中的作用。
(3)ESN中的社区的作用
通过研究信息扩散理论和模块化对预留河计算机的影响,作者发现ESN中的社区可以在局部和全局通信和计算之间提供平衡的方式,从而提高记忆性能。
3 相关研究
(1)储层计算(Reservoir computers)是生物学上可行的大脑计算模型
【Reservoir computing properties of neural dnamics in prefrontal cortex】
【Minimal approach to neuro-inspired information processing】
(2)储层计算与RNN不同,储层计算仅训练少量输出参数,而不是训练所有连接参数。储层计算机利用神经储层的隐式计算能力-模型神经元的网络。
储层计算机学习特定行为的能力取决于储层的动力学集合的丰富程度。
【Reservoir computing approaches to recurrent neural network training】
【A neurodynamical model for working memory】
(3)在ESN中受多个因素的影响,包括谱半径(the spectral radius )、输入和储层权重尺度( reservoir weight scales)以及储层大小( reservoir size)。
在记忆任务中,性能在谱半径的临界点附近急剧增加,嵌入在具有长转换和前一输入回响神经元状态的动力学区域,保存了过去的信息。【A neurodynamical model for working memory】【An experimental unification of reservoir computing methods】发现权重分布在性能方面也起重要作用。【Effects of synaptic connectivity on liquid state machine performance】
(4)储层拓扑的影响有较多的研究
使用小世界【Collective behavior of a small-world recurrent neural system with scale-free distribution.】, scale-free【 Collective behavior of a small-world recurrent neural system with scale-free distribution】,columnar 【Effects of synaptic connectivity on liquid state machine performance】【.A priori data-driven multi-clustered reservoir generation algorithm for echo state network-2015】,Kronecker图【An approach to modeling networks-2010】和带有横向抑制的集合【Decoupled echo state networks with lateral inhibition】,每种方法的性能都优于简单的随机图。
4 实验分析
4.1 验证线性阈值模型中发现的最优模块化现象是否适用于神经
通过两个模拟实验,验证了最优模块化现象不仅适用于线性阈值模型,也可以推广到神经网络中的沉积池。实验结果表明,当网络中的模块连接强度适中时,可以实现最大激活效果,优化整个网络的响应。
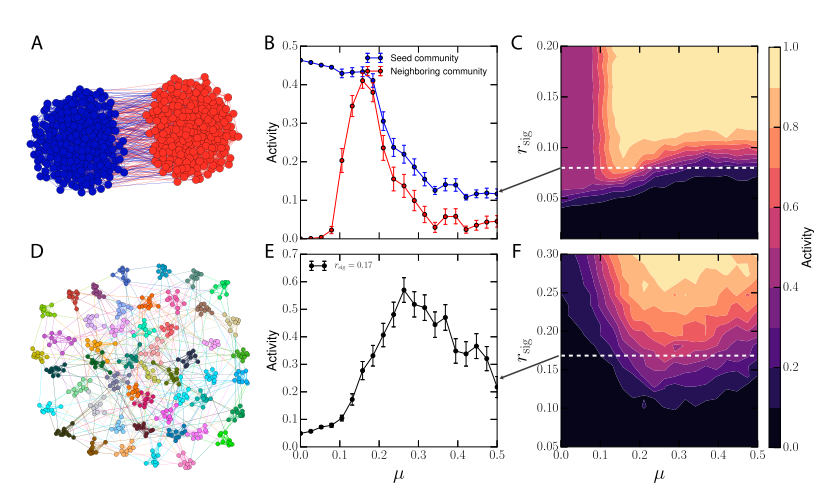
(1)第一个实验使用了一个简单的双社区配置,其中桥梁比例μ控制网络中的社区结构强度。当μ=0时,社区之间完全隔离,社区结构最强;当μ≈0.5时,社区之间连接最多。实验结果显示,即使没有指定种子社区,类似的最优模块化行为仍然存在。在低μ值下,由于缺乏桥梁的存在,输入信号无法得到加强,即使是高度凝聚的社区也无法被激活。在高μ值下,虽然存在许多全局桥梁有助于巩固信号,但局部凝聚度不足以维持强烈的响应。在最优区域,社区的放大效应与桥梁的全局传播之间存在平衡,使得网络能够将亚临界的、全局分布的信号传播到整个网络。然而,在线性和双曲正切的库中,并未发现这种关系。
(2)第二个实验模拟一个具有许多社区的网络,这些社区类似于ESN(Echo State Network)或大脑中观察到的社区。与之前的研究仅仅考虑输入到单个社区不同,这里扩展到了多个社区。实验结果显示,即使没有指定的种子社区,类似的最优模块化行为也出现。在低μ值下,由于缺乏桥梁的存在,输入信号无法得到加强,甚至无法激活高度凝聚的社区。在高μ值下,许多全局桥梁有助于巩固信号,但局部凝聚度不足以维持强烈的响应。在最优区域中,社区的放大效应与桥梁的全局传播之间存在平衡,使得网络能够将亚临界、全局分布的信号传播到整个网络。然而,在线性和双曲正切的库中,并未发现这种关系。
4.2 最优模块化对神经网络记忆能力的影响
通过Jaeger(2002)开发的常见的记忆基准任务。【Short term memory in echo state networks】
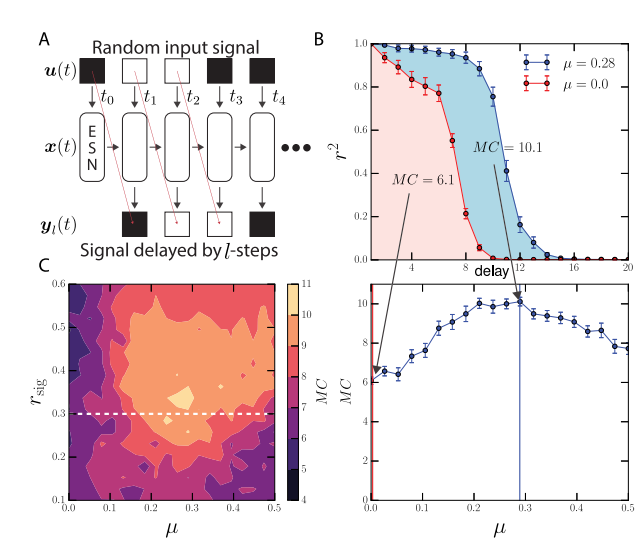
在记忆任务中,研究了最优模块化对神经网络记忆能力的影响。结果发现,当网络模块化结构较强时,网络的记忆能力较差。随着模块之间的连接增强,网络的记忆性能显著改善,但当连接过于密集时,会导致性能下降。模块化会降低记忆容量,因为社区创建了信息瓶颈。然而,权重尺度(weight-scales)在ESN中能平衡这个性能。使用输入信号与延迟输出信号之间的二项分布的决定系数来量化ESN的性能。网络的记忆容量是在所有时间延迟下的这些性能之和。MC是网络的记忆容量。
4.3 记忆任务中的模块化结构对性能的影响
引入一个召回任务,在网络中输入随机生成的二进制序列,并通过网络的吸引子(Attractors)空间来存储并召回这些序列。发现模块化网络在性能上表现更好,并且在μ约为0.1时达到最佳性能。此外,模块化网络具有更多的可用吸引子,而过度互连会导致吸引子数量减少。在适度的模块化结构下,网络具有更多的可用吸引子,有利于提高网络的信息存储能力。然而,过多的连接会将各个初始状态牵扯到少数几个大吸引子中,导致性能下降。
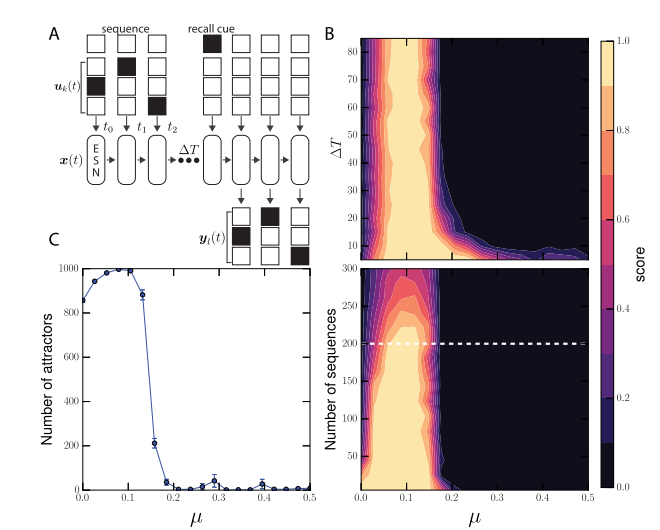
吸引子表示网络在记忆和召回过程中所处的特定状态。吸引子提供了一种稳定的状态,使得网络可以存储和恢复信息。
5 代码
https://github.com/Nathaniel-Rodriguez/reservoirlib
6 思考
作者从多个角度去分析了模块化结构对于类脑网络ESN的影响。此外模块化结构还有助于在噪声环境、学习新技能和处理系统建模等方面提高神经网络的性能。
作者用两种方法去评价模型的记忆能力和信息存储能力,分别是MC和Attractors方法。本文比较新颖的提出了用Attractors去评价模型的记忆存储能力。MC方法适用于不依赖于具体系统模型的性能评估,而Attractors方法则适用于需要考虑系统动力学特性的性能评估。
这篇关于【博士每天一篇论文-算法】Optimal modularity and memory capacity of neural reservoirs的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









