【矩阵论】特征值的估计(上下界和盖尔圆)

本文主要是介绍【矩阵论】特征值的估计(上下界和盖尔圆)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言：为什么不直接求特征值而是去估计特征值？

当我们遇到的不是书本上的3阶或4阶矩阵，而是高阶矩阵时(如图像中的256×256)，我们再使用特征方程$\det (\lambda I-A)=0$来求特征值就非常困难。我们难以求解也没有必要逐一计算每一个精确的特征值。因此，在实际工程计算上，面对高阶矩阵，我们常常通过计算特征值的范围来估计特征值，这个范围越小，所估计的特征值就越精确。以下，本文就特征值估计常用方法做以梳理，完整定理证明请参考西工大的《矩阵论》[1]。

思路：如何估计特征值？

我们知道，对于$n$阶非奇异方阵，有$n$个特征值。

• 从粗粒度的思路出发，我们可以先确定整体特征值(${\lambda }_1,...,{\lambda }_n$)的上下界，对于复数域的矩阵，我们还需要分别考虑其特征值的实部和虚部，这就像我们找犯罪嫌疑人需要先知道TA的性别、身高以及一些宽泛的特征从而对TA有个大致的定位。
• 从细粒度的思路出发，我们可以更深入的确定每个特征值${\lambda }_i$的范围，如果这些范围有重叠，比如两个嫌疑人有一些共同特征，那对我们来说也是件麻烦事，但我们可以通过相似矩阵具有相同特征值的特点设计对角阵来按比例缩放每个特征值的范围。

梳理以上的两个朴素的idea，我们可以得到如下解决方案

一、特征值的界

我们主要的目的是仅通过计算原矩阵中的每个元素即可得到特征值的上下界。

方法1计算特征值虚部的上界($M$越小，虚部$\text{Im}(\lambda )$越小)

设$A=(a_{ij})\in {\mathbb{R}}^{n\times n}$，若$\lambda$表示$A$的任一特征值，则$\lambda$的虚部$\text{Im}(\lambda )$满足如下不等式
$$\{\begin{array}{l}M={\max }_{1\le i,s\le n}\frac{1}{2}|a_{ij}-a_{ji}|\\ |\text{Im}(\lambda )|\le M\sqrt{\frac{n(n-1)}{2}}\end{array}\text{\hspace{1em}(1.1)}$$

方法2计算特征值、实部和虚部的上界(该法虚部估计误差比法1大)

设$A=(a_{ij})\in {\mathbb{C}}^{n\times n}$，若$\lambda$表示$A$的任一特征值，则有

$$\{\begin{array}{l}|\lambda |\le \Vert A{\Vert }_{m_{\infty }}=n\cdot {\max }_{i,j}|a_{ij}|\\ |\text{Re}(\lambda )|\le \frac{1}{2}\Vert A+A^H{\Vert }_{m_{\infty }}\\ |\text{Im}(\lambda )|\le \frac{1}{2}\Vert A-A^H{\Vert }_{m_{\infty }}\end{array}\text{\hspace{1em}(1.2)}$$

方法3计算矩阵行列式($n$个特征值乘积)的上下界(需满足严格对角占优)

【预备知识】：设$A=(a_{ij})\in {\mathbb{C}}^{n\times n},R_r(A)={\sum }_{s=1,s\ne r}^n|a_{rs}|$，若所有$|a_{rr}|>R_r$，则称矩阵$A$按行严格对角占优。若存在某$|a_{rr}|\ge R_r$且至少有一个$|a_{rr}|>R_r$则成为按行(弱)对角占优。例如

$$\begin{array}{c}A=\left[\begin{array}{ccc}9& 2& 3\\ 5& 9& 1\\ 1& 1& -9\end{array}\right]\end{array}\begin{array}{c}B=\left[\begin{array}{ccc}9& 2& 3\\ 4& 9& 5\\ 1& 8& -9\end{array}\right]\end{array}$$
则由于
$$\{\begin{array}{l}9=|a_{11}|>R_1(A)=|a_{12}|+|a_{13}|=5\\ 9=|a_{22}|>R_2(A)=|a_{21}|+|a_{23}|=6\\ 9=|a_{33}|>R_3(A)=|a_{31}|+|a_{32}|=2\end{array}\{\begin{array}{l}9=|b_{11}|>R_1(B)=5\\ 9=|b_{22}|\ge R_2(B)=9\\ 9=|b_{33}|\ge R_3(B)=9\end{array}$$
可知矩阵$A$按行严格对角占优，而矩阵$B$按行(弱)对角占优。
【定理】：设$A=(a_{ij})\in {\mathbb{C}}^{n\times n}$，若$A$按行严格对角占优，则有如下不等式

$$\{\begin{array}{l}{M}_r=|a_{rr}|+{\sum }_{s=r+1}^n|a_{rs}|\\ m_r=|a_{rr}|-{\sum }_{s=r+1}^n|a_{rs}|\end{array}$$

$$0<\prod _{r=1}^n{m}_r\le |\det A|=\prod _{r=1}^n{\lambda }_r(A)\le \prod _{r=1}^n{M}_r\text{\hspace{1em}(1.3)}$$

方法4计算矩阵特征值模的平方和的上界($\text{Schur}$不等式)

设$A=(a_{ij})\in {\mathbb{C}}^{n\times n}$的特征值为${\lambda }_1,...,{\lambda }_n$，则有如下不等式
$$\begin{gathered} \Vert \lambda {\Vert }_2^2=\sum _{i=1}^n|{\lambda }_i{|}^2\le \sum _{i=1}^n\sum _{j=1}^n|a_{ij}{|}^2=\Vert A{\Vert }_F^2 \\ \text{\hspace{1em}(1.4)} \end{gathered}$$

二、特征值的包含区域

此处主要通过$\text{Gerschorin}$圆(盖尔圆)理论来划分特征值区域，盖尔圆的应用主要在于隔离特征值，该理论力求将每个特征值隔离到一个较小的范围内。

2.1 什么是$\text{Gerschorin}$圆(盖尔圆)？

【定义】设$A=(a_{ij})\in {\mathbb{C}}^{n\times n}$，则称矩阵$A$的第$i$个$\text{Gerschorin}$圆(盖尔圆)是由如下不等式在复平面上确定的区域。
$$G_i:|z-a_{ii}|\le R_i\text{\hspace{1em}(2.1)}$$
其中，如下称为盖尔圆$G_i$的半径
$$R_i=R_i(A)=\sum _{j=1,j\ne i}^n|a_{ij}|$$

2.2 $\text{Gerschorin}$圆(盖尔圆)的主要性质有哪些？

• 【性质1】矩阵$A=(a_{ij})\in {\mathbb{C}}^{n\times n}$的一切特征值都在它的$n$个盖尔圆的并集之内。
• 【性质2】在矩阵$A$的所有盖尔圆组成的任一连通部分中，含有$A$的特征值的个数等于该连通部分的盖尔圆的个数。(连通区域：区域中的任一两点都可以用位于该区域内的一条折线连接起来)
• 【性质3】设$A=(a_{ij})\in {\mathbb{C}}^{n\times n},B=(a_{ij})\in {\mathbb{R}}^{n\times n}$，若$b_{ij}\ge |a_{ij}|(i,j=1,..,n)$，则对$A$的任一特征值$\lambda$必有$i$，使得 [$\rho (B)$表示$B$的谱半径]
  $$b_{ij}\ge |a_{ij}|\Rightarrow |\lambda -a_{ii}|\le \rho (B)-b_{ii}$$
• 【性质4】设$A=(a_{ij})\in {\mathbb{C}}^{n\times n}(n\ge 2)$，如果对于所有$i\ne j$，恒有
  $$|a_{ii}||a_{jj}|>R_i(A)R_j(A)\iff \det A\ne 0$$

2.3 放缩$\text{Gerschorin}$圆(盖尔圆)的对角阵如何取？

由相似矩阵具有相同特征值的性质，常用如下关系放缩矩阵$A$的特征值盖尔圆
$$B=DA{D}^{-1}$$

对于对角阵$D$的选取，我们常用如下准则

• 放大第$i$个盖尔圆，则取$d_i>1$，其余$d_j=1(j\ne i)$.
• 缩小第$i$个盖尔圆，则取$d_i<1$，其余$d_j=1(j\ne i)$.
• 用来放缩的$d_i\ne 1$，直接作用于$A$的第$i$行的非主对角元素，$1/d_i$作用于$A$的第$i$列的非主对角元素.

当放缩第$i$个盖尔圆的同时也会一定程度放缩其他盖尔圆，例如有如下矩阵$A$
$$\begin{array}{c}A=\left[\begin{array}{ccc}20& 3& 1\\ 2& 10& 2\\ 8& 1& 0\end{array}\right]\end{array}$$
分别取$D_1$和$D_2$如下
$$\begin{array}{c}{D}_1=\left[\begin{array}{ccc}2& & \\ & 1& \\ & & 1\end{array}\right]D_2=\left[\begin{array}{ccc}1& & \\ & 1& \\ & & \frac{1}{2}\end{array}\right]\end{array}$$
由$B=DA{D}^{-1}$得
$$\begin{array}{c}{B}_1=\left[\begin{array}{ccc}20& 6& 2\\ 1& 10& 2\\ 4& 1& 0\end{array}\right]B_2=\left[\begin{array}{ccc}20& 6& 2\\ 2& 10& 4\\ 4& 0.5& 0\end{array}\right]\end{array}$$
可见
$$\begin{gathered} 行：b_{ik}=d_i\times a_{ik}(i\ne k) \\ 列：b_{ki}=\frac{1}{d_i}\times a_{ki}(i\ne k) \end{gathered}$$

2.4 $\text{Gerschorin}$圆(盖尔圆)的应用(习题)

2.4.1 利用盖尔圆求每个特征值的范围

2.4.2 利用盖尔圆隔离范围重叠的特征值

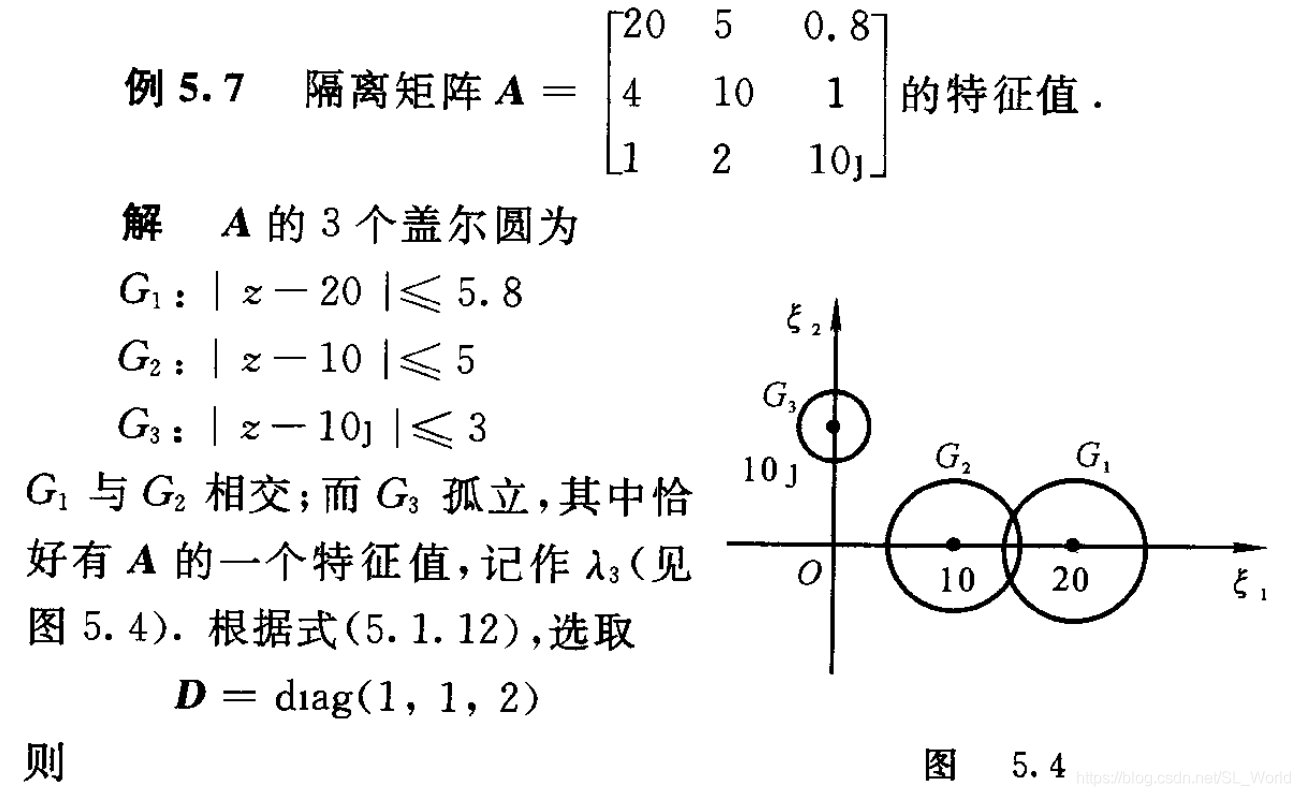
2.4.3 利用盖尔圆性质3计算特征值范围

【问题】估计如下矩阵的特征值范围
$$\begin{array}{c}A=\left[\begin{array}{cc}1& -0.8\\ 0.5& 0\end{array}\right]\end{array}$$
【解】由性质3得
$$b_{ij}\ge |a_{ij}|\Rightarrow |\lambda -a_{ii}|\le \rho (B)-b_{ii}$$
因此构造一个满足比矩阵$A$每个元素都大于等于的矩阵$B$
$$\begin{array}{c}B=\left[\begin{array}{cc}1& 1\\ 1& 1\end{array}\right],则\left|\begin{array}{cc}\lambda -1& -1\\ -1& \lambda -1\end{array}\right|=(\lambda -1{)}^2-1=\lambda (\lambda -2)\end{array}$$
得${\lambda }_1=0,{\lambda }_2=2$，所以$\rho (B)=\max ({\lambda }_1,{\lambda }_2)=2$，因此$A$的特征值至少满足一下不等式之一
$$\{\begin{array}{l}|\lambda -1|\le 2-1=1\\ |\lambda -0|\le 2-1=1\end{array}$$

2.4.4 利用盖尔圆性质4判别矩阵奇异性

$$|a_{ii}||a_{jj}|>R_i(A)R_j(A)\iff \det A\ne 0$$

附录1：特征值的界—习题

例1-求特征值上界估计如下矩阵特征值的上界
$$\begin{array}{c}A=\left(\begin{array}{cc}1& -0.8\\ 0.5& 0\end{array}\right)\end{array}$$
解：①应用方法1
$$\{\begin{array}{l}M=\max \frac{1}{2}|1.3|=0.65\\ |\text{Im}(\lambda )|\le M\sqrt{\frac{n(n-1)}{2}}=0.65\cdot \sqrt{\frac{2(2-1)}{2}}=0.65\end{array}\text{\hspace{1em}(1.1)}$$
②应用方法2
$$\{\begin{array}{l}|\lambda |\le \Vert A{\Vert }_{m_{\infty }}=n\cdot {\max }_{i,j}|a_{ij}|=2\cdot 1=2\\ |\text{Re}(\lambda )|\le \frac{1}{2}\Vert A+A^H{\Vert }_{m_{\infty }}=\frac{1}{2}(2\cdot 2)=2\\ |\text{Im}(\lambda )|\le \frac{1}{2}\Vert A-A^H{\Vert }_{m_{\infty }}=\frac{1}{2}(2\cdot 1.3)=1.3\end{array}\text{\hspace{1em}(1.2)}$$
可见方法1在计算特征值虚部上界中比方法2更精准。

例2-求模最小特征值上界估计如下矩阵按模最小特征值的上界
$$\begin{array}{c}A=\left(\begin{array}{cc}1& -0.8\\ 0.5& 1\end{array}\right)\end{array}$$
解：分析该问题的矩阵，我们不难发现矩阵$A$按行严格对角占优，因此可应用方法3快速求解
首先计算$M_1=1.8,M_2=1$，因此有
$$\begin{array}{rl}& \prod _{r=1}^n{\lambda }_r(A)\le \prod _{r=1}^n{M}_r=1.8\\ \Rightarrow & ({\lambda }_{\min }{)}^2\le {\lambda }_1\cdot {\lambda }_2=1.8\\ \Rightarrow & {\lambda }_{\min }\le \sqrt{1.8}\end{array}$$
而实际情况，$|{\lambda }_{1,2}|=\sqrt{1.4}$。

例3-部分特征值上界已知如下矩阵的一个特征值${\lambda }_1=2$，估计另外两个特征值的上界
$$\begin{array}{c}A=\left(\begin{array}{ccc}3+i& -2-3i& 2i\\ 1& 0& 0\\ 0& 1& 0\end{array}\right)\end{array}$$
解：分析该问题的矩阵，我们发现矩阵$A$并不是按行严格对角占优，因此无法用方法3求解
，可用方法4求解，因此有
$$\begin{array}{rl}\sum _{i=1}^n|{\lambda }_i{|}^2=4+|{\lambda }_2{|}^2+|{\lambda }_3{|}^2& \le \sum _{i=1}^n\sum _{j=1}^n|a_{ij}{|}^2=\Vert A{\Vert }_F^2\\ & =9+|i^2|+4+|9i^2|+|4i^2|+1+1\\ & =29\\ \Rightarrow |{\lambda }_2{|}^2+|{\lambda }_3{|}^2& \le 25\\ \Rightarrow |{\lambda }_{1,2}|& \le 5\end{array}$$

附录2：特征值的界—相关定理证明

方法2引理证明 设$B\in {\mathbb{C}}^{n\times n}$，列向量$y\in {\mathbb{C}}^n$满足$\Vert y{\Vert }_2=1$，则
$$|y^{H}By|\le \Vert B{\Vert }_{m_{\infty }}$$
【证明】：设$B=(b_{ij})\in {\mathbb{C}}^{n\times n},y=({\eta }_1,...,{\eta }_n{)}^T$，于是有
$$\begin{array}{rl}|y^{H}By|& =|\sum _{i,j=1}^n{\bar{\eta }}_i{b}_{ij}{\eta }_j|\le \underset{i,j}{\max }|b_{ij}|\cdot \sum _{i,j=1}^n|{\eta }_i||{\eta }_j|\\ & \le \underset{i,j}{\max }|b_{ij}|\cdot \frac{1}{2}\sum _{i,j=1}^n(|{\eta }_i{|}^2+|{\eta }_j{|}^2)(a^2+b^2\ge 2|ab|)\\ & =\underset{i,j}{\max }|b_{ij}|\cdot \frac{1}{2}(\sum _{j=1}^n\Vert y{\Vert }_2^2+\sum _{i=1}^n\Vert y{\Vert }_2^2)\\ & =\underset{i,j}{\max }|b_{ij}|\cdot \frac{1}{2}(n+n)=\Vert B{\Vert }_{m_{\infty }}\end{array}$$

方法2证明
$$\{\begin{array}{l}|\lambda |\le \Vert A{\Vert }_{m_{\infty }}\\ |\text{Re}(\lambda )|\le \frac{1}{2}\Vert A+A^H{\Vert }_{m_{\infty }}\\ |\text{Im}(\lambda )|\le \frac{1}{2}\Vert A-A^H{\Vert }_{m_{\infty }}\end{array}$$
【证明】：令$x\in {\mathbb{C}}^{n\times 1}$是$A$的属于特征值$\lambda$的单位特征向量，即$Ax=\lambda x$且$x^{H}x=I$，由瑞利商理论得$\lambda =x^{H}Ax$且$\bar{\lambda }=x^H{A}^{H}x$.由方法2引理得
$$\begin{gathered} |\lambda |=|x^{H}Ax|\le \Vert A{\Vert }_{m_{\infty }} \\ |\text{Re}(\lambda )|=\frac{1}{2}|\lambda +\bar{\lambda }|=\frac{1}{2}|x^H(A+A^H)x|\le \frac{1}{2}\Vert A+A^H{\Vert }_{m_{\infty }} \\ |\text{Im}(\lambda )|=\frac{1}{2}|\lambda -\bar{\lambda }|=\frac{1}{2}|x^H(A-A^H)x|\le \frac{1}{2}\Vert A-A^H{\Vert }_{m_{\infty }} \end{gathered}$$

参考文献

程云鹏, 凯院, 仲. 矩阵论[M]. 西北工业大学出版社, 2006.

这篇关于【矩阵论】特征值的估计(上下界和盖尔圆)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---