下界专题
stl-二分找上下界
下面介绍两个函数用来查找一个有序序列关键字的上下界 upper_bound返回第一个大于的元素的下标； lower_bound返回第一个大于或等于元素的下标； 代码如下： #include<stdio.h>#include<algorithm>using namespace std;int main(){int data[10] ={0,1,1,2,2,2,2,3,4,7};//u
【无源汇的上下界网络流】【模板】
上界改容量，下界先流走。 U -> V之间添加一条 cap - down的边 S->U 为U多出来的入的下界- 出的下界 V -> T 为V多出来的出的下界-入的下界 Max_Flow<int> MF;int n,m;const int maxn = 210;const int maxm = 40010;int a[maxn];int id[maxm];int up
Scala的协变covariant(+)，逆变contravariant(-)，上界(:)，下界(:)
原文：https://my.oschina.net/xinxingegeya/blog/486671 Scala的协变(+)，逆变(-)，上界(<:)，下界(>:) 协变covariant、逆变contravariant、不可变invariant 对于一个带类型参数的类型，比如 List[T]，如果对A及其子类型B，满足 List[B]也符合List[A]的子类型，那么就称为covar
poj 2396 zoj 1994 Budget（有源汇上下界的可行流）
思路： 无源汇 (附加源汇+最大解决) 有源汇 (附加(T,S)->无源汇) Budget Time Limit: 3000MS Memory Limit: 65536KTotal Submissions: 6237 Accepted: 2367 Special Judge Description We are supposed to make
Scala 入门-泛型，上界，下界
专栏原创出处：github-源笔记文件 ，github-源码 ，欢迎 Star，转载请附上原文出处链接和本声明。 Scala 编程语言专栏系列笔记，系统性学习可访问个人复盘笔记-技术博客 Scala 编程语言 什么是泛型类 泛型类指可以接受类型参数的类，在 类名 后 + [类型参数 ],例如：class Stack[A]。 泛型类在集合类中被广泛使用，例如 Scala 集合的 Li
zoj2314 Reactor Cooling --- 上下界可行流
题目给出了每条边的上下界， 此类题目的建边方法是： 1、添加源点汇点， 2、对每条边 添加边 c(u,v) = up(u,v) - low(u,v) 3、对每个点 c(s,v) = out(v) c(v,t) = in(v) (权值为正) 求s到t的最大流，若最大流等于所有边下界的和，则存在可行流， 每条边的流量为 flow(u
两正序列元素之和比值的上下界——小于等于其元素之比的最大值，大于等于元素之比的最小值
对于两个正数序列（集合） { a 1 , a 2 , . . . , a l } \{a_1,a_2,...,a_l\} {a1,a2,...,al} 和 { b 1 , b 2 , . . . , b l } \{b_1,b_2,...,b_l\} {b1,b2,...,bl} ，满足 min i a i b i ≤ ∑ i = 1 l a i ∑ i = 1 l b i ≤
STL库查找算法——如上下界查找，最大最小值查找，统计次数，二分查找，子区间匹配查找，集合（集合内任意一个元素匹配）查找
STL中有很多算法，这些算法可以用到一个或多个STL容器（因为STL的一个设计思想是将算法和容器进行分离），也可以用到非容器序列比如数组中。众多算法中，查找算法是应用最为普遍的一类。 以下算法参数均可以迭代器或指针。 单个元素查找 1、 find() 比较条件为元素是否相等的查找： 1 2 template <class InputIterator, class T> InputIte
Scala泛型、隐式转换和隐式参数、视图介绍、Scala中的上界、下界、结合柯里化进行隐式转换
二、泛型 一、Scala泛型 1. 泛型介绍 泛型用于指定方法或类可以接受任意类型参数，参数在实际使用时才被确定，泛型可以有效地增强程序的适用性，使用泛型可以使得类或方法具有更强的通用性。泛型的典型应用场景是集合及集合中的方法参数，可以说同java一样，scala中泛型无处不在，具体可以查看scala的api。 2. 泛型类、泛型方法 泛型类：指定类可以接受任意类型参数。 泛型方法：指
hdoj 1597 二分 下界（等差数列）
题目链接 MAX根据题目 n(n+1)/2 = INT_MAX 估计出来的 #include<iostream>#include<cmath> #include<limits.h>#include<string.h>#include<algorithm>#define MAX 66000using namespace std;int k, n;int g, t;
Codeforces TypeDB Forces 2023 C. Remove the Bracket【上下界DP】
C. Remove the Bracket 题意 给定一个长度为 n n n 的整数数组 a a a 和一个非负整数 s s s 要求 ∀ i ∈ [ 2 , n − 1 ] , 选定两个整数 x i , y i ，满足 x i + y i = s 且 ( x i − s ) ( y i − s ) ≥ 0 \forall i \in [2,n - 1],选定两个整数 x_i,
详解二分法查找目标值/二分法查找上下界的两种写法
本文中默认数组呈升序。 💡 绝对不能使用left = cur这种更新，由于整数除法取下界，left不更新会导致循环无法结束 寻找与target相等 可以用(l < r)写法，末尾r==l需要检查是否满足条件，满足则输出，不满足则输出-1可以用(l<=r) 写法，末尾输出r 不需要检查是否满足条件，不满足的情况下r为-1，因此结果r可能会超出数组索引，注意不要对此进行nums[r]的检查
Scala第十六章节(泛型方法, 类, 特质的用法、泛型上下界、协变, 逆变, 非变的用法以及Scala列表去重排序案例)
Scala第十六章节 章节目标 掌握泛型方法, 类, 特质的用法了解泛型上下界相关内容了解协变, 逆变, 非变的用法掌握列表去重排序案例 1. 泛型 泛型的意思是泛指某种具体的数据类型, 在Scala中, 泛型用[数据类型]表示. 在实际开发中, 泛型一般是结合数组或者集合来使用的, 除此之外, 泛型的常见用法还有以下三种: 泛型方法泛型类泛型特质 1.1 泛型方法 泛型方法指的
排序算法的时间复杂度存在下界问题
对于几种常用的排序算法，无论是归并排序、快速排序、以及更加常见的冒泡排序等，这些排序算法的时间复杂度都是大于等于O(n*lg(n))的，而这些排序算法存在一个共同的行为，那就是这些算法在对元素进行排序的时候，都会进行同一个操作，也就是对数组中取出文件，然后会对取出来的这两个元素进行相互比较。 而针对这个，我们是可以从理论上进行证明，也就是任何的排序算法，只要这个排序算法会存在一个取出元素的动作，
不搜索，无问题。冗余、上下界剪枝
公众号：编程驿站 1. 搜索算法 本文和大家聊聊搜索算法，计算机解决问题的抽象流程是，先搜索，或完全搜索后得到答案，或边搜索边找答案。所以，对给定的数据集进行搜索是解决问题的前置条件。不搜索，无问题。 搜索算法无非就是线性、二分、深度、广度搜索算法。其它的搜索算法的底层逻辑也是建立这4 种之上的。如双向广度搜索、启发式搜索……均是对原生搜索算法进行了优化。 计算机是穷举思维，解决任何问题的
【矩阵论】特征值的估计(上下界和盖尔圆)
前言：为什么不直接求特征值而是去估计特征值？ 当我们遇到的不是书本上的3阶或4阶矩阵，而是高阶矩阵时(如图像中的256×256)，我们再使用特征方程 det ( λ I − A ) = 0 \det(\lambda I -A)=0 det(λI−A)=0来求特征值就非常困难。我们难以求解也没有必要逐一计算每一个精确的特征值。因此，在实际工程计算上，面对高阶矩阵，我们常常通过计算特征值的范围来
下界通配符（? super Type）
在Java中，? super Type是一个下界通配符，表示参数化类型的下限是Type。这意味着容器可以持有Type类型的任何对象或者Type的父类型对象。 使用场景 这种类型的通配符通常用于泛型方法中，允许方法接受Type的实例或其父类型的集合。这是基于PECS原则（Producer Extends, Consumer Super），即如果你需要一个提供（生产）指定类型元素的集合，使
![上下界取min/max的线段树问题：P8518 [IOI2021] 分糖果](https://img-blog.csdnimg.cn/direct/b3bf93f944a4491687c6137bb5f35f0d.png)
上下界取min/max的线段树问题：P8518 [IOI2021] 分糖果
https://www.luogu.com.cn/problem/P8518 没有要求在线，显然离线（。维护时间戳，上线段树。 好了，我们现在知道一个人的曲线变化了。怎么做呢？ 前面所有碰上下界的都是没用的！我们只需要找最后一段的时间段满足差值为 c i c_i ci即可。因为差值更大的我们显然可以最后又会规约成这种情况。 关于差值的维护，我们维护后缀min/max，然后线段树上二分即
ACM-ICPC 2018 沈阳赛区网络预赛 D A*算法 F 有上下界的网络流 G分解质因数+公式 容斥 I 模拟 K讨论
D 题意：找是否存在第k短路且判断长度是否小于等于T。 思路：A*算法裸题。 #include <bits/stdc++.h>#define INF 0x3f3f3f3fusing namespace std;const int AX = 1e5+66;const int MAXN = 1e4+66;int n , m , k;int s ,t ;int tot ;int r
从零单练网络流 第三章 有上下界的可行流
可行流无非就是把给定的一些条件转化为最大流可以完成的任务，著名的题目有SGU上的两道题P194 Reactor Cooling和P176 Flow Construction。第一题我本想依靠自己想出最大流的模型，不过最后还是看了题解。 这里简要讲一下P194 Reactor Cooling这道题的解法，这题在ACdream上也有，P1211。题意大概为给你n个点，m条边，每条边有上下界流，
泛型笔记3-下界通配符
上一节讨论了上界通配符的作用以及它的使用事项.今天将讨论下界通配符. 下界通配符 当我们需要动态地传入类对象及其超类类型的时候,由于擦除性质,编译器并不能确定所传入的对象是否是某一个对象的超类,而将它们都视作Object对象.当我们需要一个能使编译器识别这种关系的一种通配符,所以我们就有了下界通配符这一概念. 它的格式为:<? super 类名>. 它告诉编译器,你所要传入的参数类型只能是这个
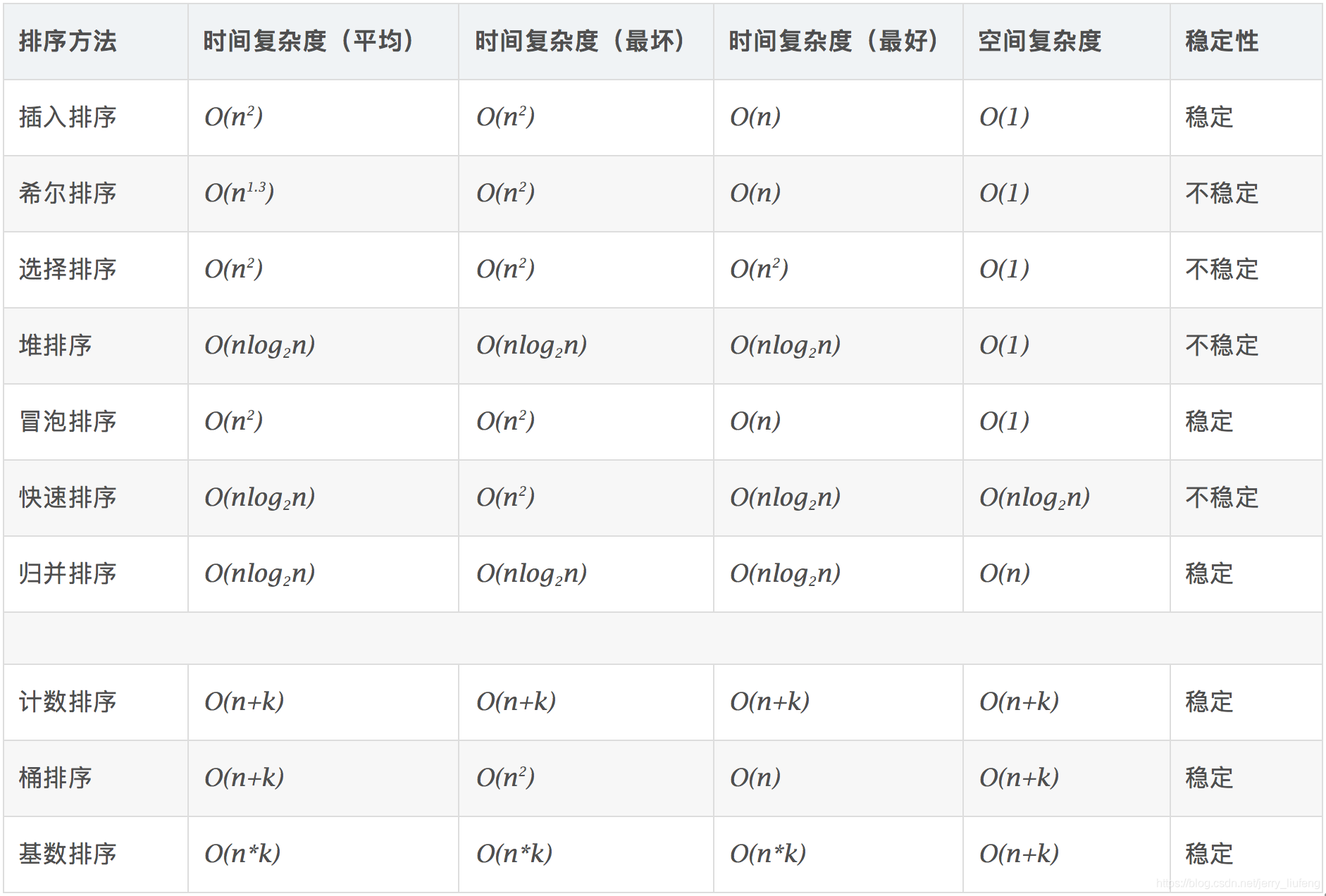
排序算法的下界和如何超越下界——python实现Thomas H.Cormen算法基础中的算法
文章目录 一、排序算法分类二、算法复杂度三、时间复杂度下界四、超越下界1.范例1——严格的约束（排序仅有两个值）2.范例2——扩展1至每个元素可以取m个连续整数中的一个 一、排序算法分类 比较类排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn)，因此也称为非线性时间比较类排序。非比较类排序：不通过比较来决定元素间的相对次序，它可以突破基于比较排序的