排序算法的下界和如何超越下界——python实现Thomas H.Cormen算法基础中的算法

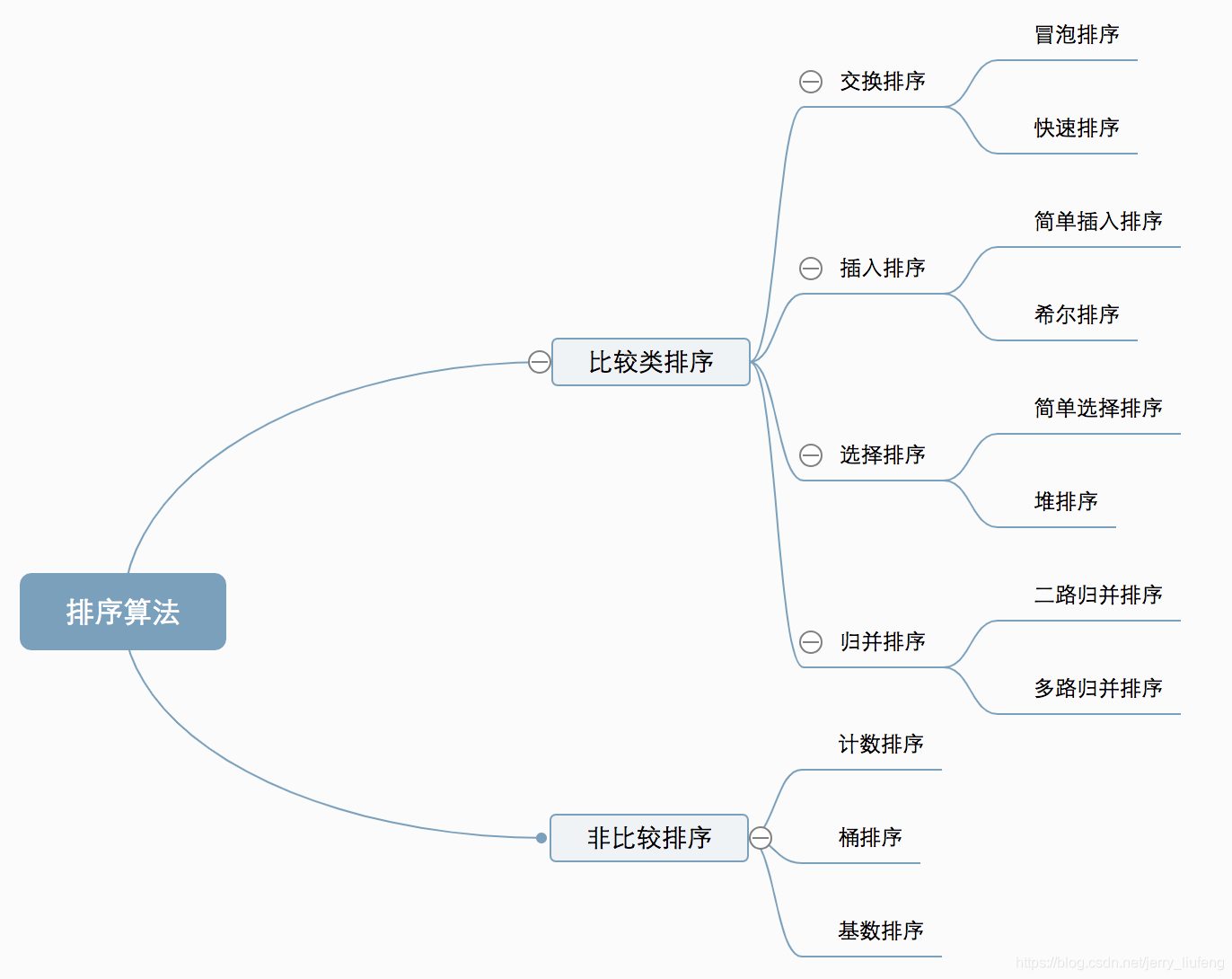
一、排序算法分类

• 比较类排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn)，因此也称为非线性时间比较类排序。
• 非比较类排序：不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。

二、算法复杂度

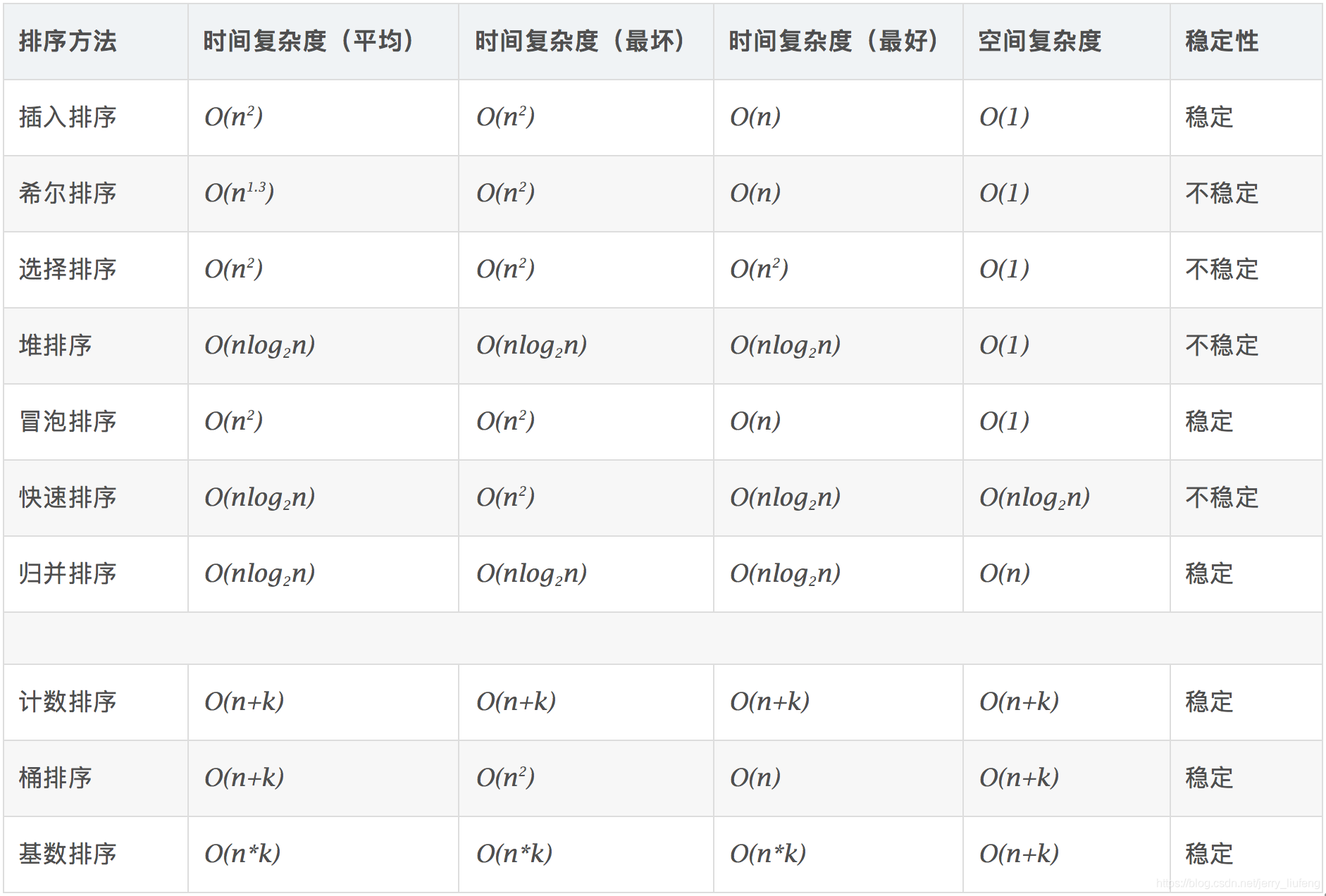
相关概念：

• 稳定：如果a原本在b的前面，而a=b，排序之后a仍然在b的前面
• 不稳定：如果a原本在b的前面，而a=b，排序之后a可能会出现在b的后面
• 时间复杂度：对排序数据的总的操作次数。反映当n发生变化的时候，操作次数呈现什么规律
• 空间复杂度：算法在计算机中执行时所需要存储空间的度量，是数据规模n的函数

三、时间复杂度下界

观察插入排序、希尔排序、选择排序、堆排序、冒泡排序、快速排序、归并排序的时间复杂度，在没有特殊规则的时候时间复杂度为$O(nlogn)$就是最优的排序算法了

也就是说通用排序算法的时间复杂度下界就是$O(nlogn)$

如果限定一些规则，是可以打破这个下界的。

下面说一下尽在O(n)时间内就能实现对数组排序的算法、

四、超越下界

问题：基于什么样的规则才能突破排序的下界呢？

基础思想:我们需要分析一下排序消耗的时间。排序需要遍历，比较，交换。能否省略其中的一些步骤呢？这就是要定义的规则，通过规则减少排序步骤。

1.范例1——严格的约束（排序仅有两个值）

一组待排序的元素仅有1和2，没有其它值，对这组数进行排序。

输入$A_0，A_1,A_2,A_3......A_{n-1}$，Ai为1或者2

排序步骤

1. 令k=0
2. 令i从0到n-1依次取值，如果A[i]=1,k自增1
3. 令i从0到k-1依次取值，将A[i]赋值为1
4. 令i从k到n-1依次取值，将A[i]赋值为2

这样我们完成了排序，花费的时间为O(n)
之前我们所说的算法都是通过比较元素对来确定顺序，那种排序叫做比较排序。凡是比较排序，通用下界为O(nlogn)

# 非常简单的实现，每一步都对应于上述四个步骤
A = [1,2,1,1,1,2,1,2,1,2,1]
print('排序前：',A)
n = len(A)
k = 0
for i in range(0,n):if A[i]==1:k+=1for i in range(0,k):A[i] = 1for i in range(k,n):A[i] = 2print('排序后：',A)

结果：

排序前： [1, 2, 1, 1, 1, 2, 1, 2, 1, 2, 1]
排序后： [1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2]

2.范例2——扩展1至每个元素可以取m个连续整数中的一个

只要每个元素在m个连续整数值中取值，算法都是通用的

该算法的实现需要三个基本方法:

COUNT-KEY-EQUAL(A,n,m)

输入:A 一个数组，n 数组A中的元素个数m数组A中元素的取值范围
输出:一个数组$equal[0......m]$,是$equal[j]$等于数组A中元素值为j的元素个数

1. 创建一个新数组$equal[0......m]$
2. 令$equal$数组每个元素都为0
3. i从0到n-1依次取值，每次将$equal[A[i]]$的值自增1
4. 返回$equal$

COUNT-KEY-LESS(equal,m)

输入值COUNT-KEY-EQUAL方法对应的值$equal，m$
输出一个数组$less[0......m],less[j]=equal[0]+equal[1]+......+equal[j-1]$

1. 创建一个新数组$less[0...m]$
2. 令$less[0]=0$
3. j从1取到m,$less[j]=less[j-1]+equal[j-1]$(这是普通的迭代算法)
4. 返回$less$

REARRANGE(A,less,n,m)

输入COUNT-KEY-EQUAL COUNT-KEY-LESS方法对应的$A，less,n,m$
输出数组B，B中包含A中所有元素，并且已经排好序

1. 创建新数组$B[0...n-1],next[0.....m]$
2. j从0到m依次取值
   令$next[j]=less[j]+1$
3. 令i从0到n-1依次取值
   $key=A[i];index=next[key],B[index]=A[i],next[key]++$
4. 返回数组B

## 代码实现：
import numpy as np
def CountKeyEqual(A,n,m):equal = np.zeros(m+1)for i in range(0,n):equal[A[i]]+=1return equal
def CountKeyLess(equal,m):less = np.ones(m+1)less[0] = 0 for j in range(1,m+1):less[j] = less[j-1]+equal[j-1]return less
def Rearrange(A,less,n,m):B = np.ones(n)next_ = np.ones(m+1)for j in range(m+1):next_[j] = less[j]+1for i in range(n):key = A[i]index = next_[key]B[int(index)-1] = A[i] # 注意这里与文本序数有些把不同在于B的索引大小应该与A的一致next_[key]+=1return B
if __name__=='__main__':A = [4,1,5,0,1,6,5,1,5,3]n = len(A)m = 6print('排序前：',A)equal = CountKeyEqual(A,n,m)less = CountKeyLess(equal,m)B = Rearrange(A,less,n,m)B = B.astype(np.int).tolist()print('排序后：',B)

结果：

排序前： [4, 1, 5, 0, 1, 6, 5, 1, 5, 3]
排序后： [0, 1, 1, 1, 3, 4, 5, 5, 5, 6]