本文主要是介绍【概率论与数理统计】统计学假设检验的原假设H0、备择假设H1怎么确定?,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
可以参考我的另一篇博文:
【假设检验】单侧检验时,对拒绝域在左侧还是右侧的理解
统计学假设检验的原假设H0、备择假设H1怎么确定?
回答1
简单来说,就是反正法。
双侧检验
某机床厂加工一种零件,根据经验知道,该厂加工零件的椭圆度近似服从正态分布,其总体均值为m0=0.081mm,总体标准差为s= 0.025 。今换一种新机床进行加工,抽取n=200个零件进行检验,得到的椭圆度为0.076mm。试问新机床加工零件的椭圆度的均值与以前有无显著差异?
问: 有无显著变化
验证: 没有显著变化
原假设: 有显著变化,等号放在原假设
单侧检验
根据过去大量资料,某厂生产的灯泡的使用寿命服从正态分布N~(1020,1002)。现从最近生产的一批产品中随机抽取16只,测得样本平均寿命为1080小时。试在0.05的显著性水平下判断这批产品的使用寿命是否有显著提高。
问:有无显著提高
验证:有显著提高
原假设:没有显著提高,等号放在原假设
回答2
这个问题是每个学到这一部分的学生都会感到困惑的问题。
设原假设为H0,备择假设为H1,置信水平为95%
H0与H1从逻辑上说本来是二择一的,非此即彼,对于原假设检验的结果逻辑上说只有两个,要么对的,要么错的,如果H0是对的,那么H1就必定错了,如果H0错了,那么H1就必定是对的,如此说来,随便把哪一个作为原假设应该都是一样的结果。但事实上,选择哪个作为原假设是有差别的,那么问题出在哪儿呢?
其实问题出在假设检验的结果上,统计中用的假设检验的方法,对于原假设得到的结论不是“对”与“错”两个结果,而是“拒绝”与“接受”,两者有什么差别吗?
一定要注意在做假设检验的时候,都要设定一个置信水平,当我们“拒绝”原假设的时候,实际上我们只是说“我们有95%的把握”说原假设错了,也就是说,它还是有可能是对的,换句话说,我们不能逻辑上否定原假设!
再来说“接受”原假设,这个“接受”两个字,害苦了几乎所有的学生,其实准确的说法应该是“不能拒绝”原假设,比如说原假设H0是:期望=2,如果“拒绝”H0, 那么意思是我们有95%的把握说H0是错的,但是当我们所谓“接受”H0的时候,我们并不是有95%的把握肯定期望就等于2,其实我们一点把握都没有,我们只是利用现有样本数据不能否定它是2而已,它完全可能是2.1,2.11,1.95…等等等等。
综上我们注意到两点:一是我们的“拒绝”和“接受”原假设,不是逻辑上的对与错;二是我们“拒绝”原假设和“接受”原假设是完全不对等的,当我们拒绝原假设的时候,我们有95%的把握;但是当我们接受原假设的时候,我们一点把握都没有。由此可知当我们选择原假设的时候,应该选择我们有比较大的把握否定它的一面。
关于这个问题更精细的讨论要牵涉到置信区间的长度问题,需要画图,这里比较难弄,自己找资料看去吧。
//你想证实的结论应该设置为备择假设而不是原假设,因为原假设只能被证伪,不能被证实
回答3
是这样的,假设检验是倾向于保护原假设的。
比如说要推广一种新药,如果原假设是该药可靠,那只有很不可靠的时候才会拒绝。但若原假设是该药不可靠,只有很可靠的时候才会拒绝。在这个具体问题中,推广新药必须要很可靠才行,所以一般会把原假设定为该药不可靠。再说仔细一些,一般取置信区间为0.05,也就是说只有当原假设前提下5%的小概率事件发生时,才会拒绝原假设。具体的判别方法你再复习一下关于置信水平的知识,会有更深的理解。希望能帮到你
回答4
我们常把没有充分理由不能轻易否定的命题作为原假设H0,而常把没有把握不能轻易肯定的命题作为备择假设H1.
比如:某装置的平均工作温度据制造厂家称低于190,今从一个由16台装置构成的随机样本测得工作温度的平均值和标准差分别为195和8,根据这些数据能否支持厂家结论?设α=0.05,并假设工作温度近似服从正态分布。
按照题意来选择原假设与备择假设。
如果我是生产厂商,我肯定希望选择对自己有利的假设,而u<190可以保证我的产品的样本统计值即使超出这个温度一定范围内仍然可以被通过,这实际上是对本产品放松了检验要求。
如果我是经销商我希望得到更好质量的产品,我希望严格检验要求,选择u>190为原假设,这样的话即使样本统计值在小于190的小范围内仍然会通过经销商的原假设,换句话说对于生产厂商来说在小于190的小范围内的产品就损失了检验价值(即使这些产品是毫无疑问合格的),而经销商如果要得到温度小于190的备择假设,就需要统计值不仅要小于190,而且要尽量远离190,即发生显著性水平为0.05的事件,这对于产品要求来说是严格的.
举例:扇贝抽样案例

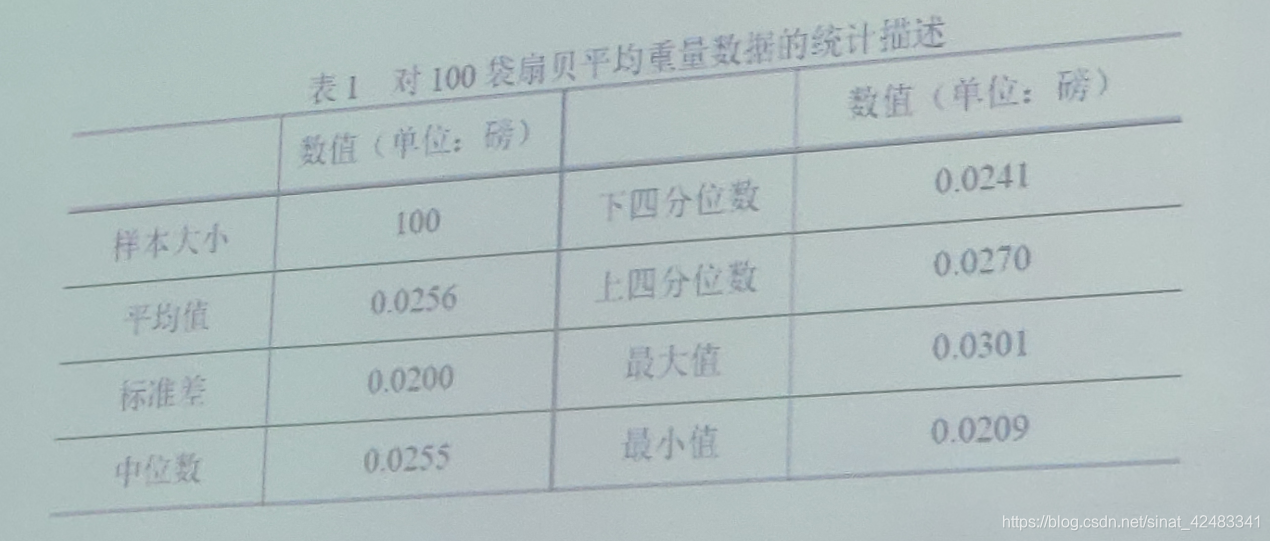
如果我们希望让扇贝的质量符合标准,应该原假设为平均质量μ>=0.0278,这样只有在很不可靠的时候才能拒绝原假设。

这篇关于【概率论与数理统计】统计学假设检验的原假设H0、备择假设H1怎么确定?的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









