本文主要是介绍Efficient Off-Policy Meta-Reinforcement Learning via Probabilistic Context Variables,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

Abstract
\quad 深度RL算法需要大量经验才能学习单个任务。原则上,元强化学习(meta-RL)算法使智能体能够从少量经验中学习新技能,但一些主要挑战阻碍了它们的实用性。当前的方法严重依赖于同策经验,从而限制了其采样效率。在适应新任务时,也缺乏推断任务不确定性的机制,从而限制了它们在稀疏奖励问题中的有效性。在本文中,我们通过开发一种异策元RL算法来解决这些挑战,该算法可以分离任务推断和控制。在我们的方法中,我们对隐任务变量执行在线概率滤波,以从少量经验中推断出如何解决新任务。这种概率解释可以进行后验采样,以进行结构化且有效的探索。我们演示了如何将这些任务变量与异策RL算法集成在一起,以实现高效元训练与适应。在几个元RL基准测试中,我们的方法在样本效率和渐近性能方面都比以前的算法好20-100倍。

学习方法擅长于制造agents that are specialists——擅长于一项特定的任务。
在现实中,我们希望我们的 agents to be generalists ——擅长各种行为,能够利用这个世界的结构更快地学习新任务。
例如,冲浪、滑板和滑雪都需要在滑板移动时保持身体平衡。
如果一个agent已经很擅长这些运动中的一项,我们希望他能更快地学会另一项。
我们可能知道 the shared structure 存在,但不知道它是什么,也不知道如何在我们的模型中包含它。
我们采用 learning-based approach 从数据中学习这个结构 。
整体思路
\quad 元训练包括两件事:
- 学习将情境概括为变量z,
- 学习根据给定z采取最佳行动的策略。

\quad 文章提出了一种 off-policy meta RL 算法。
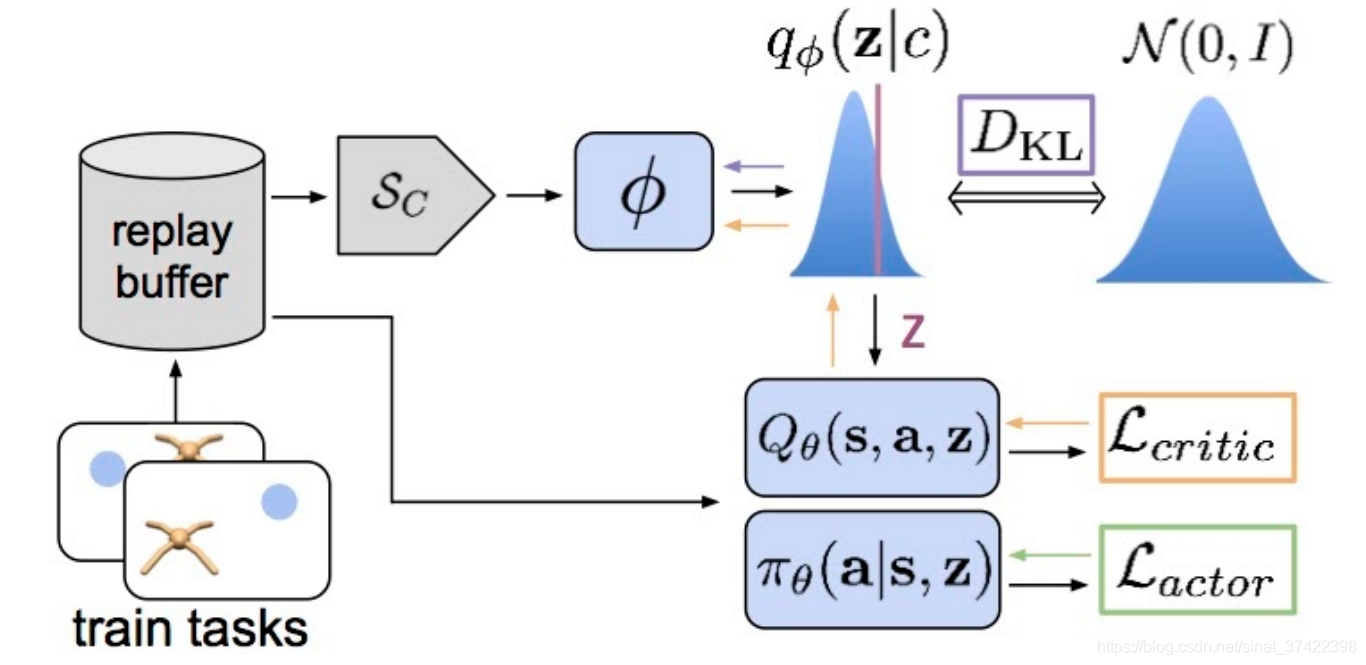
- The latent task variable z 通过参数为 ϕ \phi ϕ 神经网络 从 latent context 中推理出来
- actor 和 Critic 将 z 作为输入,以便根据当前的任务采取行动。
- 注意,从 reply buffer 中抽取了2个batch 数据— 用于推断z的上下文,用于训练 actor 和 Critic 。

\quad 如果只是学 the latent task variables z ,那就体现不出探索了,所以用 a belief distribution 代替它;belief 代表了 我们对推理出的当前任务 z 的确信度(belief就是DKL),利用它来在之后与环境交互时的 a temporally-extended manner 中进行探索。
\quad 在 adaptation阶段,我们采样一个 z,根据这个z选择动作,然后获得样本之后再更新belief。
This belief represents our uncertainty about the current task, and we can make use of it to explore in a temporally-extended manner via posterior sampling.
During adaptation, we iteratively sample a z, act according to it for a trajectory, and subsequently update our belief given the new evidence.
3 任务定义


4. Probabilistic Latent Context
4.1 Modeling and Learning Latent Contexts
\quad 目标 :生成 latent context Z Z Z
\quad 利用 摊销变分推断方法 (amortized variational inference approach)。训练一个 推断网络 q ϕ ( z ∣ c ) q_\phi(z|c) qϕ(z∣c),其中 ϕ \phi ϕ 是参数, c c c 是历史经验 c 1 : N τ c^\tau_{1:N} c1:Nτ 的简单表示。用 q ϕ ( z ∣ c ) q_\phi(z|c) qϕ(z∣c) 来近似估计 后验概率 p ( z ∣ c ) p(z|c) p(z∣c) 。
\quad 生成阶段文中提到两种方法:
- 基于模型的方法:通过学习一个reward的预测模型重建一个MDP,来优化 q ϕ ( z ∣ c ) q_\phi(z|c) qϕ(z∣c)
- model-free 的方法:
a. 建模 state-action 价值函数
b. 通过任务分布中的 policy 来最大化回报
假设我们的目标为对数似然函数,则变分下界为:

其中 p ( z ) p(z) p(z)是 Z Z Z上的高斯先验分布。
\quad 在 元训练期间 我们优化了 q ϕ q_\phi qϕ 的参数,但是在元测试期间,我们仅从收集的经验中推断 新任务的 隐上下文(latent context)。
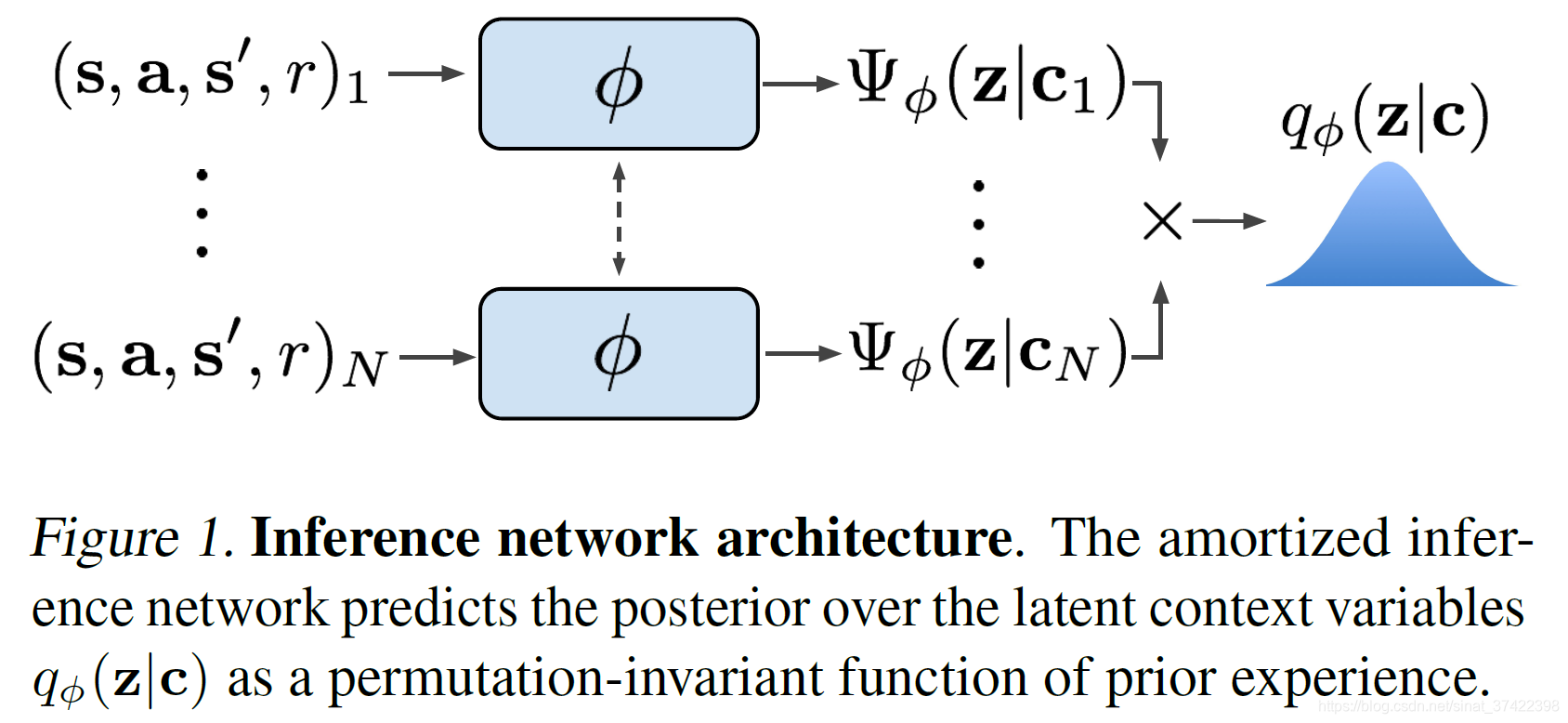
\quad 如何设计 推断网络 q ϕ ( z ∣ c ) q_\phi(z|c) qϕ(z∣c) 的结构?
\quad 我们希望推断网络能够提取有效的任务信息,剔除无关的信息。也就是需要能够推断出任务是什么( z z z 表示新任务是什么)。要做到这一点,只要有 transitions { s i , a i , s i ′ , r i } \{s_i,a_i,s'_i,r_i\} {si,ai,si′,ri} 的就行,需要注意的是我们不需要考虑这些 transitions 的顺序,基于这一点,我们选择一个 permutation invariant representation(置换不变性)的表示方式,将 q ϕ ( z ∣ c 1 : N ) q_\phi(z|c_{1:N}) qϕ(z∣c1:N) 建模为 独立因子的乘积:
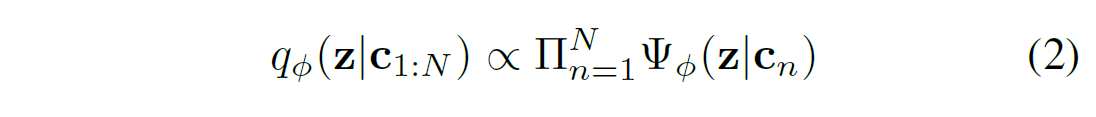
\quad 其中 Ψ ϕ ( z ∣ c n ) \Psi_\phi(z|c_n) Ψϕ(z∣cn)使用 高斯因子 (为了方便),which result in a Gaussian
posterior:
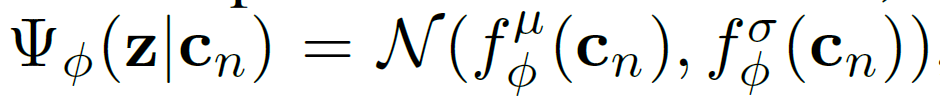
\quad 其中, f ϕ f_\phi fϕ 是 参数为 ϕ \phi ϕ 的神经网络,输出为 均值 μ \mu μ 和 方差 δ \delta δ,以此来形成一个高斯分布。如下图1所示:
4.2. Posterior Sampling and Exploration via Latent Contexts
\quad 将 Latent Context 建模为概率模型之后,在 meta-test 阶段就可以进行采样(探索)。在经典RL中,从 MDP 的 先验分布 开始(prior distribution),然后根据收集的历史经验计算 后验分布 (posterior distribution),根据后验分布进行采样;在执行 action 阶段,选取采样中的最优策略,将之视为最有效的探索。
\quad 我们的方法 PEARL 直接计算 Latent contexts 的一个后验分布,对应于生成阶段的三个方法:
- 对重构的 MDP 进行优化,就 encode the MDP itself
- 对policy进行优化,则对 optimal behaviors 进行编码
- 对critic进行优化,则对 value function 进行编码
\quad 在 meta-test 阶段,我们先从 先验分布 中采样 z z z 并根据每个 z z z 执行一个回合,从而可以在时间维度上扩展,以多样化的方式进行探索(对比之前的时间无序)。然后,用新收集到的经验更新后验分布,随着 belief 变窄(置信区间变窄),动作也越来越优化。
5. Off-Policy Meta-Reinforcement Learning
\quad 上文讲的是 on-policy 方法,接下来讲 如何转换为 off-policy 方法,这样在 meta-training 和 fast adaptation 阶段都会提高数据利用率(不用太多数据啦)。
\quad 之前的 meta-training 中使用了 on-policy 方法,这是因为 modern meta-learning
基于一个假设: the distribution of data used for adaptation will match across meta-training and meta-test. 需要 元训练 和 元测试 的数据是同策的。(注意,元测试是在新任务上进行测试,所以元测试的数据是同策略的;但是元训练阶段不一定)

\quad 我们使用 probabilistic context 的方法 来设计 off-policy meta-RL method 的 主要观点是 : 用于训练 encoder 的数据分布 不必与 训练 policy 的数据分布相同。policy 可以将 context z z z 视为 state 的一部分,探索过程中的随机性由 encoder q ( z ∣ c ) q(z|c) q(z∣c) 的不确定性提供。
\quad 定义 采样器 S c S_c Sc 来采样 context batches 来训练 encoder。
\quad 从整个replay buffer采样会导致与 同策略测试数据 的分布 太不匹配。由于不必严格同策。并且作者发现 an in-between strategy of sampling from a replay buffer of recently collected data(replay buffer 中最近收集的数据 中采样 中间的策略)能够保证较高的同策性。训练过程如图2所示。


5.1. Implementation
\quad 用SAC。
\quad 用 reparameterization trick 来优化 推断网络 q ϕ ( z ∣ c ) q_\phi(z|c) qϕ(z∣c)、actor π θ ( a ∣ s , z ) \pi_\theta(a|s,z) πθ(a∣s,z)、critic Q θ ( s , a , z ) Q_\theta(s,a,z) Qθ(s,a,z) 的参数,通过采样的 z z z 为 q ϕ ( z ∣ c ) q_\phi(z|c) qϕ(z∣c) 计算梯度。
\quad Critic loss:
\quad 作者发现 训练 encoder q ϕ ( z ∣ c ) q_\phi(z|c) qϕ(z∣c) 来优化 state-action value function 效果更好,所以在Critic loss部分更新 q ϕ ( z ∣ c ) q_\phi(z|c) qϕ(z∣c) 的参数 ϕ \phi ϕ :
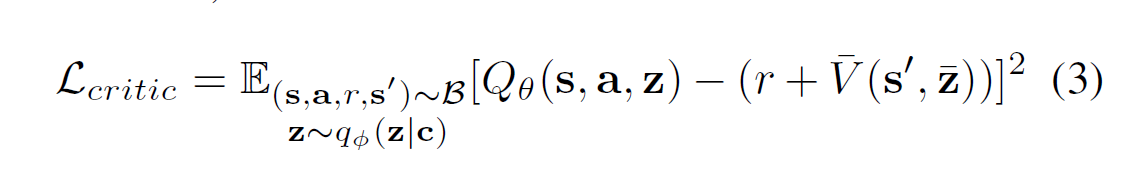
其中, V ˉ \bar{V} Vˉ 是 target network ; z ˉ \bar{z} zˉ 表示 没有对它计算梯度。
\quad Actor loss:
\quad 与 SAC 的计算方式一样,只不多多了 z ˉ \bar{z} zˉ 作为 a policy input:
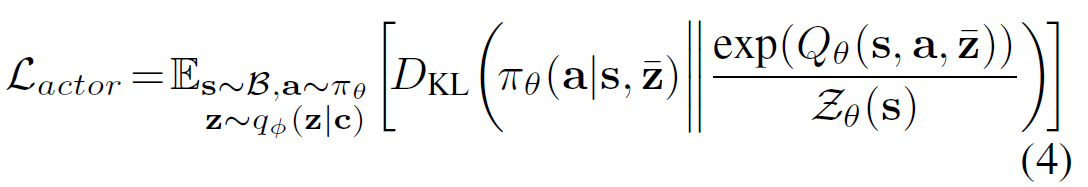
注意:在推理出 z z z 阶段 q ϕ ( z ∣ c ) q_\phi(z|c) qϕ(z∣c) 中的 c c c 与 构建 Critic loss 的 c c c 不同。
总结:
1)First off-policy meta-RL algorithm
2)在样本效率和渐近性能方面都比以前的算法好20-100倍
20-100X improved sample efficiency on the domains tested, often substantially better final returns
3)Probabilistic belief over the task enables posterior sampling for efficient exploration
代码:
Note 5/22/20: The ant-goal experiment is currently not reproduced correctly. We are aware of the problem and are looking into it. We do not anticipate pushing a fix before the Neurips 2020 deadline.(收到反映说没能重现,作者说她在解决)
katerakelly/oyster: Implementation of Efficient Off-policy Meta-learning via Probabilistic Context Variables (PEARL)
作者信息:
Kate Rakelly http://people.eecs.berkeley.edu/~rakelly/
这篇关于Efficient Off-Policy Meta-Reinforcement Learning via Probabilistic Context Variables的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



![[论文笔记]QLoRA: Efficient Finetuning of Quantized LLMs](https://img-blog.csdnimg.cn/img_convert/e75c9a4137c39630cd34c5ebe3fe8196.png)




