本文主要是介绍基于图搜索的自动驾驶规划算法 - BFS,Dijstra,A*,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本文将讲解BFS,Dijstra,A*,动态规划的算法原理,不正之处望读者指正,希望有兴趣的读者能在评论区提出一些这些算法的面试考点,共同学习,一起进步
0 图论基础
图有三种:无向图、有向图、带权重的图
无向图

有向图

带权重的图

1 BFS
广度优先搜索算法
利用队列queue数据结构实现:先进先出
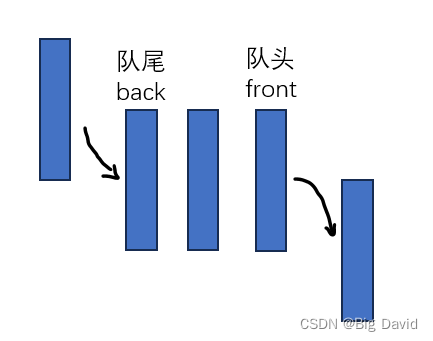
算法流程(伪代码):
BFS(G, start, goal):let Q be queue;Q.push(start);mark start as visited;while (!Q.empty()){v = Q.front();Q.pop();if (v is the goal) return v;for all neighbours n of v in GQ.push(n);n->parent = v;mark n as visited;}
BFS总结:
(1)相同探索所有的方向
(2)如果所有边权重为1,那么用BFS搜索出来的路径是cost最优的
(3)在不同的场景中,不能保证所有的边权重为1,对于这些场景,BFS受限
2 Dijstra
核心思想:
(1)相比BFS,Dijstra维护一个新变量g(n),g(n)表示从起始节点到当前节点的累积成本
(2)从openset(Min-priority queue)中访问累积成本g最低的节点
算法流程(伪代码):
Dijstra(G, start, goal):let open_list be priority_queue;open_list.push(start, 0);g[start] = 0;while (!open_list.empty()){current = open_list.pop();mark current as visited;if (current is the goal) return current;for (all unvisited neightbours next of current in G){next_cost = g[current] + cost(current, next);if (next is not in open_list)open_list.push(next, next_cost);else {if (g[next] > next_cost)g[next] = next_cost;}}}
优点:
(1)Dijstra算法能找到从起始节点到图上所有其他节点的最短路径
(2)Dijstra算法满足最优性
缺点:每次都会从open_list寻找代价最少的节点,但是并不知道终点在哪,如果用这个算法做图中特定两个点的最短路径,是比较低效的
3 A*算法
A*算法手撕版本见手撕A算法(详解A算法)
核心思想:
(1)相比Dijstra,A*将目标点的成本估计为启发式信息以提高效率
(2)启发式函数h(n):表示从节点n到目标的估计成本
(3)评估每个节点的成本函数:f(n)=g(n)+h(n)
(4)从open_list选择f-score最低的节点,而不是Dijstra算法中的g-score
算法流程(伪代码):
Astar(G, start, goal):let open_list be priority_queue;g[start] = 0;f[start] = g[start] + h[start];open_list.push(start, f[start]);while (!open_list.empty()){current = open_list.pop();mark current as visited;if (current is the goal) return current;for all unvisited neighbours next of current in Gnext_cost = g[current] + cost(current, next);if (next is not in open_list)open_list.push(next, next_cost + h[next]);else{if (g[next] > next_cost) {g[next] = next_cost;f[next] = next_cost + h[next];}}}
启发式函数设计
在路径搜索过程中,没有唯一启发函数设计原则,需要根据特定的任务来设计,如果最优性和距离相关,则可以计算节点之间的直线距离来估计
三种常用的距离:
起点: ( p 1 , p 2 ) (p_1, p_2) (p1,p2) 终点: ( q 1 , q 2 ) (q_1, q_2) (q1,q2)
(1)Euclidian distance
d ( p , q ) = ( q 1 − p 1 ) 2 + ( q 2 − p 2 ) 2 d(p,q)=\sqrt{(q_1-p_1)^2+(q_2-p_2)^2} d(p,q)=(q1−p1)2+(q2−p2)2
(2)Manhattan distance
d ( p , q ) = ∣ q 1 − p 1 ∣ + ∣ q 2 − p 2 ∣ d(p,q)=|q_1 - p_1|+|q_2 - p_2| d(p,q)=∣q1−p1∣+∣q2−p2∣
(3)Great circle distance

△ σ = a r c c o s ( s i n ϕ 1 s i n ϕ 2 + c o s ϕ 1 c o s ϕ 2 c o s ( △ λ ) ) \bigtriangleup \sigma =arccos(sin\phi _1sin\phi_2+cos\phi_1cos\phi_2cos(\bigtriangleup\lambda )) △σ=arccos(sinϕ1sinϕ2+cosϕ1cosϕ2cos(△λ))
d = r △ σ d = r\bigtriangleup \sigma d=r△σ
最优性
启发式函数 h ( n ) < c o s t ( n , g o a l ) h(n)<cost(n,goal) h(n)<cost(n,goal)
只要启发式函数提供了小于实际成本的估计,A*将始终找到最优路径,并且通常比Dijstra快
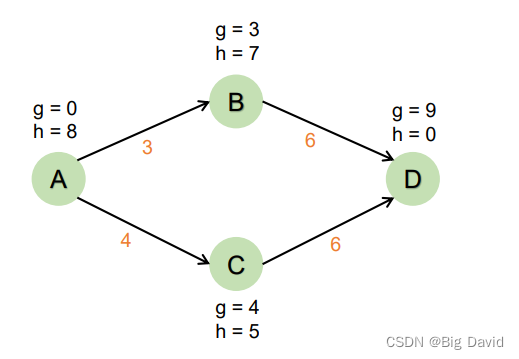
实际上A->B->D是最短路径
因为B的启发式函数高估了对目标的成本
这种高估导致搜索算法相信节点C总成本低于节点B,使得节点C在节点B之前访问,导致结果不是最优路径
在gridmap中如何设计启发式函数

使用8连接,曼哈顿距离启发式高估了成本
欧几里得距离总是可以接受
A*算法的精度和效率

(1) h ( n ) = 0 h(n)=0 h(n)=0:A退化为Dijstra
(2) h ( n ) < c o s t ( n , g o a l ) h(n)<cost(n,goal) h(n)<cost(n,goal):A满足最优性,效率比Dijstra更高
(3) h ( n ) = c o s t ( n , g o a l ) h(n)=cost(n,goal) h(n)=cost(n,goal):A满足最优性,并且有最高的效率
(4) h ( n ) > c o s t ( n , g o a l ) h(n)>cost(n,goal) h(n)>cost(n,goal):A不满足最优性,高估实际成本
BFS、Dijstra、A*总结:
| BFS | Dijstra | A* |
|---|---|---|
| (1)BFS算法会朝着周围等价扩展 | (1)相比BFS,Dijstra倾向于累积成本最小化,不是平等地搜索所有可能的路径,能在加权图中满足最优性 | (1)A*是Dijstra的修改,添加了启发式函数h(n)提高搜索效率 |
| (2)如果每条边权重为1,BFS搜索出来的path也是最优解 | (2)如果每条边权重为1,BFS=Dijstra | (3)启发式函数的设计会影响效率和准确性 |
搜索算法可视化参考:http://qiao.github.io/PathFinding.js/visual/
4 动态规划
- 定义:
一种计算机编程方式,首先把算法问题分解为子问题,求解这些子问题,并把这些结果保存下来,然后优化子问题找到整个问题的最优解
- 动态规划的性质:
(1)最优子结构
面对一个大问题可以分解为一系列子问题。如果能找到每个小问题的最优解,并且能够把小问题拼成大的问题。这种问题就叫最优子结构
(2)重复的子问题
动态规划不会重新计算重复的子问题,会事先保存结果
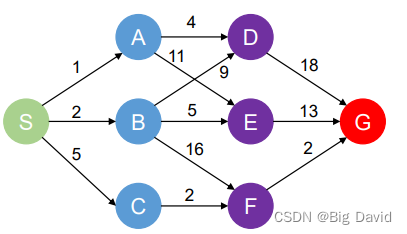
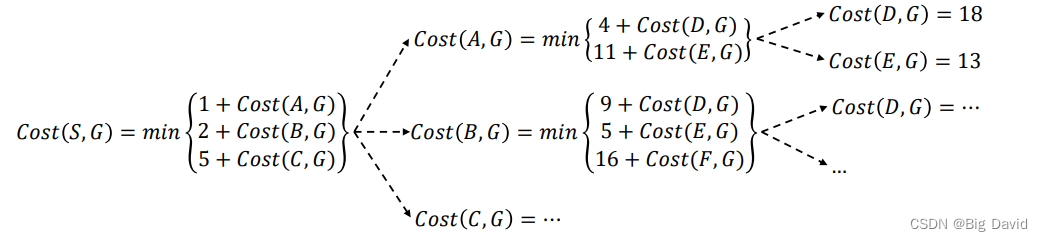
3. 计算方法
(1)前向法
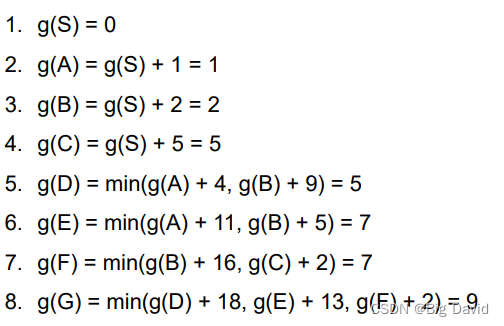
(2)逆向法
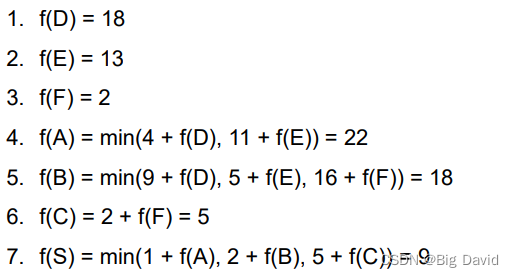
这篇关于基于图搜索的自动驾驶规划算法 - BFS,Dijstra,A*的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









