GAMES101-LAB1

本文主要是介绍GAMES101-LAB1，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

一、问题简述

• 接下来的三次作业，将模拟一个基于CPU的光栅化渲染器的简化版本
• 本次作业的任务是实现一个旋转矩阵和一个透视投影矩阵
  • 给定三维下三个点v0(2.0, 0.0,−2.0), v1(0.0, 2.0,−2.0), v2(−2.0, 0.0,−2.0), 将这三个点的坐标变换为屏幕坐标并在屏幕上绘制出对应的线框三角形
  • 在代码框架中，已经提供了draw_triangle 函数，只需要去构建变换矩阵即可
• 需要在main.cpp 中修改的函数
  • get_model_matrix(float rotation_angle): 逐个元素地构建模型变换矩阵并返回该矩阵。在此函数中，只需要实现三维中绕z轴旋转的变换矩阵，而不用处理平移与缩放
  • get_projection_matrix(float eye_fov, float aspect_ratio, float zNear, float zFar): 使用给定的参数逐个元素地构建透视投影矩阵并返回该矩阵
  • [Optional] main(): 自行补充你所需的其他操作

二、框架准备

• 首先需要安装OpenCV, 我选择的是OpenCV–3.4.10
  • 安装过程可以参考这篇博文: https://blog.csdn.net/public669/article/details/99044895
• rasterizer.hpp 和main.cpp。其中rasterizer.hpp 文件作用是生成渲染器
  界面与绘制
  • 可以参考我的GitHub，已添加了部分代码注释
  • https://github.com/luhexin/GAMES101-LAB/tree/main/Assignment1

三、作业参考

3.1 模型矩阵

• 题目要求围绕z轴进行旋转，注意弧度制与角度制之间的转换

3.1 参考代码

Eigen::Matrix4f get_model_matrix(float rotation_angle)
{Eigen::Matrix4f model = Eigen::Matrix4f::Identity();// TODO: Implement this function// Create the model matrix for rotating the triangle around the Z axis.// Then return it.Eigen::Matrix4f rotate;float radian_angle = rotation_angle / 180 * MY_PI; rotate << std::cos(radian_angle), -std::sin(radian_angle), 0, 0, std::sin(radian_angle), std::cos(radian_angle), 0, 0,0, 0, 1, 0,0, 0, 0, 1;model = model * rotate;return model;
}

3.2 投影矩阵

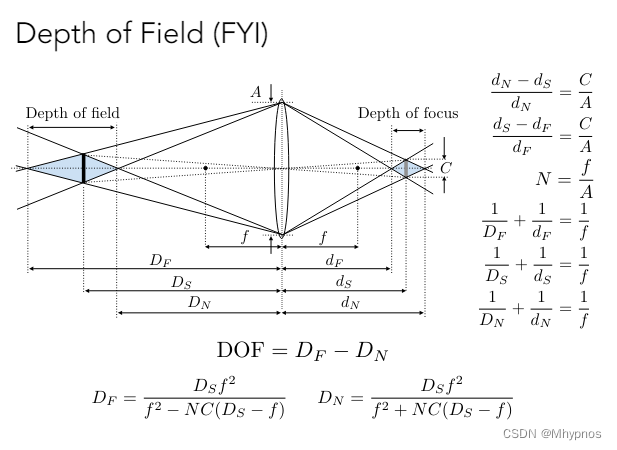
• 如何做透视投影?
  1. 压扁操作(透视投影)，将锥体压为立方体
     • 近平面点不变
     • 远平面中心点不变，其余点向中心挤压
  2. 正交投影
     • 平移、缩放为正交矩形

3.2.1 压扁操作(透视投影)

• 近平面和远平面上点的z坐标不变，但是模型其他面上的z可能会发生改变
• 根据相似三角形(x,y,z,1) => (nx, ny, unknown, z);

  • 对于任意一个点，要求有矩阵M满足: M · (x, y, z, 1)^T = (nx, ny, unknown, z)^T;

  • n是近平面距离相机的距离
    

    • 由于x,y,z时变量，而矩阵M为常量矩阵，因此可以推出如上矩阵，第三行仍未知

• 近平面上的点(离镜头距离为n)不发生变化
• 矩阵的第三行乘以向量应该得到的是n²
  • n是一个常数，所以变量x、y对应的系数为0，所以第三行是(0, 0, A, B)，AB不确定

• 考虑远平面，远平面中心点(0, 0, f)不变
  • f是远平面距离镜头的距离

---

• 联立上述方程，得到将视锥体压扁成立方体的变换矩阵
  • n：近平面与相机距离；f: 远平面与相机距离
    $$\left(\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& n+f& -nf\\ 0& 0& 1& 0\end{array}\right)$$

---

3.2.2 正交投影

• 先平移、再缩放
  • 这里n t f b r l是矩形各个面，距离相机(坐标原点)的距离
• 将x, y, z的范围均投射到[-1, 1]，因此缩放2/…

3.2.3 参考代码

Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,float zNear, float zFar)
{Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();// TODO: Implement this function// Create the projection matrix for the given parameters.// Then return it.Eigen::Matrix4f persp_matrix;//透视矩阵 Eigen::Matrix4f translate_matrix;//移动矩阵Eigen::Matrix4f scale_matirx;//缩放矩阵persp_matrix << zNear, 0, 0, 0,0, zNear, 0, 0,0, 0, zNear + zFar, -zNear * zFar,0, 0, 1, 0;float halfAngle = eye_fov / 2 / 180 * MY_PI;float height = -2 * std::tan(halfAngle) * zNear;//没有负号则三角形上下颠倒float width = height * aspect_ratio;translate_matrix << 1, 0, 0, 0,0, 1, 0, 0, 0, 0, 1, -(zNear + zFar) / 2,0, 0, 0, 1;scale_matirx << 2 / width, 0, 0, 0,0, 2 / height, 0, 0,0, 0, 2 / (zNear - zFar), 0,0, 0, 0, 1;projection = scale_matirx * translate_matrix * persp_matrix;return projection;
}

---

四、附件

作业1压缩包

这篇关于GAMES101-LAB1的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---