Games101 光栅化笔记, 作业二

本文主要是介绍Games101 光栅化笔记, 作业二，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

光栅化笔记

1、屏幕、像素、屏幕空间：
（1）屏幕：
1、像素的二维数组
2、分辨率：数组的规模
3、典型的光栅成像设备
（2）像素的抽象理解：
1、内部颜色不会变化的小方块
2、RGB三者的颜色混合
（3）对光栅化的理解：对像素进行着色

（4）屏幕空间（在闫老师课上的规定）：
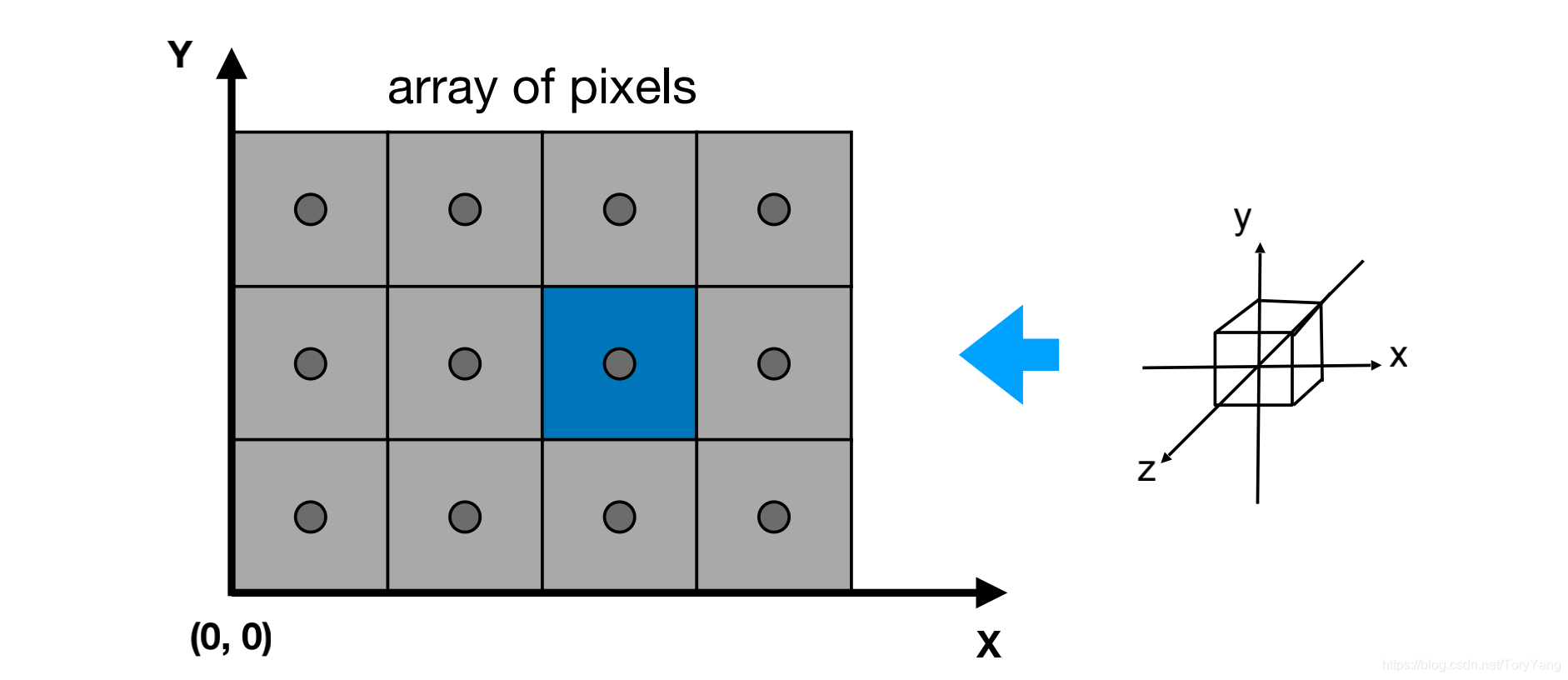
1、屏幕的左下角是原点
2、x和y坐标都取整数，下图中蓝色像素坐标为(2,1)
3、像素的索引范围是（0，0）-> （width-1，height-1）
4、(x,y)为像素坐标，则像素中心坐标为(x+0.5,y+0.5)
5、屏幕覆盖范围从（0，0） -> （width，height）
6、视口变换：
投影变换后的（-1，1）正方体向（0，width）×（0，height）屏幕区域的变换，忽略Z方向的改变
在这里插入图片描述
2、将三角形打散成像素——采样
（1）为什么是三角形？
三角形是最基础的多边形；任何多边形多可以拆成三角形；三点一定在同一平面内；三角形的内外定义清晰；对三角形的三个点定义属性，内部的任一点属性都可计算渐变（三角形内部插值）
（2）判断像素和三角形的位置关系
对三角形采样就是判断像素中心是否位于三角形内，如果中心点在三角形外，则一定位于三角形三条边的同一侧，反之不成立。
方向判断用叉乘
P1Q×P1P2 < 0,说明P1Q位于P1P2左侧，同理可判断Q位于P0P1左侧，以及P2P0的左侧。
在这里插入图片描述
边缘条件的判断(比如像素中心位于边上) : 要不不作处理，要么特殊处理，在闫老师的课上不作处理。
（3）采样的加速方法：
1、boundingBox（包围盒）：通过三角形的三点坐标计算得出，不用遍历整个屏幕！
在这里插入图片描述
2、每一行只考虑最左和最右，多余一个元素都不计算

（4）抗锯齿：
发生锯齿的原因：采样率对于信号来讲不够高，产生信号走样

3、走样与反走样
从信号角度理解采样：采样就是重复原始信号的频谱
从信号角度理解走样：
走样的原因即采样率对于信号来讲不够高（信号变化速度快），导致图像的频谱出现交叉现象，结果就是导致锯齿。
在这里插入图片描述

（1）反走样的技术——增加采样率
属于物理手段。
如增加分辨率，像素和像素之间间隔小，采样率更高，频谱间隔大

（2）反走样的技术——滤波
如模糊滤波：先模糊后采样（顺序不能颠倒！），本质是降低信号的频率（减少高频）；
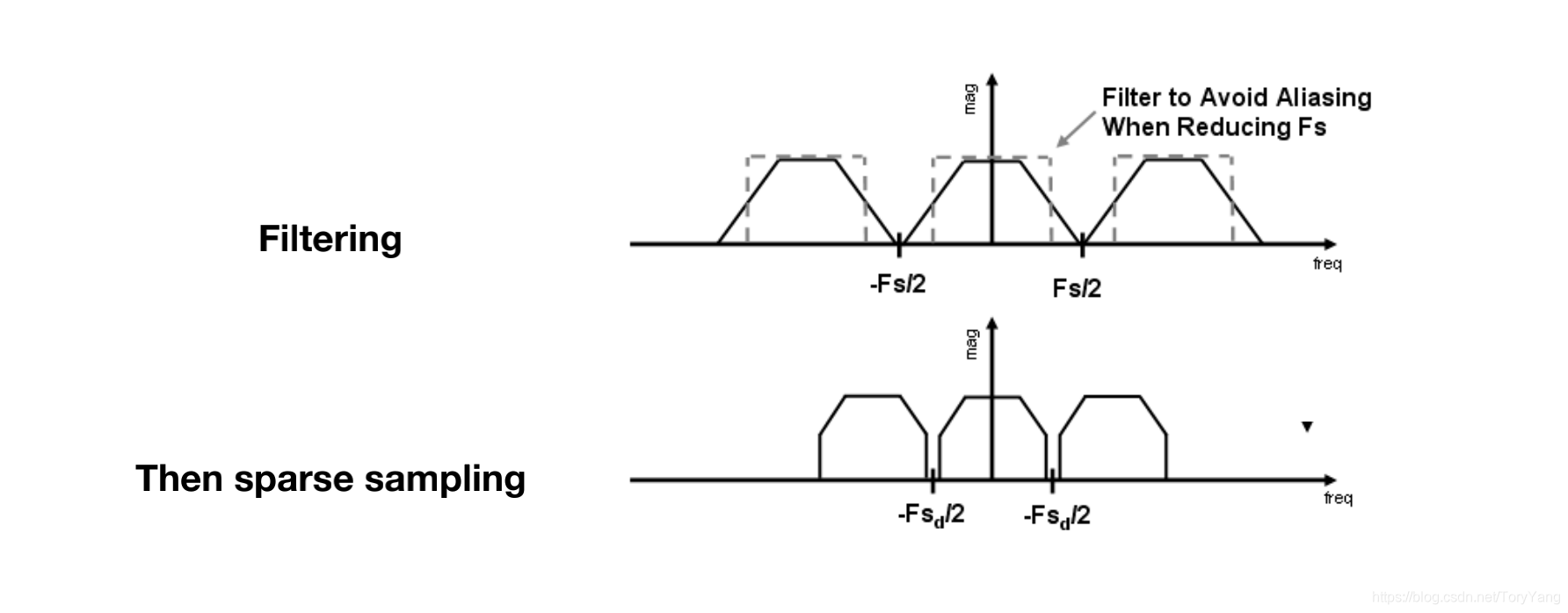
在这里插入图片描述
步骤
1、卷积，可看成是和周围的信号取平均 2、采样

（3）反走样的技术——超采样(Supersampling, MSAA)
将一个像素内分成更多的小部分，再分别判断是否位于三角形内，再卷积采样。
本质是对模糊处理的提升。
代价：提高计算量。

（4）FXAA与TAA
FXAA：快速近似抗锯齿，属于图像的后期处理，找到边界并替换
TAA：复用上一帧的结果抗锯齿

（5）DLSS
当小图拉大时会发生因采样率不够而细节缺失的现象，DLSS使用深度学习的方法”猜“出图像。

4、可见性（遮挡）问题——深度缓存（Z-buffering）
（1）画家算法：
即所有物体，计算深度（O( $n l o g n$ )）,按照深度顺序，从远到近依次渲染。
但深度的定义是个问题，而且有些物体之间不好明确深度关系，如下图：
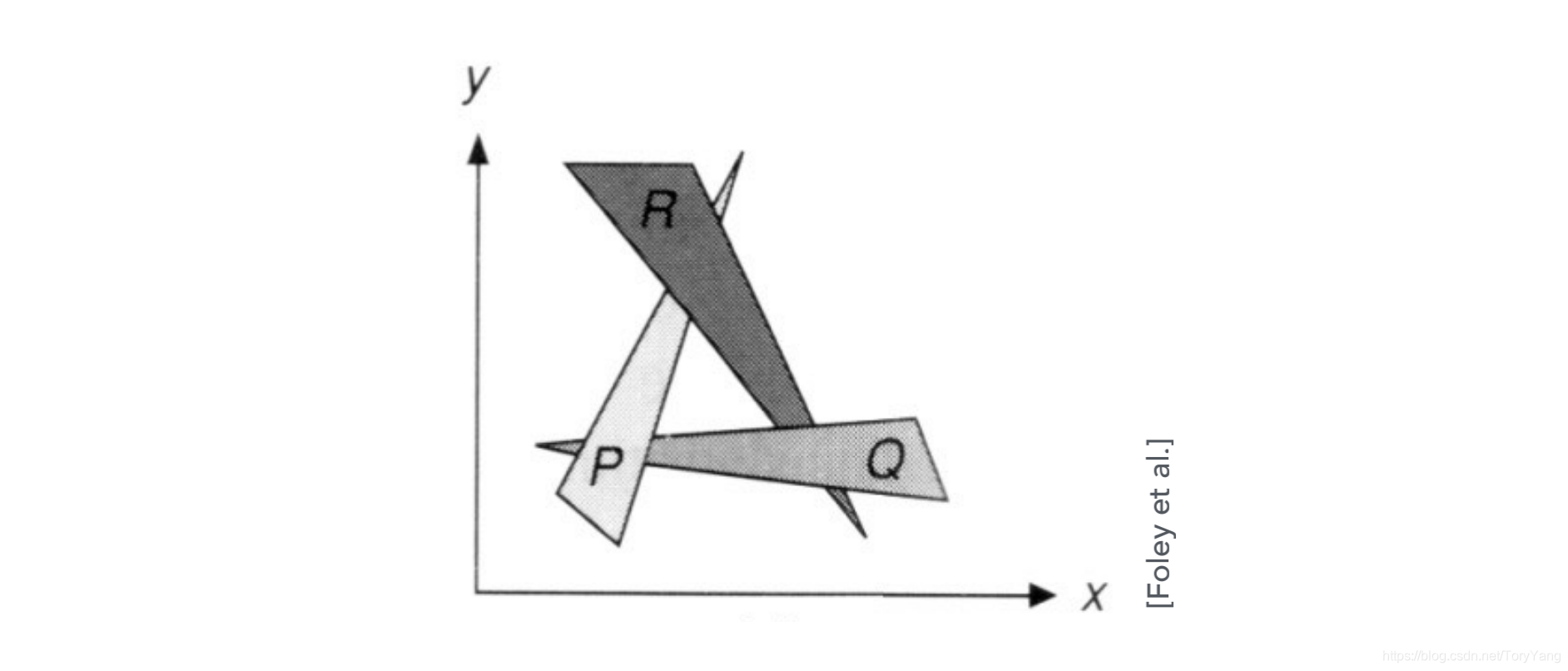
在这里插入图片描述
因此在图形学中不能使用画家算法。
（2）深度缓存（Z-buffer）：
1、思想：画家算法是对每个物体深度进行排序，而z-buffer则是对每个像素的深度进行排序，将排序结果存储在深度缓存（depth buffer）中，根据深度缓存对进行光栅化。
在Games101课程中，规定越远z越大，越近z越小（与之前规定的z意义不同）。
2、如何计算得到像素深度？
在这里插入图片描述
特点：与扫描三角形的顺序无关（假设不会有两个三角形在同一个像素拥有相同的深度，实际也类似，因为浮点数难以判等）。另外在MSAA中，一个像素被分成多个采样点，则是分别对每个采样点进行判断。

作业二

作业2要求实现三角形光栅化的流程：
（1）计算boundingBox
（2）遍历boundingBox包围的点，并判断是否在三角形内
（3）如果点在三角形内，得到点的深度（插值方法已给出），与深度缓存中的相比较，如果小于，则更新深度缓存，并在屏幕上显示该点

代码：
1、计算boundingBox：

int x_l = std::floor(std::min(v[0][0], std::min(v[1][0], v[2][0])));
int x_r = std::ceil(std::max(v[0][0], std::max(v[1][0], v[2][0])));
int y_b = std::floor(std::min(v[0][1], std::min(v[1][1], v[2][1])));
int y_t = std::ceil(std::max(v[0][1], std::max(v[1][1], v[2][1])));

2、判断点是否位于三角形内：

static bool insideTriangle(int x, int y, const Vector3f* _v)
{   //如果一个点P在三角形ABC内部，即AB*AP,BC*AP,CA*AP,叉乘符号均相同。Vector2f point(x, y);Vector2f AB = _v[1].head(2) - _v[0].head(2);Vector2f BC = _v[2].head(2) - _v[1].head(2);Vector2f CA = _v[0].head(2) - _v[2].head(2);Vector2f AP = point - _v[0].head(2);Vector2f BP = point - _v[1].head(2);Vector2f CP = point - _v[2].head(2);return    AB[0] * AP[1] - AB[1] * AP[0] > 0&& BC[0] * BP[1] - BC[1] * BP[0] > 0&& CA[0] * CP[1] - CA[1] * CP[0] > 0;}

3、遍历boundingBox，如果点位于三角形内：

 //(2)遍历bounding boxfor(int x = x_l ; x <= x_r ; x++)for(int y = y_b ; y <= y_t ; y++) {if(insideTriangle(x + 0.5, y + 0.5, t.v)) { //判断像素中心是否位于三角形内//获取该点的深度，插值计算方法已封装好auto[alpha, beta, gamma] = computeBarycentric2D((float)x + 0.5f, (float)y + 0.5f, t.v);float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();z_interpolated *= w_reciprocal;//将深度与深度缓存中的相比较，如果小于则更新深度缓存并在屏幕上画出if (depth_buf[get_index(x, y)] > z_interpolated) {Vector3f color = t.getColor();Vector3f point(3);point << (float)x, (float)y, z_interpolated;depth_buf[get_index(x, y)] = z_interpolated;set_pixel(point, color);}}}