本文主要是介绍机器学习:多项式拟合分析中国温度变化与温室气体排放量的时序数据,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 1、前言
- 2、定义及公式
- 3、案例代码
- 1、数据解析
- 2、绘制散点图
- 3、多项式回归、拟合
- 4、注意事项
1、前言
当分析数据时,如果我们找的不是直线或者超平面,而是一条曲线,那么就可以用多项式回归来分析和预测。
2、定义及公式
多项式回归可以写成:
Y i = β 0 + β 1 X i + β 2 X i 2 + . . . + β k X i k Y_{i} = \beta_{0} +\beta_{1}X_{i}+\beta_{2}X_{i}^2+...+\beta_{k}X_{i}^k Yi=β0+β1Xi+β2Xi2+...+βkXik
例如二次曲线:
Y = a X + b X 2 + c Y=aX+bX^2+c Y=aX+bX2+c
3、案例代码
1、数据解析
首先有1961年至2017年我国地表温度变化和温室气体排放量的时间序列数据,前十条数据如下。
| temp | emissions |
|---|---|
| 0.257 | 5635838102 |
| -0.142 | 6075180207 |
| 0.288 | 6510697811 |
| -0.028 | 6946401541 |
| 0.076 | 7421082166 |
| 0.18 | 7942541079 |
| -0.286 | 8374764636 |
| -0.414 | 8842570279 |
| -0.22 | 9418514950 |
2、绘制散点图
对于该数据我们先通过绘制散点图,这可以看出该数据适用于什么模型。
import matplotlib.pyplot as plt
import xlrd
import numpy as np
# 载入数据,打开excel文件
ExcelFile = xlrd.open_workbook("sandian.xls")
sheet1 = ExcelFile.sheet_by_index(0)
x = sheet1.col_values(0)
y = sheet1.col_values(1)
# 将列表转换为matrix
x = np.matrix(x).reshape(48, 1)
y = np.matrix(y).reshape(48, 1)# 划线y
plt.title("Epidemic and Dow Jones data analysis")
plt.xlabel("new cases")
plt.ylabel("Dow Jones Volume")
plt.plot(x, y, 'b.')
plt.show()
上述使用xlrd方式不建议使用,简单了解即可,正常我们会使用下述更为方便且稳定的pandas来读取csv文件,这会大大简洁我们的代码并减少工作量。当然结果也是一样的。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pdx = pd.read_csv('china.csv')['emissions']
y = pd.read_csv('china.csv')['temp']
# 划线y
plt.title("temp and emission")
plt.xlabel("emissions change")
plt.ylabel("temp change")
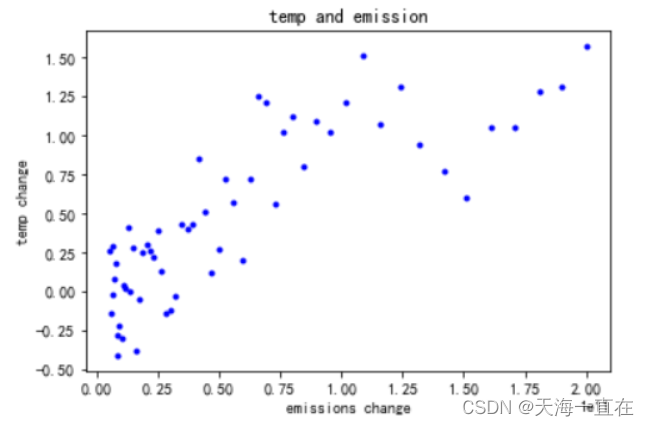
plt.plot(x, y, 'b.')
plt.show()
如图所示很明显,在排放量变化达到1.5(1e11)时,斜率发生了改变,因此我们可以判断这是一个多项式模型。
3、多项式回归、拟合
通过散点图的趋势,我们首先选择拟合3次来防止过拟合和欠拟合。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.metrics import r2_score
from matplotlib.font_manager import FontProperties # 导入FontPropertiesfont = FontProperties(fname="simhei.ttf", size=14) # 设置字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] =Falsex = pd.read_csv('china.csv')['emissions']
y = pd.read_csv('china.csv')['temp']# 进行多项式拟合(这里选取3次多项式拟合)
z = np.polyfit(x, y, 3) # 用3次多项式拟合# 获取拟合后的多项式
p = np.poly1d(z)
print(p) # 在屏幕上打印拟合多项式# 计算拟合后的y值
yvals=p(x)# 计算拟合后的R方,进行检测拟合效果
r2 = r2_score(y, yvals)
print('多项式拟合R方为:', r2)# 计算拟合多项式的极值点。
peak = np.polyder(p, 1)
print(peak.r)# 画图对比分析
plot1 = plt.plot(x, y, '*', label='初始值', color='red')
plot2 = plt.plot(x, yvals, '-', label='训练值', color='blue',linewidth=2)plt.xlabel('温室气体排放量',fontsize=13, fontproperties=font)
plt.ylabel('温度变化',fontsize=13, fontproperties=font)
plt.legend(loc="best")
plt.title('中国温室气体排放量与地表温度变化的关系')
plt.show()
最后结果如下图
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-go17Atvf-1681182766850)(C:\Users\Administrator\AppData\Roaming\Typora\typora-user-images\image-20230411105218629.png)]](https://img-blog.csdnimg.cn/ed3509076d154912a7bd5c19a2223eba.png)
3 2
3.002e-34 x - 1.351e-22 x + 2.284e-11 x - 0.2613
多项式拟合R方为: 0.7468687074304835
[1.50000065e+11+5.34488173e+10j 1.50000065e+11-5.34488173e+10j]
我们发现,这并不符合我们的预期,因为温室气体排放量在1.5(1e11)时,散点图趋势有明显的凹陷,而使用三次拟合并不能让曲线拟合到散点上。所以我们将 z = np.polyfit(x, y, 4)中的3改为4,来进行四次拟合。
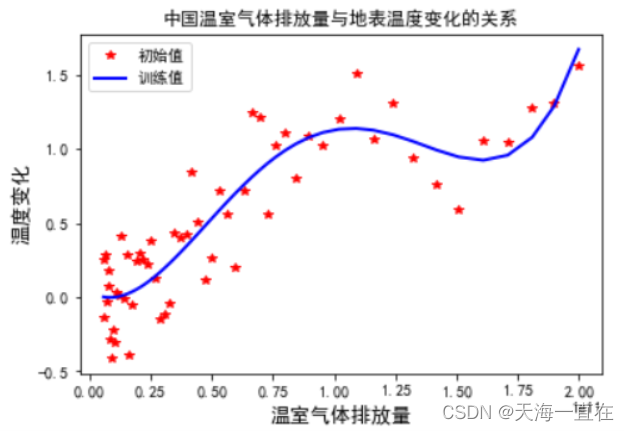
这样就达到了我们的预期效果,并输出我们的多项式回归公式。
4 3 2
1.702e-44 x - 6.273e-33 x + 6.634e-22 x - 9.696e-12 x + 0.03595
多项式拟合R方为: 0.7962406171380259
[1.60734484e+11 1.07514523e+11 8.24309615e+09]
我们可以得到数学模型:
Y = 1.702 ∗ 1 0 − 44 X − 6.273 ∗ 1 0 − 33 X + 6.634 ∗ 1 0 − 22 X − 9.696 ∗ 1 0 − 12 X + 0.03595 Y=1.702*10^{-44}X -6.273*10^{-33}X + 6.634*10^{-22}X-9.696*10^{-12}X +0.03595 Y=1.702∗10−44X−6.273∗10−33X+6.634∗10−22X−9.696∗10−12X+0.03595
4、注意事项
from matplotlib.font_manager import FontProperties # 导入FontProperties
font = FontProperties(fname="simhei.ttf", size=14) # 设置字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] =False
这些代码用于显示汉字标题,这需要你的本机中有一个汉字字体文件,simhei.ttf或其他字体文件。
如果需要引入,在第二行中指定文件路径。
这篇关于机器学习:多项式拟合分析中国温度变化与温室气体排放量的时序数据的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




