[Laplace Deformation]拉普拉斯网格变形--理论

这次Laplace Deformation的博客分为两个部分，理论和实现

实现（含代码）：https://blog.csdn.net/z136411501/article/details/107623248

 

参考：

Mesh模型的Laplace Deformation（网格形变 - 拉普拉斯形变） - 使用Eigen矩阵库

图形处理（三）简单拉普拉斯网格变形-Siggraph 2004

[图形学]拉普拉斯网格变形（Laplace Deformation）原理及复现

<<Polygon Mesh Processing>>阅读笔记（9）变形（Deformation）

这四篇博客（链接可点）看下来，基本变形流程的理解就没问题，其他人博客重复太多的定义介绍，我会省去简写。

 

Laplacian Mesh Processing.Olga Sokrine.EG2005   (paper原文已放百度云，强推，解释了推导变形的数学原理，why do that?)

链接：https://pan.baidu.com/s/1gsbof7yw8iAhkm4rkNWlNw 提取码：3lqp

 

以下出现的部分图表公式及文字表达均引用自上述链接及paper

一.拉普拉斯网格变形是什么

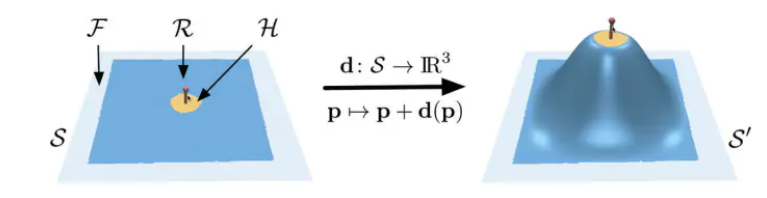
  一图以蔽之，左图S是初始网格，右图S'是变形后的网格。

  F，淡蓝色区域，是S的子区域，固定初始位置不变，不参与变形。

  R, 深蓝色与黄色区域，ROI区域，是位置改变的区域，其中（差集R-H）区域参与变形计算

  H, 黄色区域，olga Sokrine称其为Handle Vertices，形象理解为用手拽着移动的区域。

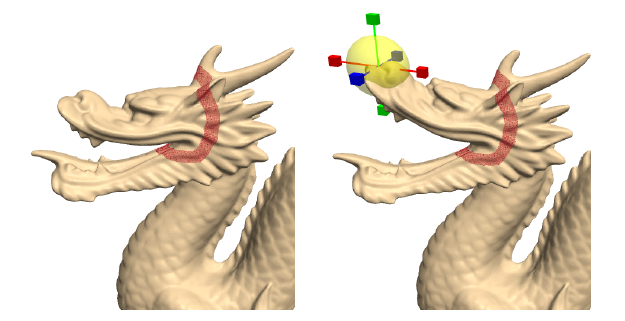
这是paper原文里的一张图，红色带确定参与变形的区域R，黄色球确定Handle区域H，拽着黄色球往上拖，差集R-H区域随之改变。

整个操作流程可以理解为，选择一张网格S,固定住他的边缘F,用手拽着H向上移动，同时差集R-H区域的顶点的新位置由拉普拉斯网格变形方程计算。

二.数学原理

2.1 拉普拉斯坐标

  由上两个例子可以看出，网格变形的一个需求就是要保证局部的细节特征尽量不变，而常规的笛卡尔坐标只保存了顶点的空间信息，这时引入拉普拉斯坐标（δ-Coordinate）的概念。我们将每个顶点的笛卡尔坐标转换为拉普拉斯坐标，再来思索问题。

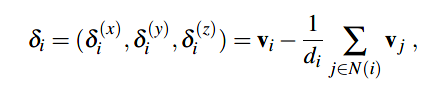
  拉普拉斯坐标，其数学意义为一个顶点的笛卡尔坐标和这个点所有邻接点的笛卡尔坐标的加权平均，物理意义为拉普拉斯坐标能够记录模型的局部细节特征。

  当网格形变后，我们希望网格的局部信息不要被破坏，换成坐标的说法就是，网格上顶点的笛卡尔坐标变了，但是我们希望网格上所有点的拉普拉斯坐标没变，也就是点和点的相对位置关系没变。

  补充：paper原文解释了为什么δ坐标能记录局部细节特征。

从微分几何的角度，拉普拉斯坐标写成下式，

上式可以看成是下式曲线积分的离散近似

下图为上面两个公式的几何意义示意，左图为离散表示，右图为连续的微积分表示

对于右图，γ是嵌在surface表面的封闭黑色曲线，|γ|为曲线的长度。

现在我们假设，当连续微积分的微分区域γ无限小时，γ近似于一个微圆，（修正paper中的公式如下，红框区域应该是叉乘，而不是点乘，否则解释不了等于等式右边，），左边微积分等于该点的平均曲率H(vi)与该点的法线ni的乘积。所以这个微积分的值的标量等于平均曲率，方向等于法线。

ps:原文没有解释这个等式，以下是我的自己理解：

假设γ近似于一个半径无穷小（R→0）的平面圆，叉积的数学意义为求面积，则

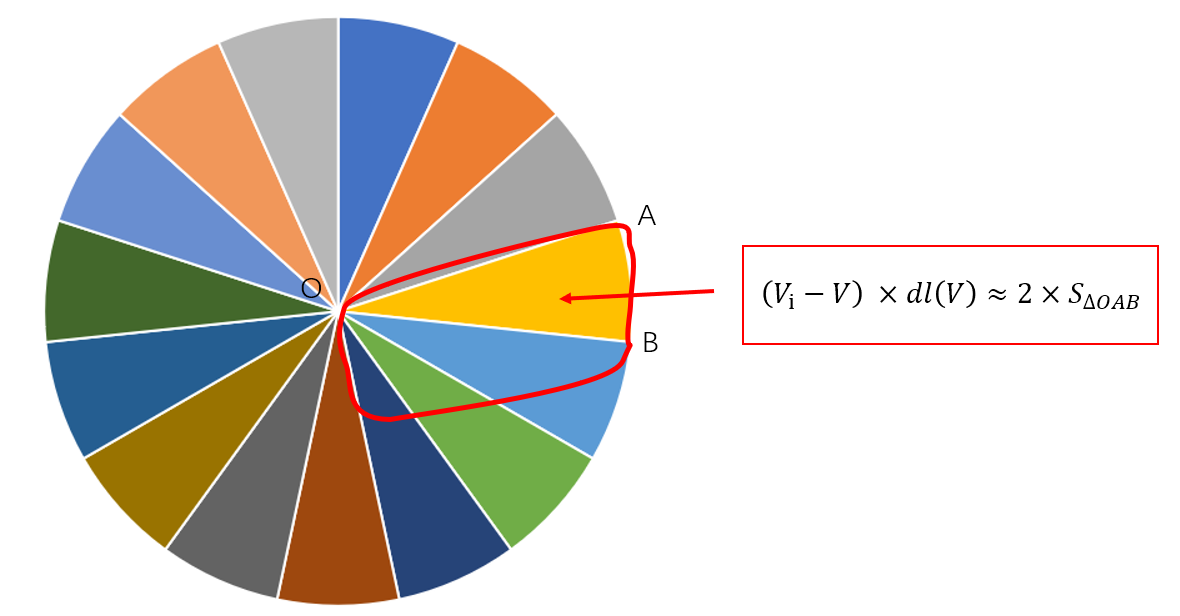
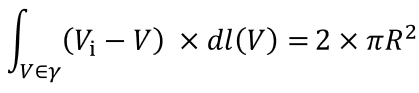
|γ|为曲线的长度，即这个圆的周长，

因为Vi与V为矢量，所以微积分的方向为该点的法向（mesh一个顶点的法线方向为这个顶点与周围三角形的叉乘矢量和的方向的单位化和，具体可以百度）。

所以

等式右边H(Vi)表示该点的平均曲率，曲率的解释，这个https://www.zhihu.com/question/25952605解释的很好，

把γ看作为一个平面微圆，因为是平面的，所以这个点的曲率H(vi)无穷小，接近于0。又因为R→0，所以

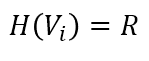
证毕。所以直观地讲，δ坐标能表示局部形状的特征

目前为止，拉普拉斯的坐标计算均采用的是平均加权，当然有其他的加权方法，可以看其他文章的介绍

图形处理（三）简单拉普拉斯网格变形-Siggraph 2004

2.2 矩阵计算

 用一个矩阵 L 将mesh网格所有顶点从笛卡尔坐标转到拉普拉斯坐标，即,这个矩阵矩阵很容易想到为

I为单位矩阵（nxn，n为网格顶点的数目）,D为对角矩阵，其中Dii=di,di为第i个顶点的相邻顶点的数目，A为邻接矩阵

这里paper作者提出，为方便起见，一般考虑使用L的对称形式，Ls，参与之后的计算

Ls图表示意如下，

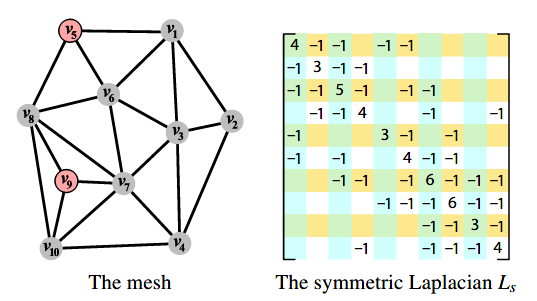
但有了L或Ls,我们不能像 一样，简单的由拉普拉斯坐标δ反推出笛卡尔坐标V ，因为L或Ls矩阵非满秩，不可逆。（用右上图的Ls矩阵示例，矩阵每一行的累加值为0，非满秩，这就表明了至少存在一个非零的特征向量，而这个特征向量并不是我们想要的。）

作者也指出

k是连通分量的个数。左上图示例的连通分量为1，所以rank(L) = 10-1 = 9

  补充：连通分量

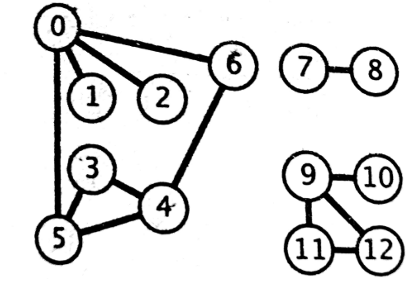
这个图有三个连通分量，0-6，7-8，9-12

注意，危！所以，只要给定一个顶点 Vi 变化后的拉普拉斯坐标与笛卡尔坐标。数学意义上就等价于丢掉了LV = δ中，L矩阵的第i行与第i列，这样在假使mesh联通分量只有1的情况下，矩阵满秩，可求唯一解。

所以只要有1个锚点（笛卡尔坐标位置已知的点，笛卡尔坐标是未知数，因为要逆推笛卡尔坐标的值）就能解方程。但通常在方程组中放置更多的锚点，即固定锚点和可移动的handle锚点。（作者在后期提到了放置更多锚点的原因是为了加速求解矩阵时，矩阵的稳定性考虑，但我觉得其他几个博客提到的原因也很有道理）

现在就可以列出我们的新方程组Ax=b,A是加过锚点之后的矩阵，b是更改过的拉普拉斯坐标值，x是我们要求的笛卡尔坐标值。

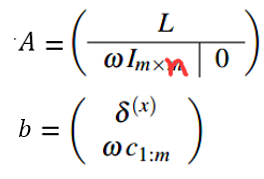
w是锚点的权，w>0，一般设为1。I是一个mxn的类单位矩阵，m为锚点的数目，n为网格顶点的数目，I的每一行只有一个非零元素，其值为1。c1:m 已知的该锚点的笛卡尔坐标。

下图为加了两个锚点后的Ls矩阵

所以到这一步位置，Ax=b是一个超定方程组，方程组秩等于列秩n < 行数（m+n）,所以该超定方程组存在唯一最小二乘解，即

解为

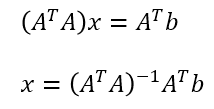
x就是最终求出来的变形后网格的新笛卡尔坐标的集合。

这里是超定方程组最小二乘解的推导过程 https://www.cnblogs.com/narjaja/p/9304472.html