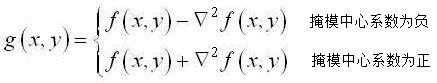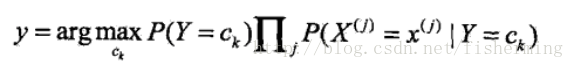laplace专题

Laplace变换-3

回忆#常见函数的Laplace变换： t z − 1 ↦ Γ ( z ) s z t^{z-1} \mapsto \frac{\Gamma(z)}{s^{z}} tz−1↦szΓ(z) （要求 R e ( z ) > 0 \mathrm{Re}(z)>0 Re(z)>0） e a t ↦ 1 s − a e^{at} \mapsto \frac{1}{s-a} eat↦s−a1 c

Halcon滤波器 laplace 算子

Halcon滤波器 laplace 算子使用laplace 算子对图像进行二次求导，会在边缘产生零点，因此该算子常常与zero_crossing算子配合使用。求出这些零点，也就得到了图像的边缘。同时，由于laplace算子对孤立像素的响应要比对边缘或线的响应更强烈，因此在检测之前应先进行去噪处理。该算子的原型如下： laplace (Image: ImageLaplace : Result

[足式机器人]Part2 Dr. CAN学习笔记-动态系统建模与分析 Ch02-4 拉普拉斯变换（Laplace）传递函数、微分方程

本文仅供学习使用本文参考： B站：DR_CAN Dr. CAN学习笔记-动态系统建模与分析 Ch02-4 拉普拉斯变换（Laplace）传递函数、微分方程 1. Laplace Transform 拉式变换2. 收敛域（ROC）与逆变换（ILT） 1. Laplace Transform 拉式变换 f ( t ) → F ( s ) f\left( t \righ

[Laplace Deformation]拉普拉斯网格变形--理论

这次Laplace Deformation的博客分为两个部分，理论和实现实现（含代码）：https://blog.csdn.net/z136411501/article/details/107623248 参考： Mesh模型的Laplace Deformation（网格形变 - 拉普拉斯形变） - 使用Eigen矩阵库图形处理（三）简单拉普拉斯网格变形-Siggraph 2004 [图

OpenCV笔记：图像边缘检测Sobel，Laplace，Canny

边缘提取时保留图像灰度变化剧烈的区域，从数学上,最直观的方法是微风,对于数字图像来说就是差分，从信号处理的角度来看,就是用高通滤波器，保留高频信号。以下程序用Sobel算子、Laplace算子、Canny算子实现图像的边缘检测。注：cvSobel只用于单通道图像变换，如对彩色图像进行cvSobel处理，可分别对每一通道图像进行cvSobel，再转为彩色图像。 ===========

余切拉普拉斯算子推导 cotangent Laplace-Beltrami operator

欢迎关注更多精彩关注我，学习常用算法与数据结构，一题多解，降维打击。参考自polygon mesh proccessing这本书基本思路及原理余切拉普拉斯算子是一种考虑了网格底层几何联系的一种算子，在网格平滑，参数化等算法中经常被用到。它是受到了有限元思绪启发推导出来的。用到有限元中的散度定理。目标是对三角平面分片线性函数的梯度的散度进行面积积分。散度定理如下，对散度的面积分，

图像处理笔记（二）：Laplace算子及LOG

图像处理笔记（二）：Laplace算子及LOG 由上一篇介绍，我们可以知道在一阶导数的极值位置，二阶导数为0。所以我们也可以用这个特点来作为检测图像边缘的方法。在图像处理，我们知道经常把Laplace算子作为边缘检测之一。 Laplace算子定义：一个二维图像函数的拉普拉斯变换是各向同性的二阶导数，定义如下：拉普拉斯算子是最简单的各向同性微分算子，它具有旋转不变性。推导：二

Opencv图像增强算法实现(直方图均衡化、Laplace、Log、Gamma)

原文链接: https://loopvoid.github.io/2017/02/21/Opencv%E5%9B%BE%E5%83%8F%E5%A2%9E%E5%BC%BA%E7%AE%97%E6%B3%95%E5%AE%9E%E6%B3%95/ 增强图像中的有用信息，它可以是一个失真的过程，其目的是要改善图像的视觉效果，针对给定图像的应用场合，有目的地强调图像的整体或局部特性，将原来不清晰

$Harris-Laplace与Harris-Affine原理$

laplace专题

Laplace变换-3

Halcon滤波器 laplace 算子

[足式机器人]Part2 Dr. CAN学习笔记-动态系统建模与分析 Ch02-4 拉普拉斯变换（Laplace）传递函数、微分方程

[Laplace Deformation]拉普拉斯网格变形--理论

OpenCV笔记：图像边缘检测Sobel，Laplace，Canny

余切拉普拉斯算子推导 cotangent Laplace-Beltrami operator

图像处理笔记（二）：Laplace算子及LOG

Opencv图像增强算法实现(直方图均衡化、Laplace、Log、Gamma)

Harris-Laplace与Harris-Affine原理

Laplace(拉普拉斯)算子

【转】朴素贝叶斯分类与Laplace平滑

dog算子处理图片边界matlab代码,圖像邊緣檢測——二階微分算子（上）Laplace算子、LOG算子、DOG算子（Matlab實現）...