EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks（2020）

本文主要是介绍EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks（2020），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

原文链接
源代码

-

本文中的宽度可以理解为通道数，一般认为高的FLOPS更好，因为计算效率快
但本文中作者认为低的浮点运算数（FLOPS）更好是因为较低的FLOPS意味着模型在执行推理或训练时需要更少的计算资源，这对于在计算能力有限的设备上部署模型或在大规模应用中效率更高都是很重要的。通过降低FLOPS，可以在保持性能的同时减少模型的复杂度，这有助于提高模型的速度和效率

Abstract

卷积神经网络(ConvNets)通常是在固定的资源预算下开发的，如果有更多的资源可用，则可以扩展以获得更好的准确性。在本文中，我们系统地研究了模型缩放，并确定仔细平衡网络深度，宽度和分辨率可以带来更好的性能。基于这一观察结果，我们提出了一种新的缩放方法，该方法使用简单而高效的复合系数对深度/宽度/分辨率的所有维度进行均匀缩放。我们证明了该方法在扩展MobileNets和ResNet方面的有效性
为了更进一步，我们使用神经架构搜索来设计一个新的基线网络，并将其扩展以获得一系列模型，称为EffentNets，它比以前的ConvNets具有更好的准确性和效率。特别是，我们的EfficientNet-B7在ImageNet上达到了最先进的84.3%的top-1精度，同时比现有最好的ConvNet小8.4倍，推理速度快6.1倍。我们的EfficientNets在CIFAR-100(91.7%)、Flowers(98.8%)和其他3个迁移学习数据集上的迁移效果也很好，达到了最先进的准确率，参数减少了一个数量级

1. Introduction

扩大卷积神经网络被广泛用于获得更好的准确率。例如，ResNet (He et al.， 2016)可以通过使用更多的层从ResNet-18扩展到ResNet-200;最近，GPipe (Huang et al.， 2018)通过将基线模型放大四倍，实现了84.3%的ImageNet top-1精度

diss former method

然而，扩大卷积神经网络的过程从未被很好地理解，目前有很多方法可以做到这一点。最常见的方法是通过深度(He et al.， 2016)或宽度(Zagoruyko & Komodakis, 2016)来扩展卷积神经网络。另一种不太常见但越来越流行的方法是按图像分辨率缩放模型(Huang et al.， 2018)。在以前的工作中，通常只缩放三个维度中的一个——深度、宽度和图像大小。虽然可以任意缩放两个或三个维度，但任意缩放需要繁琐的手动调优，并且仍然经常产生次优的精度和效率

our method

在本文中，我们想要研究和重新思考放大卷积神经网络的过程。特别是，我们研究了一个核心问题:是否有一种原则性的方法来扩大卷积神经网络，从而达到更好的准确性和效率?我们的实证研究表明，平衡网络宽度/深度/分辨率的所有维度是至关重要的，令人惊讶的是，这种平衡可以通过简单地以恒定的比例缩放每个维度来实现。在此基础上，我们提出了一种简单有效的复合标度方法。与传统的任意缩放这些因素的做法不同，我们的方法用一组固定的缩放系数统一地缩放网络宽度、深度和分辨率。例如，如果我们想使用2^N倍的计算资源，那么我们可以简单地将网络深度增加α N，宽度增加β N，图像大小增加γ N，其中α，β，γ是由原始小模型上的小网格搜索确定的常系数。图2说明了我们的缩放方法与传统方法之间的区别

(a)是一个基线网络示例;(b)-(d)为常规缩放，仅增加网络宽度、深度或分辨率的一个维度。(e)是我们提出的以固定比例均匀缩放所有三个维度的复合缩放方法

直观地说，复合缩放方法是有意义的，因为如果输入图像更大，那么网络需要更多的层来增加接受域，需要更多的通道来捕获更大图像上的更细粒度的模式。事实上，之前的理论(Raghu et al.， 2017;Lu et al.， 2018)和实证结果(Zagoruyko & Komodakis, 2016)都表明网络宽度和深度之间存在一定的关系，但据我们所知，我们是第一个对网络宽度、深度和分辨率这三个维度之间的关系进行实证量化的人

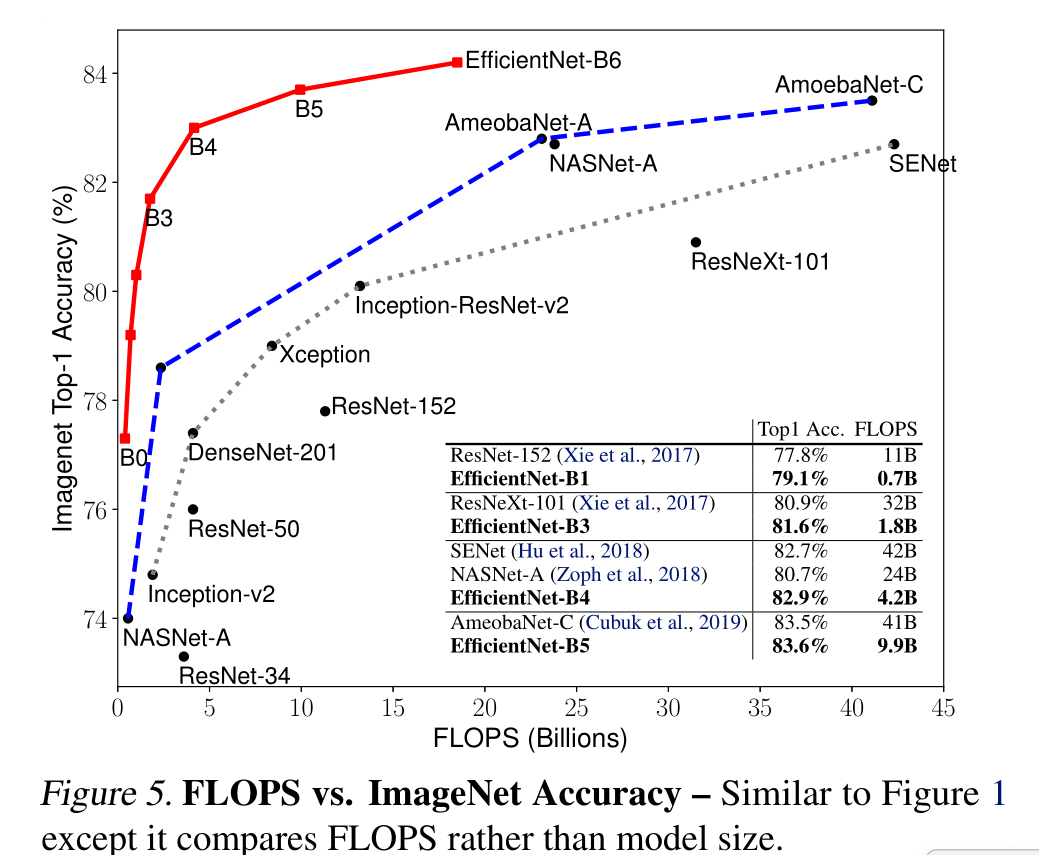
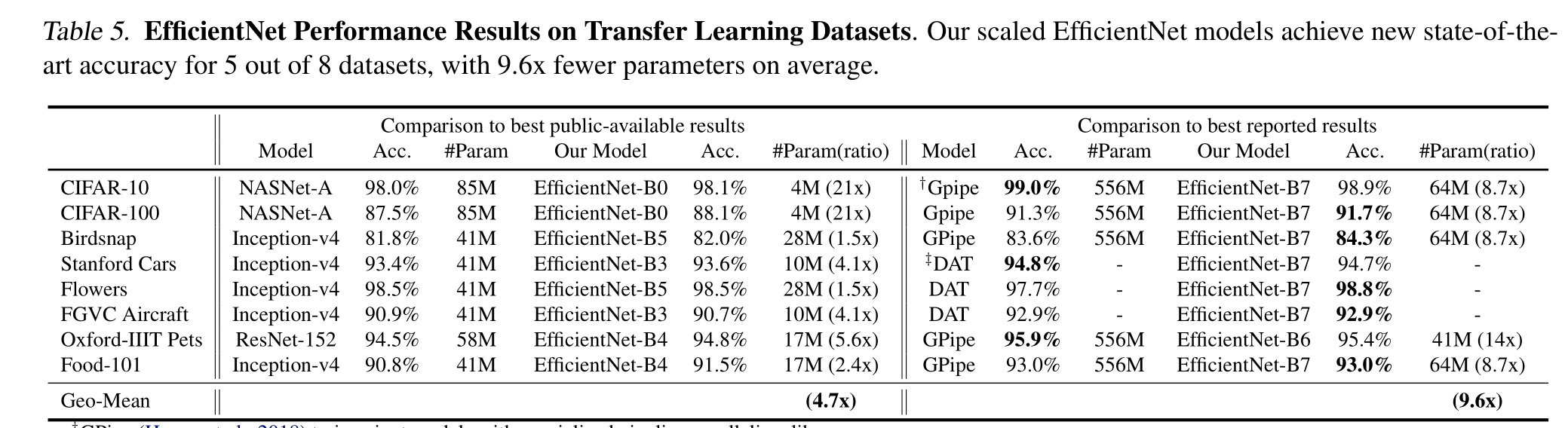
我们证明了我们的缩放方法在现有的mobilenet上工作得很好(Howard等人，2017;Sandler等人，2018)和ResNet (He等人，2016)。值得注意的是，模型缩放的有效性严重依赖于基线网络;更进一步，我们使用神经架构搜索(Zoph & Le, 2017;Tan et al.， 2019)开发一个新的基线网络，并将其扩展以获得一系列模型，称为EfficientNets。图1总结了ImageNet的性能，其中我们的EfficientNets明显优于其他ConvNets。特别是，我们的EfficientNet-B7超过了现有的最佳GPipe精度(Huang et al.， 2018)，但使用的参数减少了8.4倍，在参考上运行速度提高了6.1倍。与广泛使用的ResNet-50 (He et al.， 2016)相比，我们的EfficientNet-B4在FLOPS相似的情况下，将top-1的准确率从76.3%提高到83.0%(+6.7%)。除了ImageNet, EfficientNets在8个广泛使用的数据集中的5个上也能很好地传输并达到最先进的精度，同时比现有的ConvNets减少了高达21倍的参数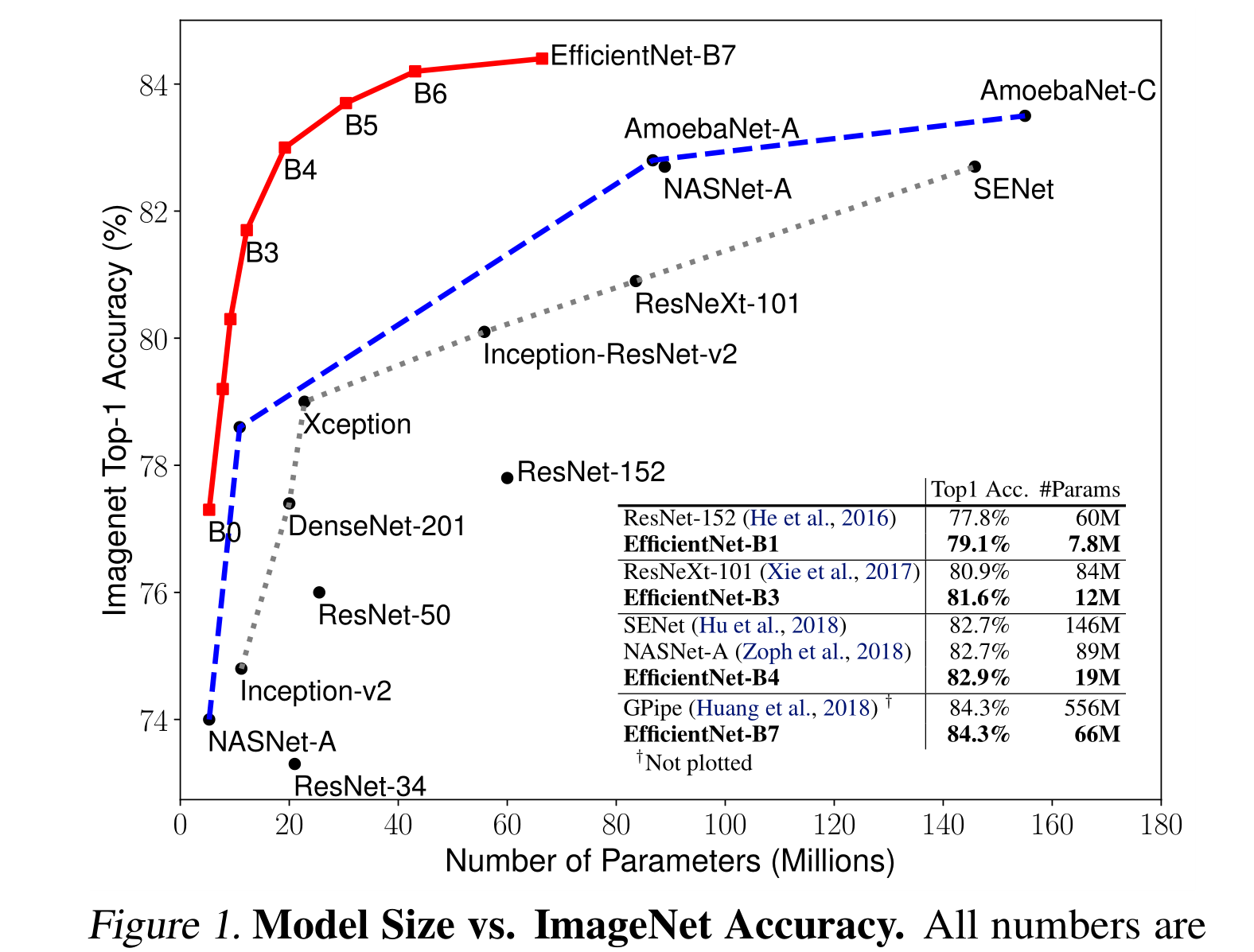

2. Related Work

简单夸赞了下前人的work，从精度、效率和模型缩放方面
在本文中，我们的目标是研究超大规模卷积神经网络的模型效率，以超越目前的精度。为了实现这一目标，我们采用模型缩放
网络深度和宽度对卷积神经网络的表达能力都很重要，但如何有效地扩展卷积神经网络以获得更好的效率和准确性仍然是一个悬而未决的问题。我们的工作系统地和经验地研究了网络宽度、深度和分辨率这三个维度的卷积神经网络缩放

3. Compound Model Scaling

我们将制定缩放问题，研究不同的方法，并提出我们的新缩放方法

3.1. 问题公式化

卷积层i可以定义为一个函数:Y i = F i (X i)，其中F i是算子，Y i是输出张量，X i是输入张量，张量的形状是<H i,W i,C i >1，其中，hi和wi为空间维度，ci为通道维度。卷积神经网络N可以用一个组合层的列表表示:N = F k ⊙…⊙f2 ⊙f1 (x1) = ⊙j = 1…k F j (x1)在实践中，ConvNet层通常被划分为多个阶段，每个阶段的所有层都共享相同的架构:例如，ResNet (He et al.， 2016)有五个阶段，每个阶段的所有层都具有相同的卷积类型，除了第一层执行下采样。因此，我们可以将ConvNet定义为:

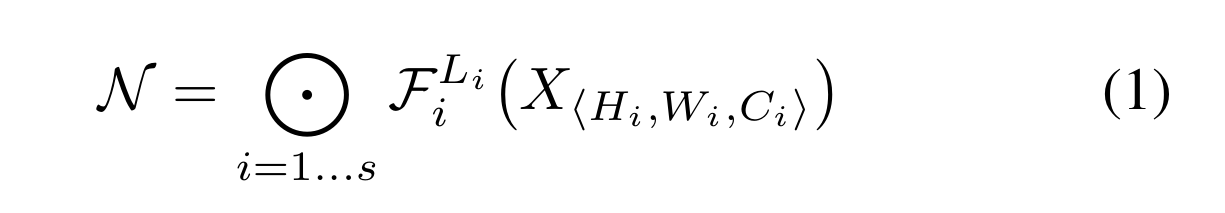
其中fl i i表示层F i在阶段i重复L i次，表示第i层输入张量X的形状。图2(a)展示了一个具有代表性的ConvNet，其中空间维度逐渐缩小，但通道维度逐层扩展，例如，从初始输入形状<224,224,3>到最后输出形状<7,7,512>

与常规的ConvNet设计不同，模型缩放试图扩展网络长度(L i)、宽度(C i)和/或分辨率(H i,W i)，而不改变基线网络中预定义的F i。通过固定F i，模型缩放简化了针对新资源约束的设计问题，但对于每一层探索不同的L i,C i,H i,W i仍然有很大的设计空间。为了进一步缩小设计空间，我们限制所有层必须以恒定比例均匀缩放。我们的目标是在任何给定的资源约束下使模型精度最大化，这可以表述为一个优化问题:

式中，w、d、r为缩放网络宽度、深度和分辨率的系数;F i、L i、H i、W i、C i是基线网络中预定义的参数(示例见表1)。

3.2. Scaling Dimensions

问题2的主要难点在于最优的d、w、r相互依赖，且在不同的资源约束条件下其值是变化的。由于这个困难，传统的方法主要是在以下一个维度上缩放卷积神经网络:

**深度(d)😗*缩放网络深度是许多卷积网络最常用的方法(He et al.， 2016;黄等人，2017;Szegedy等，2015;2016)。直觉是，更深层次的卷积神经网络可以捕获更丰富、更复杂的特征，并且可以很好地泛化新任务。然而，由于梯度消失问题，更深层的网络也更难以训练(Zagoruyko & Komodakis, 2016)。尽管跳跃连接(He et al.， 2016)和批处理归一化(ioffe&szegedy, 2015)等几种技术缓解了训练问题，但非常深的网络的精度增益减少了:例如，ResNet-1000具有与ResNet-101相似的精度，尽管它具有更多的层。图3(中)显示了我们对不同深度系数d的基线模型进行缩放的实证研究，进一步表明了非常深的卷积神经网络的精度回报递减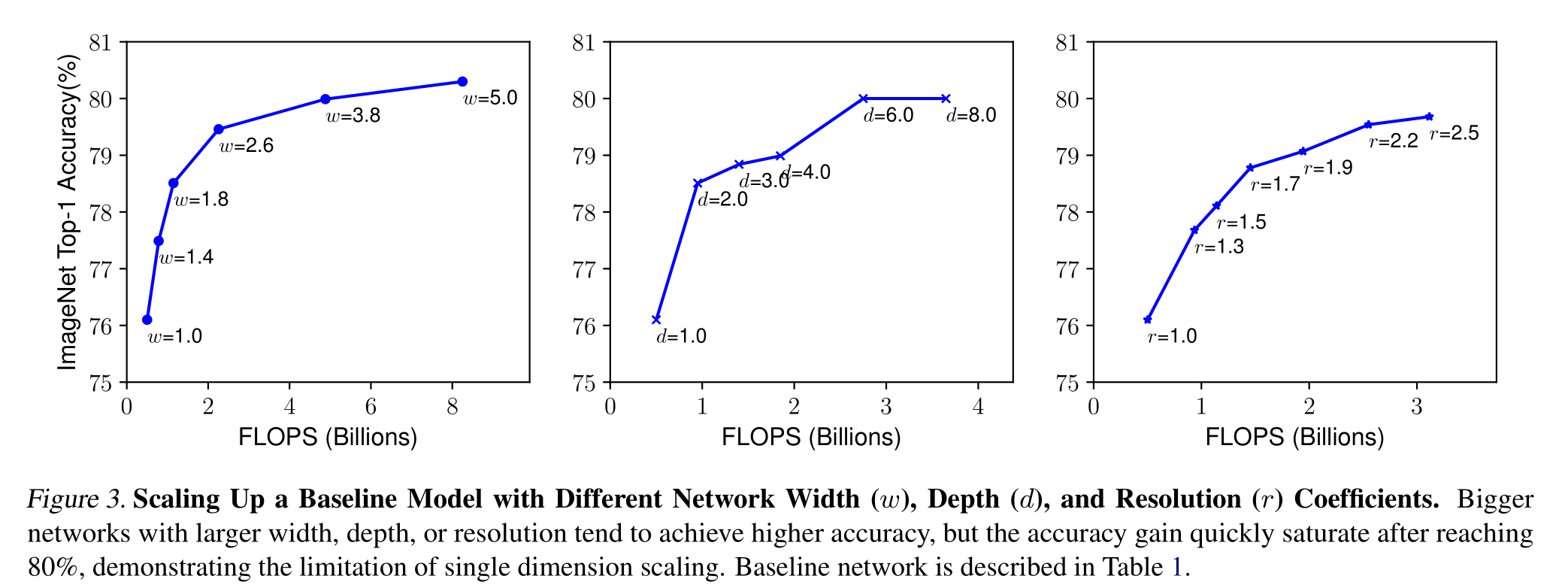

更大的网络，具有更大的宽度、深度或分辨率，往往可以获得更高的精度，但精度增益在达到80%后很快饱和，这表明了单维度缩放的局限性

宽度(w):通常用于缩放网络宽度小尺寸模型(Howard et al.， 2017;Sandler et al.， 2018;Tan et al.， 2019)正如(Zagoruyko & Ko-modakis, 2016)中所讨论的，更广泛的网络往往能够捕获更细粒度的特征，并且更容易训练。然而，极宽但较浅的网络往往难以捕获更高级的特征。我们在图3(左)中的经验结果表明，当网络变得更宽，w更大时，准确性很快饱和

分辨率®:使用更高分辨率的输入图像，ConvNets可以捕获更细粒度的模式。从早期ConvNets的224x224开始，现代ConvNets倾向于使用299x299 (Szegedy等人，2016)或331x331 (Zoph等人，2018)以获得更好的精度。最近，GPipe (Huang et al.， 2018)在480 × 480分辨率下实现了最先进的ImageNet精度。更高的分辨率，如600x600，也广泛用于目标检测卷积神经网络(He et al.， 2017;Lin等人，2017)。图3(右)显示了缩放网络分辨率的结果，其中更高的分辨率确实提高了精度，但对于非常高的分辨率，精度增益会降低(r = 1.0表示分辨率224x224, r = 2.5表示分辨率560x560)

通过以上分析，我们得出了第一个结论：
放大网络宽度、深度或分辨率的任何维度都可以提高精度，但对于更大的模型，精度增益会降低

3.3. Compound Scaling

我们通过经验观察到，不同的标度维度并不是相互独立的。直观地说，对于更高分辨率的图像，我们应该增加网络深度，这样更大的接受域可以帮助捕获在更大的图像中包含更多像素的相似特征。相应的，我们也应该在分辨率较高时增加网络宽度，以便在高分辨率图像中以更多的像素捕获更细粒度的图案。这些直觉表明，我们需要协调和平衡不同的缩放维度，而不是传统的单一维度缩放

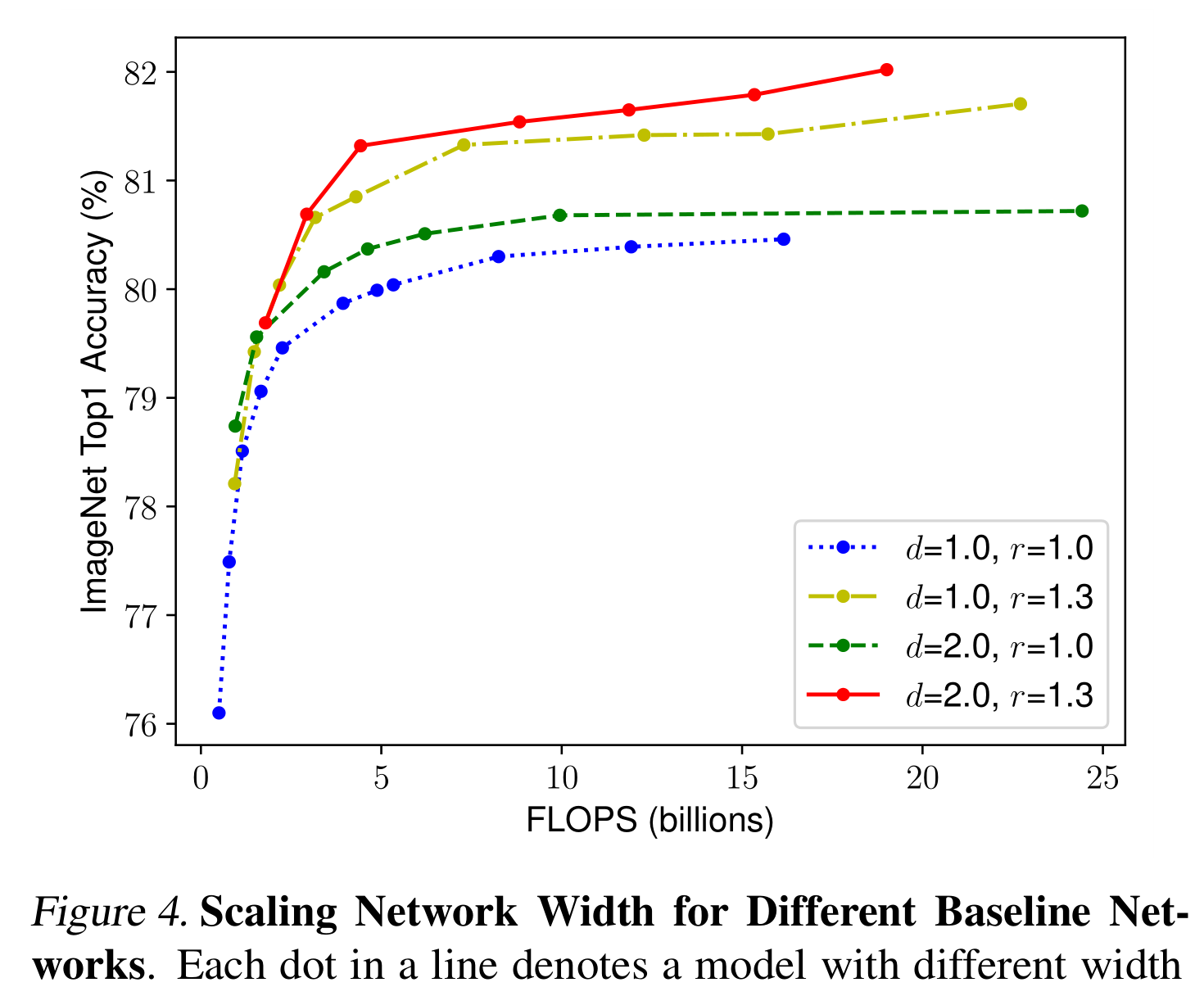
为了验证我们的直觉，我们比较了不同网络深度和分辨率下的宽度缩放，如图4所示。如果我们只缩放网络宽度w而不改变深度(d =1.0)和分辨率(r =1.0)，则精度很快饱和。在相同的FLOPS成本下，在更深(d =2.0)和更高的分辨率(r =2.0)下，宽度缩放可以获得更好的精度。这些结果将我们引向第二个观察结果:
为了追求更好的精度和效率，在卷积神经网络缩放过程中，平衡网络宽度、深度和分辨率的各个维度是至关重要的

事实上，之前的一些工作(Zoph et al.， 2018;Real et al.， 2019)已经尝试任意平衡网络宽度和深度，但它们都需要繁琐的手动调优
本文提出了一种新的复合缩放方法，该方法利用复合系数φ对网络宽度、深度和分辨率进行有原则的均匀缩放:

其中α，β，γ是可以通过小网格搜索确定的常数。直观地说，φ是一个用户指定的系数，它控制有多少资源可用于模型缩放，而α，β，γ分别指定如何将这些额外的资源分配给网络宽度，深度和分辨率

值得注意的是，规则卷积op的FLOPS与d, w, r成正比，即网络深度加倍将使FLOPS加倍，但网络宽度或分辨率加倍将使FLOPS增加四倍。由于卷积运算通常在卷积网络的计算成本中占主导地位，因此用公式3缩放卷积网络将使总FLOPS大约增加(α·β 2·γ 2 )φ。在本文中，我们约束α·β 2·γ 2≈2，使得对于任何新的φ，总FLOPS将大约增加2 ^φ

4. EfficientNet Architecture

由于模型缩放不会改变基线网络中的层算子F i，因此拥有一个良好的基线网络也至关重要。我们将使用现有的卷积神经网络来评估我们的缩放方法，但为了更好地展示我们的缩放方法的有效性，我们还开发了一个新的移动尺寸基线，称为EffientNet

受(Tan et al.， 2019)的启发，我们通过利用多目标神经架构搜索来开发基线网络，该搜索可优化准确性和FLOPS。里我们优化FLOPS而不是延迟，因为我们不针对任何特定的硬件设备。我们的搜索产生了一个高效网络，我们将其命名为EfficientNet-B0

表1显示了EfficientNet-B0的体系结构。它的主要构建块是移动反向瓶颈MBConv (San- dler et al.， 2018;Tan等人，2019)，我们还添加了挤压和激励优化(Hu等人，2018)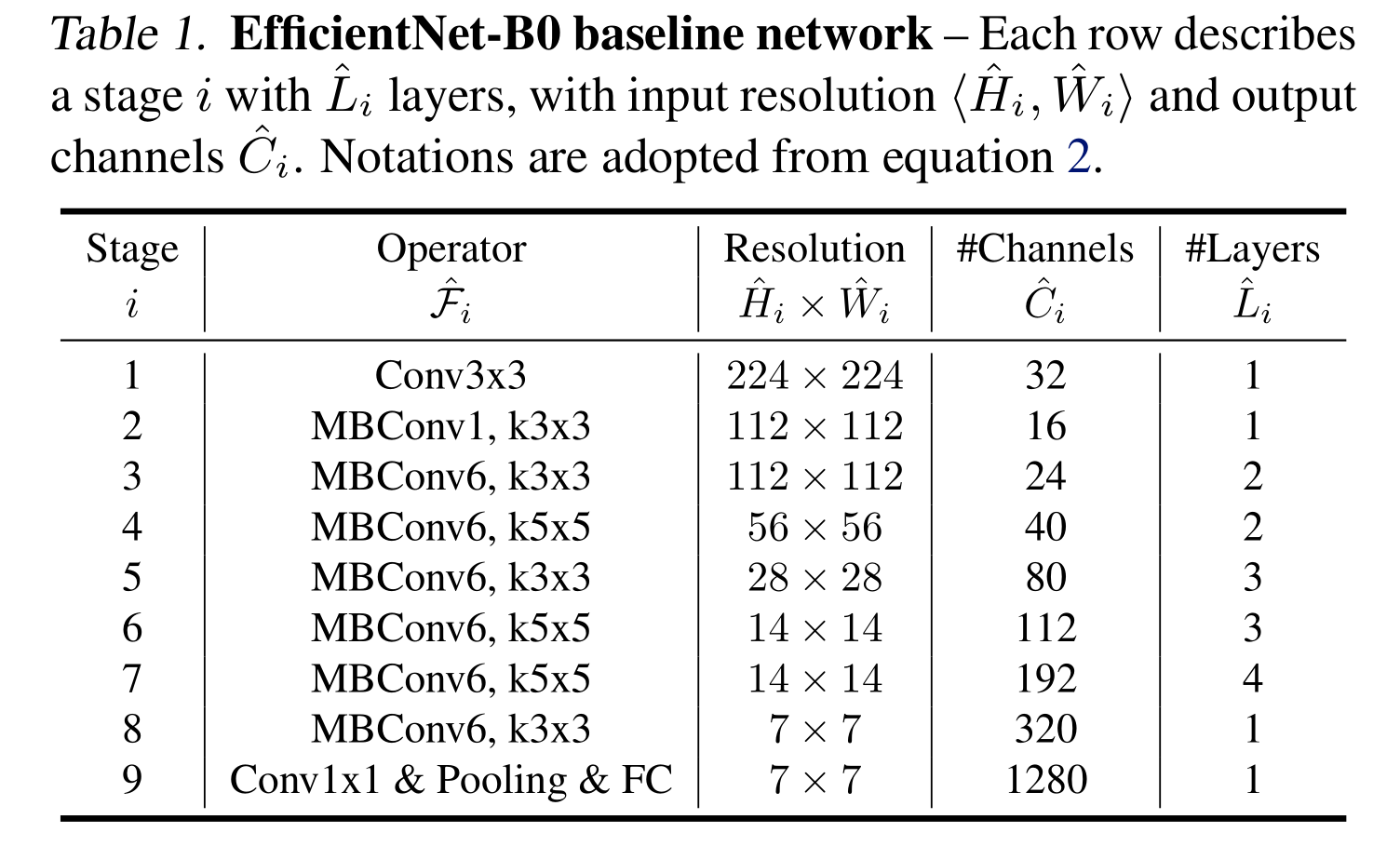
从基线EfficientNet-B0开始，我们采用复合扩展方法，分两个步骤进行扩展:
• 第一步:我们首先固定φ = 1，假设两倍以上的资源可用，并根据公式2和3进行α，β，γ的小网格搜索。特别地，我们发现在α·β 2·γ 2≈2的约束下，EfficientNet-B0的最佳值为α = 1.2，β = 1.1，γ = 1.15

•步骤2:然后我们将α，β，γ固定为常数，并使用公式3缩放具有不同φ的基线网络，以获得EfficientNet-B1到B7(详细信息见表2)

即先固定φ ，计算α、β、γ，然后固定α、β、γ，计算φ
值得注意的是，通过在大型模型周围直接搜索α，β，γ可以获得更好的性能，但是在大型模型上搜索成本会变得非常昂贵。我们的方法解决了这个问题，只在小的基线网络上做一次搜索(步骤1)，然后对所有其他模型使用相同的缩放系数(步骤2)

5. Experiments

6. Discussion

为了区分我们提出的缩放方法对效率网架构的贡献，图8比较了相同效率网- b0基线网络中不同缩放方法的ImageNet性能。一般来说，所有的缩放方法都以更高的FLOPS为代价来提高精度，但我们的复合缩放方法比其他单维缩放方法可以进一步提高精度，最高可达2.5%，这表明了我们提出的复合缩放方法的重要性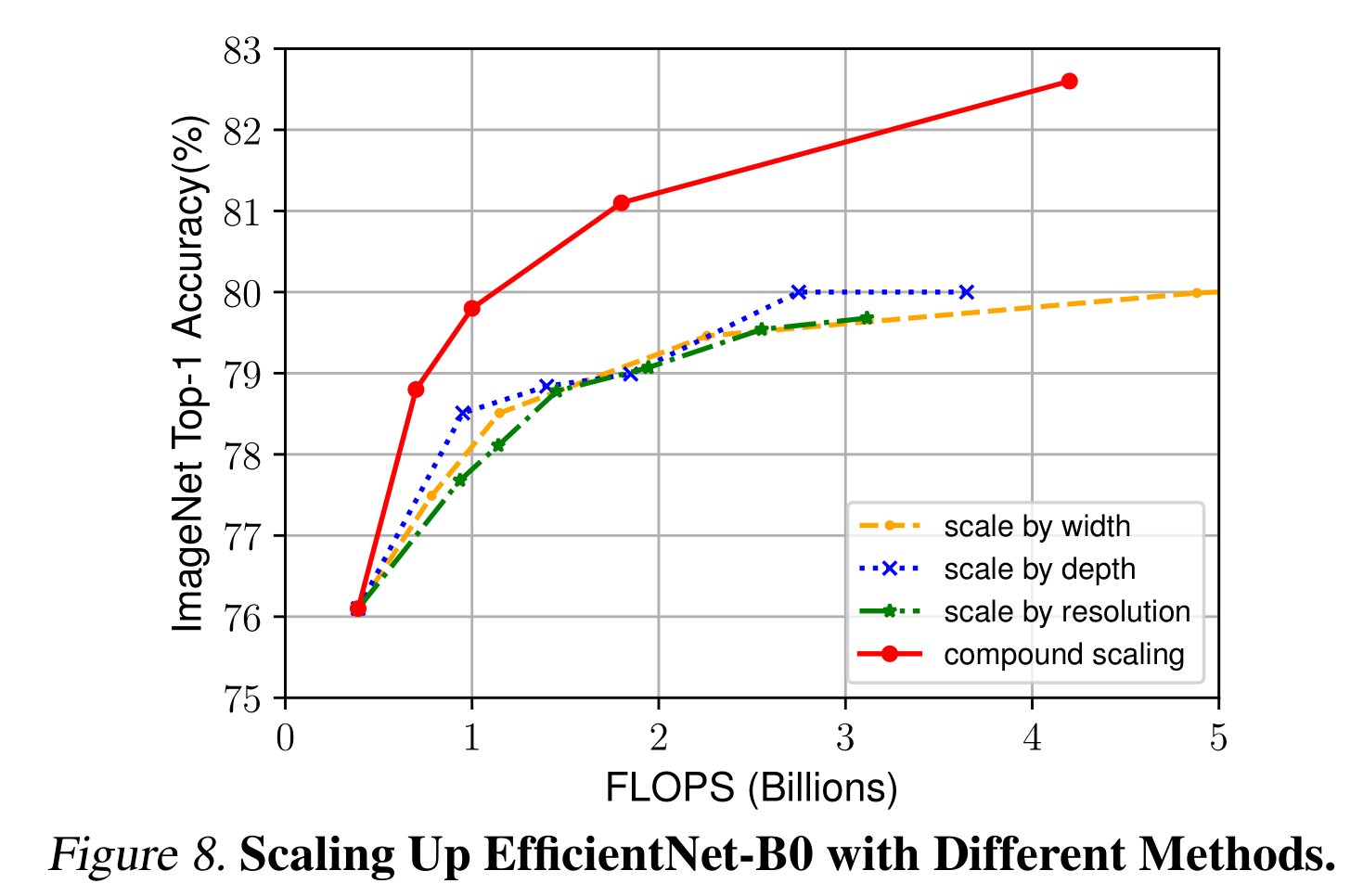
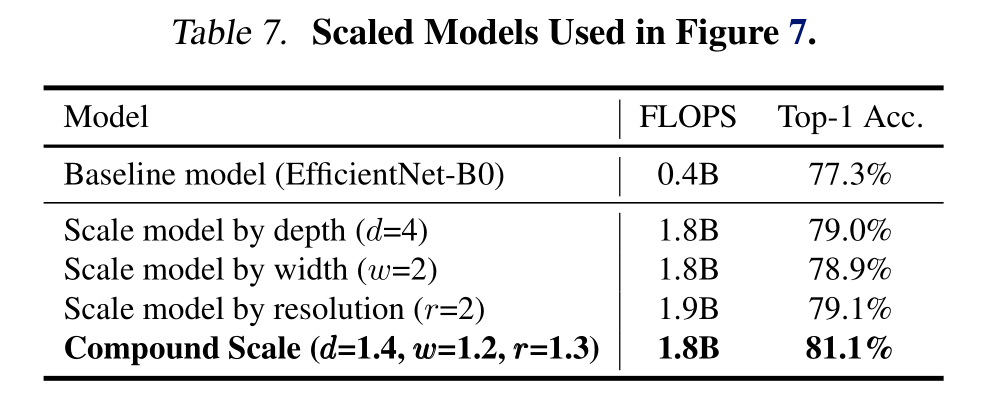
为了进一步理解为什么我们的复合缩放方法比其他方法更好，图7比较了几种不同缩放方法的代表性模型的类激活图(Zhou et al.， 2016)。所有这些模型都是从相同的基线进行缩放的，其统计数据如表7所示。图像是从ImageNet验证集中随机选取的。如图所示，复合缩放模型倾向于关注更相关的区域和更多的物体细节，而其他模型要么缺乏物体细节，要么无法捕获图像中的所有物体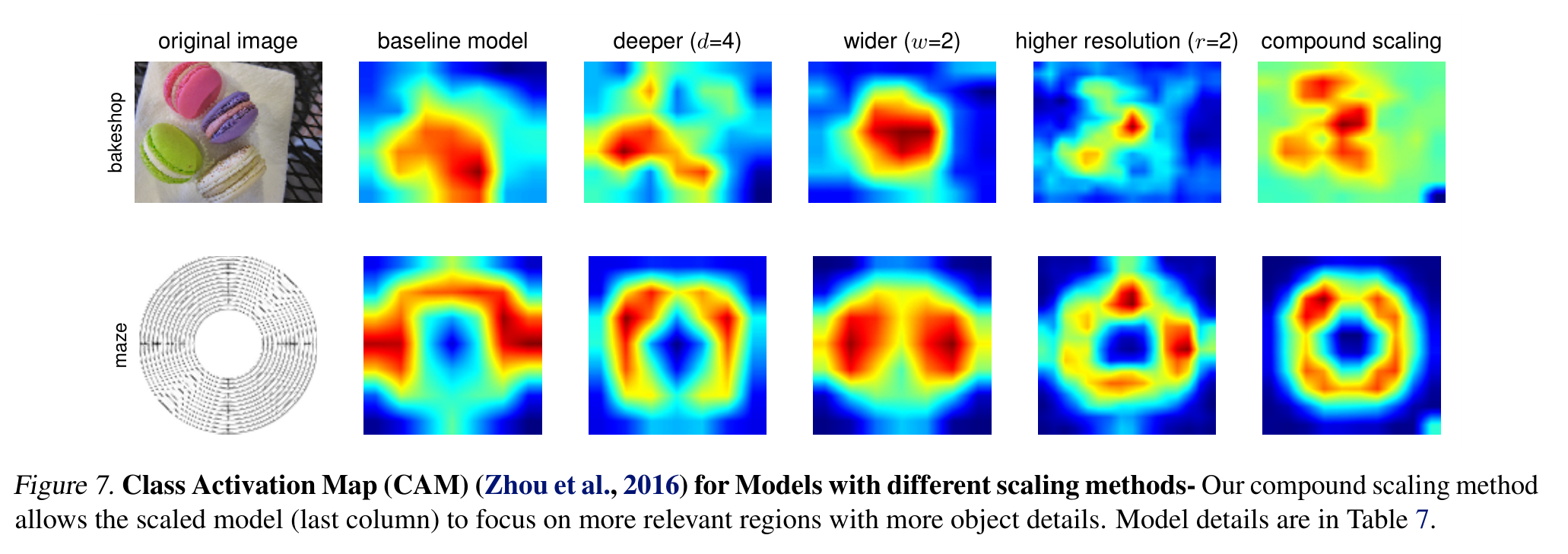

7. Conclusion

在本文中，我们系统地研究了卷积神经网络的缩放，并确定仔细平衡网络宽度，深度和分辨率是一个重要但缺失的部分，阻碍了我们更好的准确性和效率。为了解决这个问题，我们提出了一种简单而高效的复合缩放方法，该方法使我们能够以更有原则的方式轻松地将基线ConvNet扩展到任何目标资源约束，同时保持模型效率。在这种复合缩放方法的支持下，我们证明了移动尺寸的EfficientNet模型可以非常有效地缩放，在ImageNet和五种常用的迁移学习数据集上，以更少的参数和FLOPS超过了最先进的精度

这篇关于EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks（2020）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---