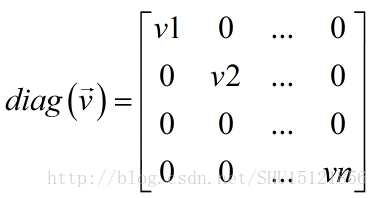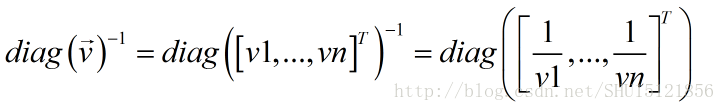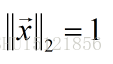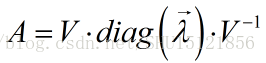本文主要是介绍【ML学习笔记】6:机器学习中的数学基础6(对角矩阵,对称矩阵,正交矩阵,特征分解),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
对角矩阵
对角矩阵不一定是个方阵,只要i≠j的位置元素值为0即可。但一般说对角矩阵,考虑的都是方阵的情况,对于方阵,那就是只有主对角线上的元素可以不为0,其它元素都是0。
主对角元从左上角到右下角的次序常常记为一个列向量:
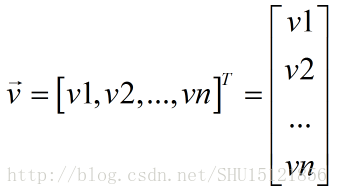
然后以它们为主对角元的对角方阵就可以记为diag(v):
对角方阵和向量的标准乘积
对角矩阵和向量的乘积比较方便,可以表示成Hadamard乘积(元素对应乘积):
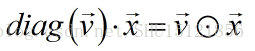
也就是把主对角元上的元素依次乘到向量的分量上去。
对角方阵求逆
对角矩阵求逆也很方便,只要把主对角线上每个元素变成其倒数就好:
对称矩阵
转置和自己相等的矩阵就是对称的,可见对称矩阵一定是个方阵,而且A[i][j]=A[j][i]。当某些不依赖参数顺序的双参数函数生成元素时,就经常会出现对称矩阵。
比如数据结构中学无向图时,邻接矩阵就是一个对称矩阵,因为i到j的权重和j到i的权重在无向图中是一样的(不依赖参数的顺序)。
单位向量e
具有单位L2范数的向量就是单位向量,也就是向量两端的欧几里徳距离等于1:
向量的正交
如果两个向量x和y的内积存在并且是0,那么这两个向量就是正交的。显然任意一个向量都会和同维度的零向量(L2范数为0的向量)正交,如果正交两个向量都不是零向量,它们的夹角就是90度。在n维的线性空间中,最多只能有n个非零向量互相正交。
向量的标准正交
如果一组单位向量互相正交,那么就称它们标准正交。
正交矩阵
行向量和列向量分别标准正交的方阵就是正交矩阵,显然单位矩阵I是一个特殊的正交矩阵。正交矩阵有这样的性质:
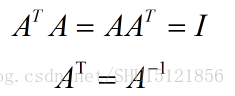
只要说明上面一条就行了,A转置的第i行,就是A的第i列,所以结果第i行第i列的元素就是两个一模一样的单位向量的内积,即是它的模1,所以整个主对角线上都是1。而对于那些i和j不相同的地方,因为相互正交,所以内积一定是0,所以除了主对角线上的其它位置的元素值都是0。
方阵的特征分解
这个在前面也了解过,特征分解可以把方阵A分解成一组特征向量和特征值。
方阵的特征向量和特征值
还是从这个经典的式子开始说:
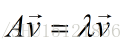
一个n阶的方阵A乘以一个n维列向量v,相当于对这个列向量缩放了λ倍,那么这个v就是方阵A的一个特征向量,而λ是对应的特征值。这个特征向量是一个列向量,其实是右特征向量,其实也有左特征向量的(是一个行向量),但不太关注它。
特征向量有多少
如果找到了方阵A的一个特征向量v,那么v缩放非0的s倍的向量都是A的特征向量:
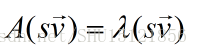
而且具有相同的特征值λ,因此特征向量如果有就有无穷多个,所以通常只考虑单位特征向量。
特征分解式
如果n阶的方阵A有n个线性无关的特征向量v1~vn,对应特征值λ1~λn,定义方阵v和列向量λ:

则方阵A的特征分解如下:
证明特征分解
这一部分书上没有,自己推了一下,总之就是能从前面那个经典的式子推出特征分解的等式是成立的就可以。
从特征值和特征向量的定义式子Av=λv开始,展开也就是:
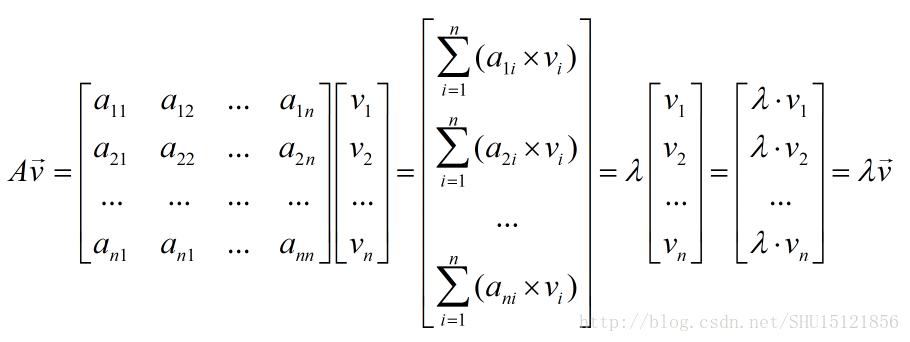
如果能找到方阵A的n个线性无关的特征向量,组成一个方阵V:

则方阵A右乘这个n个特征向量组成的方阵V,参考前面考虑的方阵A乘以特征向量v的展开式,可以得到:

(比较一下)
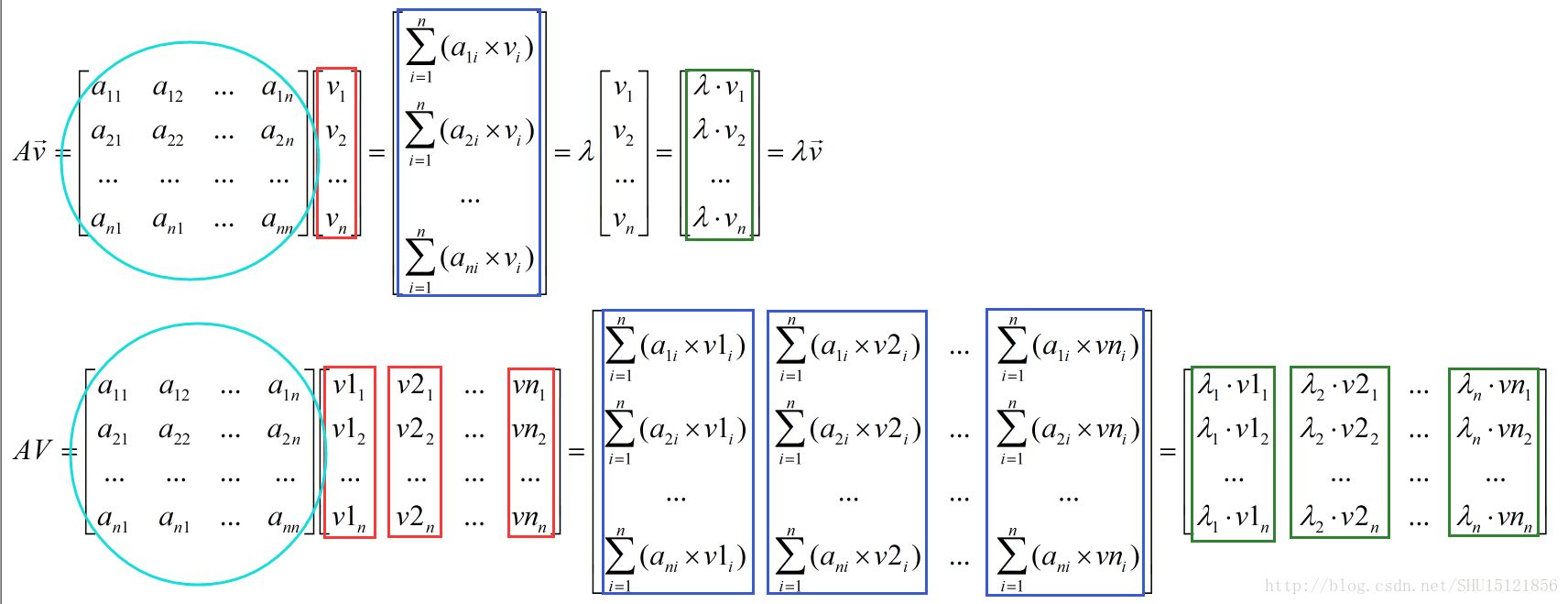
而要证的特征分解式中V和对角方阵diag(λ)的乘积:
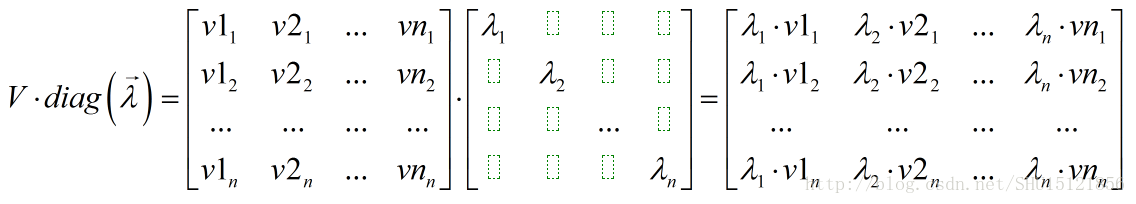
(比较一下)

所以
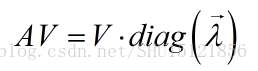
因为前面说了找的是A的n个线性无关的特征向量v组成方阵V,所以方阵V的列向量是线性无关的,非奇异矩阵可逆。两边右乘V的逆矩阵:
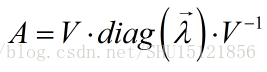
这正是方阵的特征分解式。
有关特征分解还应知道的事
有时特征分解存在,但是会涉及复数(方阵可能没有实特征值,但一定有复特征值),但每个实对称矩阵都可以分解成实特征向量和实特征值:
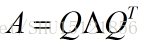
其中A是实对称矩阵,Q是A的特征向量组成的正交矩阵,Λ是特征值构成的对角矩阵(逆和转置相同),特征值Λ[i][i]对应于特征向量Q[:][i]。
具有特定特征值和特征向量的方阵,可以在特定的方向上延伸空间,比如拿前面推导中用的方阵A及其特征分解式中的特征向量组矩阵V来讲:
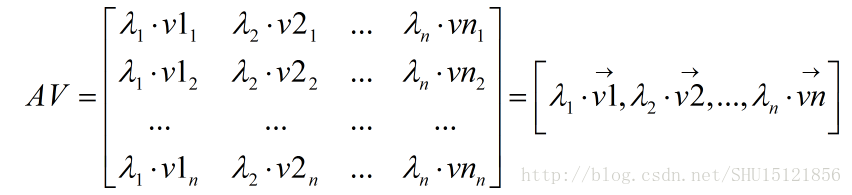
因为特征向量v1~vn都是相互正交的,所以一定可以看成n维线性空间的一组基,而用这个矩阵A去乘这个向量组构成的矩阵,也就是在这n个方向i上分别延伸之前的特征向量vi,延伸的倍数正是特征值λi。
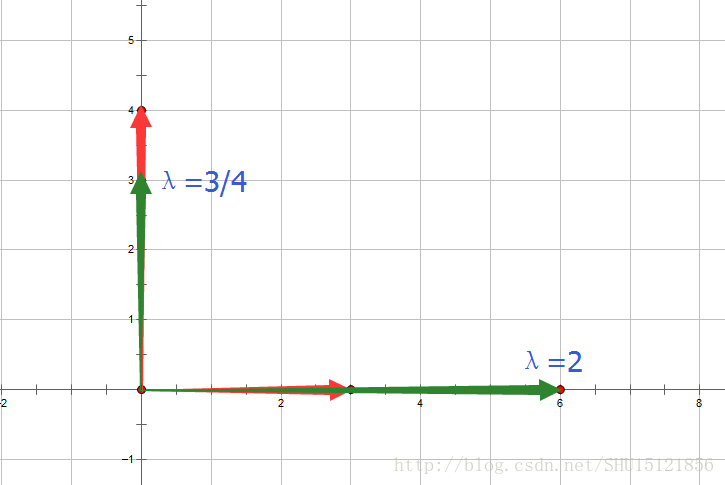
反映在空间中,正交向量的延伸(以二维为例子):
定(definite)和特征值
正定矩阵:所有特征值都是正数的方阵。
半正定矩阵:所有特征值都是非负数的方阵。
负定矩阵:所有特征值都是负数的方阵。
半负定矩阵:所有特征值都是非正数的方阵。
这篇关于【ML学习笔记】6:机器学习中的数学基础6(对角矩阵,对称矩阵,正交矩阵,特征分解)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!