对角专题
给一个二维数组,横纵坐标随机,里面数值要么是1,要么是0,统计对角是1的个数
问题:给一个二维数组,横纵坐标随机,里面数值要么是1,要么是0,统计对角是1的个数? 解析 : 首先说一下,怎样的算对角,框成一个矩形是1的就是对角,四点在直线上的值为1组成矩形就算对角。如下图,框起来的都算对角。统计它里面对角的个数?怎么算呢? 1. 如果要是对角,肯定一开始那个值为1,它在数组里面的坐标是i,j,即a[i][j] =1。 2.还要计算其他三个点是1,就需要在i,j的
对角矩阵的性质(diagonal matrix)
对角矩阵(英语:diagonal matrix)是一个主对角线之外的元素皆为0的矩阵。对角线上的元素可以为0或其他值。因此n行n列的矩阵{\displaystyle \mathbf {D} } = (di,j)若符合以下的性质: {\displaystyle d_{i,j}=0{\mbox{ if }}i\neq j\qquad \forall i,j\in \{1,2,\ldots ,n\
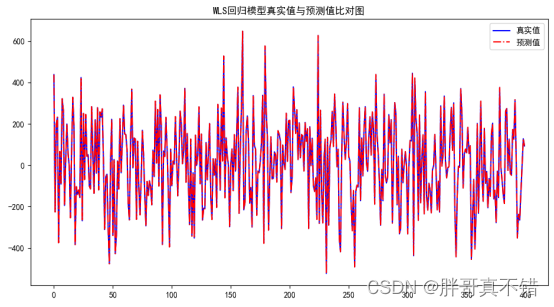
Python实现对角但非同一性协方差结构回归模型(WLS算法)项目实战
说明:这是一个机器学习实战项目(附带数据+代码+文档+视频讲解),如需数据+代码+文档+视频讲解可以直接到文章最后获取。 1.项目背景 WLS回归分析是一种常用的回归分析方法,通过对数据进行加权处理,可以更准确地评估模型参数。 本项目通过WLS回归算法来构建对角但非同一性协方差结构回归模型。 2.数据获取 本次建模数据来源于网络(本项目撰写人整理而成),数据项统计如下: 编号
对角矩阵,投影矩阵,三角矩阵的特征值性质
目录 一. 引入 二. 对角矩阵 2.1 对角矩阵的特征值与特征向量 2.2 小结 三. 投影矩阵 3.1 投影矩阵的特征值与特征向量 3.2 小结 四. 三角矩阵 4.1 三角矩阵的特征值与特征向量 4.2 小结 五. 矩阵的迹,行列式,特征值之间的关系 5.1 特征值与求解Ax=b 5.2 特征值的求和与求积 一. 引入 对于如下的微分方程: 其解肯
009 matlab语言实现一点到对角的路径PART2--优化与升级
之前一篇blog已经说明了最基本的情况,这里不再罪赘述(008 matlab语言实现一点到对角的路径PART1) 最近,对这个问题做了一些改进与优化。 1、改进:增加了不可到达点 其实这个还是很容易实现得,只需要检查路径中有没有这样不能到达的点,然后这样的路径不画出来就行了,改进部分代码如下: for j=1:length(Paths(1,:))x=x+Paths(2,
008 matlab语言实现一点到对角的路径PART1
昨天,同学在群里发了一个数据结构及算法方面的题目(如下图),由于最近在学习MATLAB,所以突发奇想,能不能借助MATLAB强大的绘图功能把所有路径画出来。经过几次失败的探索,终于算是完整的实现了最初的想法,收获也是相当之多。 这里我并没有一开始就考虑有特殊P点的情况,而是研究从一个顶点到对角顶点的所有路径(考虑P点的情况将在以后给出)。 首先,对这个问题做一些数学分析(感谢高中的
2019-04-29:对称矩阵:遍历输出矩阵,求矩阵的正对角和,反对角和
#encoding=utf-8"""用嵌套列表的方式,遍历输出一个矩阵"""#方法一def traversMatrix(matrix):for i in matrix:for j in i:print(j,end=" ")print()matrix=[[1,2,3],[4,5,6],[7,8,9]]print(traversMatrix(matrix))#方法二def traversM
【ML学习笔记】6:机器学习中的数学基础6(对角矩阵,对称矩阵,正交矩阵,特征分解)
对角矩阵 对角矩阵不一定是个方阵,只要i≠j的位置元素值为0即可。但一般说对角矩阵,考虑的都是方阵的情况,对于方阵,那就是只有主对角线上的元素可以不为0,其它元素都是0。 主对角元从左上角到右下角的次序常常记为一个列向量: 然后以它们为主对角元的对角方阵就可以记为diag(v): 对角方阵和向量的标准乘积 对角矩阵和向量的乘积比较方便,可以表示成Hadamard乘积(元素对应乘积
对角占优阵的行列式大于零的证明
M = ( a b c d ) 满 足 : a > ∣ b ∣ , d > ∣ c ∣ M=\left( \begin{array} { l l } { a } & { b } \\ { c } & { d} \end{array}\right)\\ 满足:a>|b|,d>|c| M=(acbd)满足:a>∣b∣,d>∣c∣ 另 M ( t ) = ( a b ∗ t c ∗ t d )