本文主要是介绍第三章-数据存储<Foundations of computer science>(Part Three ),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
例3.17
在十进制系统中,假设我们使用定点表示法,小数点右边有6位数字,小数点左边有10位数字,总共16位数字。在这个系统中,如果我们试图表示一个十进制数,如236154302345.00,那么实数的准确性就会丢失。系统将号码存储为
6154302345.00:积分部分比应有的要小得多
具有非常大的整数部分或非常小的小数部分的实数不应存储在定点表示中。
浮点表示法
保持准确性或精度的解决方案是使用浮点表示。
这种表示允许小数点浮动:小数点的左边或右边可以有不同的位数。使用这种方法可以存储的实数范围大大增加:具有大整数部分或小小数部分的数字可以存储在内存中。在浮点表示(十进制或二进制)中,一个数字由三个部分组成,如图3.10所示。
图3.10实数的三部分浮点表示法

第一部分是符号,或正或负。第二部分展示了小数点应该向左或向右移动多少位才能形成实际的数字。第三部分是一个定点表示,其中小数点的位置是固定的。
一个数字的浮点表示由三个部分组成:符号、移位符和定点数。
在科学中,浮点表示法用于表示非常小或非常大的十进制数。在这种称为scientif ic表示法的表示中,定点部分在小数点的左边只有一位数字,移位器是10的幂。
例3.18
下面显示了科学记数法(浮点表示)中的十进制数7 425 000 000 000 000 000 000 000.00:
解决方案
Actual number → + 7 425 000 000 000 000 000 000.00
Scientific notation → + 7.425 × 1021
这三个部分分别是符号(+),移位器(21)和定点部分(7.425)。
注意,移位器是指数。我们可以很容易地看到这样做的好处。即使我们只是想把数字写在一张纸上,科学记数法也更短,占用的空间更小。该表示法使用了浮点数的概念,因为小数点的位置(在示例中靠近右端)向左移动了21位,以使数字的定点部分变为定点部分。一些编程语言和计算器显示的数字是+7.425E21,因为基数10是可以理解的,不需要提及。
例3.19
以科学记数法显示数字-0.0000000000000232。
解决方案
我们使用与前面示例相同的方法—将小数点移到数字2后面,如下所示:
Actual number → - 0.0000000000000232
Scientific notation → - 2.32 × 10−14
请注意,这里的指数是负的,因为2.32中的小数点需要向左移动(14位)才能形成原始数字。同样,我们可以说,在这种符号中,数字由三部分组成:符号(-),实数(2.32)和负整数(-14)。一些编程语言和计算器将其表示为
-2.32 e-14。
类似的方法也被用于表示非常大或非常小的数字
(包括整数和实数)二进制,存储在计算机中。
例3.20
以浮点格式显示数字(1010010000000000000000000000000000000.00)2。
解决方案
我们使用同样的方法,在小数点的左边只保留一位数字
Actual number → + (101001000000000000000000000000000.00)2
Scientific notation → + 1.01001 × 232 :
请注意,我们不必担心最右边的1右边的所有0,因为当我们使用实数(1.01001)2时,它们并不重要。指数显示为32,但它实际上以二进制形式存储在计算机中,我们很快就会看到。我们也将符号表示为正,但它将被存储为1位。
例3.21
以浮点格式显示数字-(0.00000000000000000000000101)2。
解决方案
我们用同样的方法,在小数点左边只保留一个非零的数字
Actual number → - (0.00000000000000000000000101)2
Scientific notation → - 1.01 × 2-24
请注意,指数在计算机中以负二进制形式存储。
归一化
为了使表示的固定部分一致,科学方法(用于十进制)和浮点方法(用于二进制)在小数点的左边只使用一个非零数字。这叫做归一化。在十进制系统中,这个数字可以是1到9,而在二进制系统中,它只能是0或1。其中,d为非零数字,x为数字,y为0或1:
Decimal ± d.xxxxxxxxxxxxxx Note: d is 1 to 9 and each x is 0 to 9
Binary ± 1.yyyyyyyyyyyyyy Note: each y is 0 or 1
符号,指数和尾数
二进制数规范化后,只存储有关该数的三条信息:符号、指数和尾数(小数点右侧的位)。例如,+1000111.0101变成:
Sign Exponent Mantissa
+ 26 × 1.0001110101
1 6 0001110101
注意,定点部分左边的点和位1不是存储的——它们是隐式的。
标志
数字的符号可以用1位(0或1)来存储。
指数
指数(2的幂)定义小数点的移位。注意,幂可以是负的也可以是正的。过剩表示(稍后讨论)是用于存储指数的方法。
尾数
尾数是小数点右边的二进制整数。它定义了数字的精度。尾数以定点表示法存储。如果我们把尾数和符号放在一起考虑,我们可以说这个组合被存储为符号和大小格式的整数,但是,我们需要记住,它不是整数——它是像整数一样存储的小数部分。我们强调这一点是因为在尾音中
如果在数字的右侧插入额外的0,则值不会改变,而在实整数中,如果在数字的左侧插入额外的0,则值不会改变。
尾数是一个小数部分,与符号一起,被视为存储在符号和大小表示中的整数。
超额系统
尾数可以存储为无符号整数。指数是表示小数点应该向左或向右移动多少位的幂,它是一个有符号数。
虽然这可以使用2的补码表示来存储,但这里使用了一种称为Excess系统的新表示。在Excess系统中,正整数和负整数都存储为无符号整数。为了表示正整数或负整数,在每个数字上加一个正整数(称为偏置),使它们均匀地移到非负侧。这个偏置的值是2m-1 -1,其中m是存储指数的内存位置的大小。
例3.22
我们可以在4位分配的数字系统中表示16个整数。使用一个位置表示0,并将其他15个位置分开(不完全相等),我们可以表示范围为-7到8的整数,如图3.11所示。通过给这个范围内的每个整数加7个单位,我们可以在不改变整数彼此的相对位置的情况下,将所有的整数均匀地向右平移,使它们都为正,如图所示。新系统被称为Excess-7,或偏置值为7的偏置表示。

与转换之前相比,这种新表示的优势在于,过剩系统中的所有整数都是正的,所以当我们对整数进行比较或操作时,我们不需要关心符号。对于4位分配,偏差是24-1 -1 = 7,正如我们所期望的那样。
IEEE标准
电气和电子工程师协会(IEEE)为存储浮点数定义了几个标准。我们在这里讨论两个最常见的,精度和双精度。这些格式如图3.12所示。方框上方的数字是每个字段的位数。
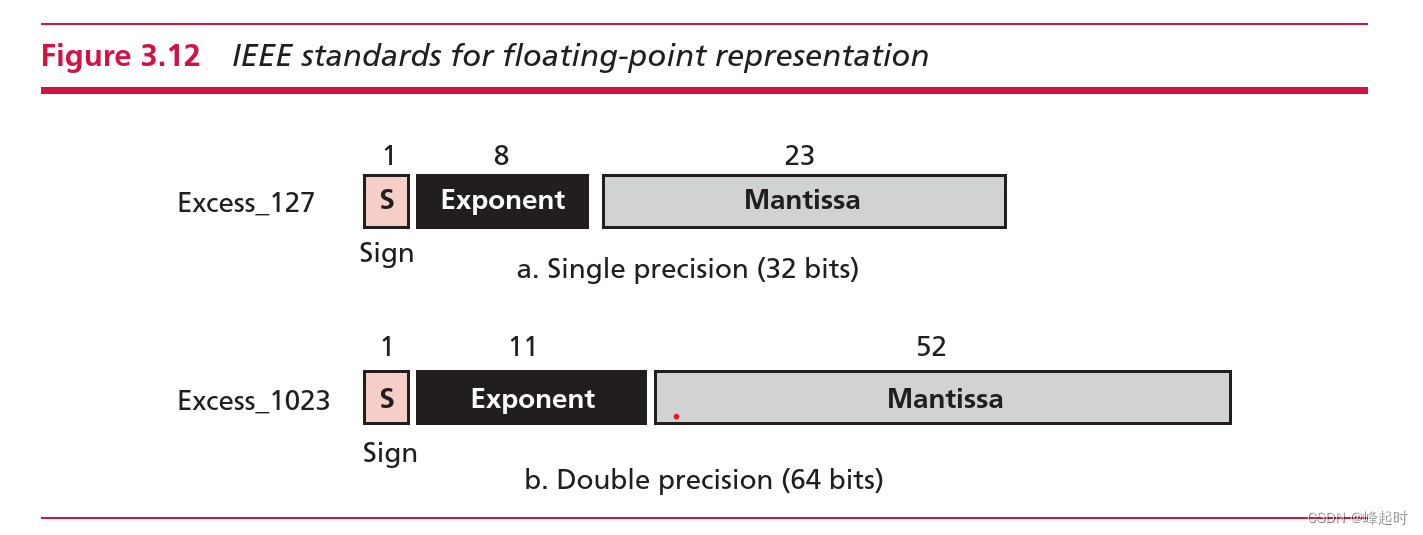
单精度格式总共使用32位来存储浮点表示的实数。符号占用1位(0表示正,1表示负),指数占用8位(使用127的偏置),尾数占用23位(无符号数)。这个标准有时被称为Excess_127,因为偏差是127。
双精度格式总共使用64位来存储浮点表示的实数。符号占用1位,指数占用11位(使用偏置)
1023),尾数使用52位。该标准有时被称为Excess_1023,因为偏差为1023。表3.2总结了两个标准的规格。
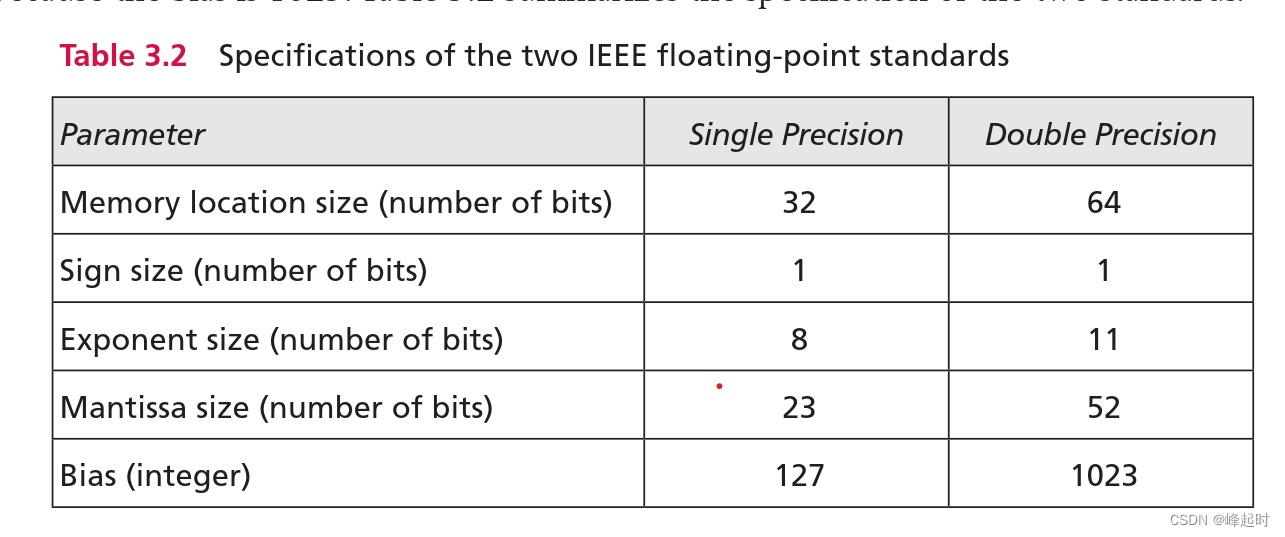
存储IEEE标准浮点数
实数可以用IEEE标准浮点格式之一存储,具体步骤参见图3.12:
将符号存储在S(0或1)中
改变数字为二进制。
正常化。
发现E和M的值
把S、E、M连接起来
例3.23
显示十进制数5.75的Excess_127(单精度)表示形式。
解
a,符号是正的,所以S = 0。
b.十进制到二进制转换:5.75 =(101.11)2。
c.归一化:(101.11)2 = (1.0111)2 × 22。
d. E = 2 + 127 = 129 = (10000001)2, M = 0111。我们需要在右边加19个0
M变成23位。
e.演示如下:
S E M
0 10000001 01110000000000000000000
该数字在计算机中存储为01000000101110000000000000000000。
例3.24
显示十进制数-161.875的Excess_127(单精度)表示形式。
解
a,符号是负的,所以S = 1。
b.十进制到二进制的转换:161.875 = (10100001.111)
c.归一化:(10100001.111)2 = (1.0100001111)2 × 27。
d. E = 7 + 127 = 134 = (10000110)2, M =(0100001111)2。
e。表示:
S E M
1 10000110 01000011110000000000000
这篇关于第三章-数据存储<Foundations of computer science>(Part Three )的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





