考研数学线上笔记（六）：凯哥微分方程、多元微分、无穷级数概念选择题系列课程

2023-12-06 08:30
文章标签 线上 笔记 概念 系列 考研 数学 微分方程 课程 选择题 无穷 凯哥 级数 多元 微分

本文主要是介绍考研数学线上笔记（六）：凯哥微分方程、多元微分、无穷级数概念选择题系列课程，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

  • 微分方程
    • 一阶线性微分方程
      • 一阶微分方程可以用“齐次通解+非齐次特解”；非齐次的两个解的差乘上C即为齐次的通解
      • 任意常数个数和阶数相同-->非齐次前的系数之和满足1（非齐次）或0（齐次）-->解的组合是非齐次或齐次的解
      • 上述结论的前提是解不成比例（即线性无关）
    • 高阶齐次线性的解法---利用e^λx^特征根是λ求出等号左边，非齐次的特解代入求出等号右边
      • 已知方程，求通解
      • 已知通解，反求方程
    • 非齐次的两个解的差乘上C即为齐次的通解，齐次的通解+另一个非齐次的特解即为该
    • 二阶非齐次的特解求解
    • 两边取极限、两边取积分
    • 几个杂题
  • 多元函数微分学
    • 概念性质
      • 几个概念的强弱关系
      • 利用定义进行全微分（偏导）计算，选择题可以把x、y的系数的相反数作为偏导数直接秒
      • 二阶混合偏导数（即先y后x与先x后y）相等
    • 无条件极值
    • 条件极值（拉格朗日乘数法）
    • 脱帽法的应用
    • 隐函数存在定理
  • 常数项级数
    • 常见结论
    • 比较判别法适用于正项级数（不变号级数）
    • a~n~+a~n+1~、a~2n-1~+a~2n~算是加括号；a~2n-1~-a~2n~加括号实际进行了一次交错，可能把本身交错变回去
    • 偶数次方同时进行了正数化和提阶，无法判断敛散性
    • 加了括号收敛的级数，若为正项级数，则原单项的级数也收敛
    • 条件收料即本身收敛，加绝对值后发散
    • 已知敛散性推不出阶数，阶数也不可以判断敛散性；莱布尼茨判别法需要同时满足递减和趋于0
    • 正数项级数，单纯是1/n的高阶无穷小，仍然推不出收敛，只有当就是1/n^p^，p>1才能断定收敛；
    • 1/n无法作为判别级数收敛的依据；1/nln(n)是发散的（积分判别法），常作为反例；ln(n)/n^p^，只要p>1就收敛
    • 不要把数列的平方和级数的平方搞混
  • 幂级数
    • 常用展开式
    • 利用展开式求函数
    • 假装先积后导再直接套公式出结果
    • 常数项级数可以转化为幂级数和函数在某点的取值

微分方程

一阶线性微分方程

一阶微分方程可以用“齐次通解+非齐次特解”；非齐次的两个解的差乘上C即为齐次的通解

在这里插入图片描述

任意常数个数和阶数相同–>非齐次前的系数之和满足1（非齐次）或0（齐次）–>解的组合是非齐次或齐次的解

上述结论的前提是解不成比例（即线性无关）

在这里插入图片描述

高阶齐次线性的解法—利用eλx特征根是λ求出等号左边，非齐次的特解代入求出等号右边

在这里插入图片描述

已知方程，求通解

在这里插入图片描述

已知通解，反求方程

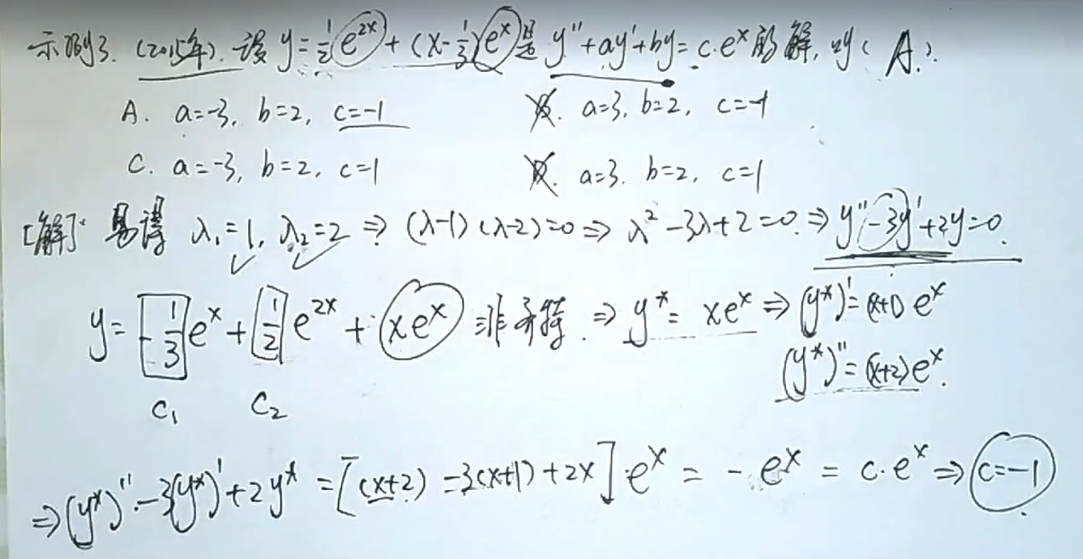
在这里插入图片描述

在这里插入图片描述

非齐次的两个解的差乘上C即为齐次的通解，齐次的通解+另一个非齐次的特解即为该

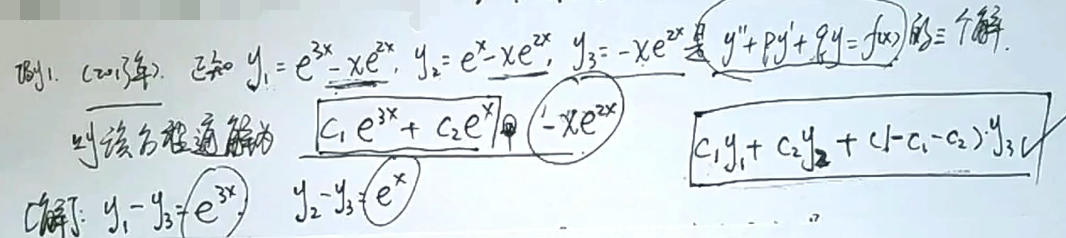
在这里插入图片描述

二阶非齐次的特解求解

在这里插入图片描述

两边取极限、两边取积分

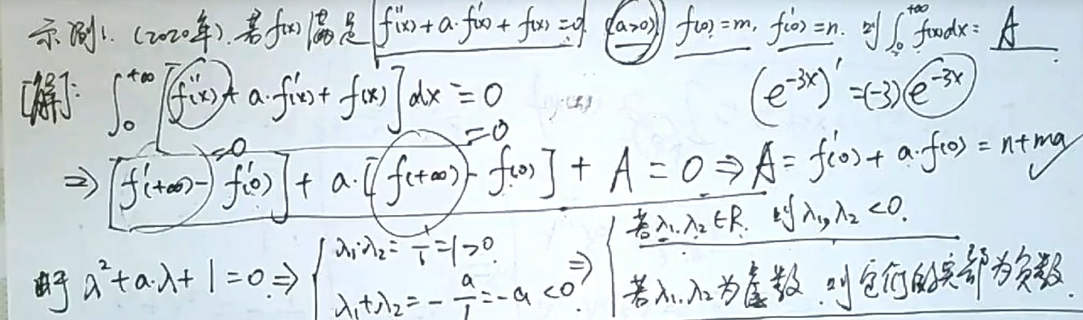
在这里插入图片描述
在这里插入图片描述

几个杂题

在这里插入图片描述

在这里插入图片描述

多元函数微分学

概念性质

几个概念的强弱关系

一阶偏导连续最强，可微次之
单纯的可偏导推不出任何结论，可偏导和连续没有任何关系

在这里插入图片描述
一阶偏导要求是二元极限等于该点的偏导值

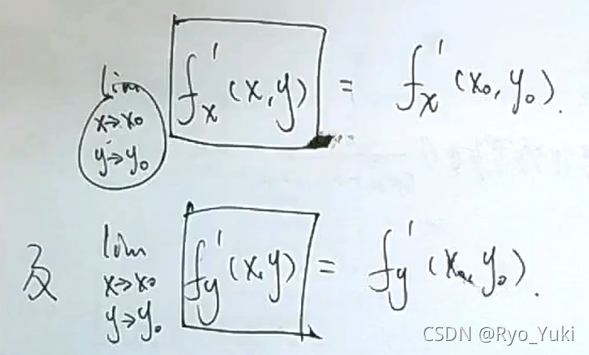
在这里插入图片描述

AB单纯的偏导无法推连续和极限，C单纯的偏导推不出可微，需要加可微的条件才成立
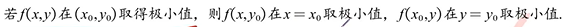
在这里插入图片描述
在这里插入图片描述
C选项
在这里插入图片描述

利用定义进行全微分（偏导）计算，选择题可以把x、y的系数的相反数作为偏导数直接秒

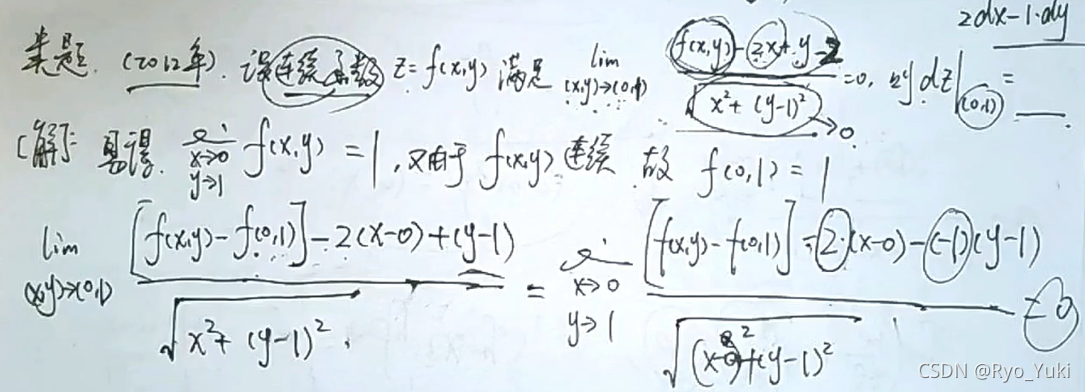
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

二阶混合偏导数（即先y后x与先x后y）相等

在这里插入图片描述

无条件极值

A是x的二阶偏导，C是y的二阶偏导，B是先x后y的二阶偏导

在这里插入图片描述

在这里插入图片描述

条件极值（拉格朗日乘数法）

在这里插入图片描述

脱帽法的应用

在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

隐函数存在定理

在这里插入图片描述

常数项级数

常见结论

收+收=收、收+发=发、发+发=？
正项级数大收敛推小收敛，小发散推大发散；
加绝对值，提高发散性；
改为交错级数，提高收敛性；
本身就是交错级数再交错、交错级数相乘，提高发散性；
提高一般项的阶数，提高收敛性；
非正项级数加括号，提高收敛性，正项级数加了也白加；（a2n+a2n+1算加括号，减号、an+an+1不算）
交错和提阶同时进行时，无法判断敛散性；
进行偶数次方时，同时进行了正数化和提阶，无法判断敛散性；
在这里插入图片描述
在这里插入图片描述

反例

在这里插入图片描述

比较判别法适用于正项级数（不变号级数）

在这里插入图片描述

an+an+1、a2n-1+a2n算是加括号；a2n-1-a2n加括号实际进行了一次交错，可能把本身交错变回去

在这里插入图片描述

在这里插入图片描述

偶数次方同时进行了正数化和提阶，无法判断敛散性

在这里插入图片描述

加了括号收敛的级数，若为正项级数，则原单项的级数也收敛

在这里插入图片描述

条件收料即本身收敛，加绝对值后发散

在这里插入图片描述

已知敛散性推不出阶数，阶数也不可以判断敛散性；莱布尼茨判别法需要同时满足递减和趋于0

在这里插入图片描述

正数项级数，单纯是1/n的高阶无穷小，仍然推不出收敛，只有当就是1/np，p>1才能断定收敛；

在这里插入图片描述

1/n无法作为判别级数收敛的依据；1/nln(n)是发散的（积分判别法），常作为反例；ln(n)/np，只要p>1就收敛

在这里插入图片描述

不要把数列的平方和级数的平方搞混

在这里插入图片描述

幂级数

常用展开式

在这里插入图片描述

利用展开式求函数

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

假装先积后导再直接套公式出结果

在这里插入图片描述

常数项级数可以转化为幂级数和函数在某点的取值

在这里插入图片描述

这篇关于考研数学线上笔记（六）：凯哥微分方程、多元微分、无穷级数概念选择题系列课程的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/461148。

相关文章

Spring Security 从入门到进阶系列教程

Spring Security 从入门到进阶系列教程

Spring Security 入门系列 《保护 Web 应用的安全》 《Spring-Security-入门（一）：登录与退出》 《Spring-Security-入门（二）：基于数据库验证》 《Spring-Security-入门（三）：密码加密》 《Spring-Security-入门（四）：自定义-Filter》 《Spring-Security-入门（五）：在 Sprin
阅读更多...
如何解决线上平台抽佣高 线下门店客流少的痛点！

如何解决线上平台抽佣高 线下门店客流少的痛点！

目前，许多传统零售店铺正遭遇客源下降的难题。尽管广告推广能带来一定的客流，但其费用昂贵。鉴于此，众多零售商纷纷选择加入像美团、饿了么和抖音这样的大型在线平台，但这些平台的高佣金率导致了利润的大幅缩水。在这样的市场环境下，商家之间的合作网络逐渐成为一种有效的解决方案，通过资源和客户基础的共享，实现共同的利益增长。 以最近在上海兴起的一个跨行业合作平台为例，该平台融合了环保消费积分系统，在短
阅读更多...
科研绘图系列：R语言扩展物种堆积图（Extended Stacked Barplot）

科研绘图系列：R语言扩展物种堆积图（Extended Stacked Barplot）

介绍 R语言的扩展物种堆积图是一种数据可视化工具，它不仅展示了物种的堆积结果，还整合了不同样本分组之间的差异性分析结果。这种图形表示方法能够直观地比较不同物种在各个分组中的显著性差异，为研究者提供了一种有效的数据解读方式。 加载R包 knitr::opts_chunk$set(warning = F, message = F)library(tidyverse)library(phyl
阅读更多...
uva 10014 Simple calculations（数学推导）

uva 10014 Simple calculations（数学推导）

直接按照题意来推导最后的结果就行了。 开始的时候只做到了第一个推导，第二次没有继续下去。 代码： #include<stdio.h>int main(){int T, n, i;double a, aa, sum, temp, ans;scanf("%d", &T);while(T--){scanf("%d", &n);scanf("%lf", &first);scanf
阅读更多...
uva 10025 The ? 1 ? 2 ? ... ? n = k problem（数学）

uva 10025 The ? 1 ? 2 ? ... ? n = k problem（数学）

题意是    ?  1  ?  2  ?  ...  ?  n = k 式子中给k，? 处可以填 + 也可以填 - ，问最小满足条件的n。 e.g k = 12  - 1 + 2 + 3 + 4 + 5 + 6 - 7 = 12 with n = 7。 先给证明，令 S（n） = 1 + 2 + 3 + 4 + 5 + .... + n 暴搜n，搜出当 S（n） >=
阅读更多...
uva 11044 Searching for Nessy（小学数学）

uva 11044 Searching for Nessy（小学数学）

题意是给出一个n*m的格子，求出里面有多少个不重合的九宫格。 (rows / 3) * (columns / 3) K.o 代码： #include <stdio.h>int main(){int ncase;scanf("%d", &ncase);while (ncase--){int rows, columns;scanf("%d%d", &rows, &col
阅读更多...
【生成模型系列（初级）】嵌入（Embedding）方程——自然语言处理的数学灵魂【通俗理解】

【生成模型系列（初级）】嵌入（Embedding）方程——自然语言处理的数学灵魂【通俗理解】

【通俗理解】嵌入（Embedding）方程——自然语言处理的数学灵魂 关键词提炼 #嵌入方程 #自然语言处理 #词向量 #机器学习 #神经网络 #向量空间模型 #Siri #Google翻译 #AlexNet 第一节：嵌入方程的类比与核心概念【尽可能通俗】 嵌入方程可以被看作是自然语言处理中的“翻译机”，它将文本中的单词或短语转换成计算机能够理解的数学形式，即向量。 正如翻译机将一种语言
阅读更多...
【学习笔记】 陈强-机器学习-Python-Ch15 人工神经网络（1）sklearn

【学习笔记】 陈强-机器学习-Python-Ch15 人工神经网络（1）sklearn

系列文章目录 监督学习：参数方法 【学习笔记】 陈强-机器学习-Python-Ch4 线性回归 【学习笔记】 陈强-机器学习-Python-Ch5 逻辑回归 【课后题练习】 陈强-机器学习-Python-Ch5 逻辑回归（SAheart.csv） 【学习笔记】 陈强-机器学习-Python-Ch6 多项逻辑回归 【学习笔记 及 课后题练习】 陈强-机器学习-Python-Ch7 判别分析 【学
阅读更多...
系统架构师考试学习笔记第三篇——架构设计高级知识（20）通信系统架构设计理论与实践

系统架构师考试学习笔记第三篇——架构设计高级知识（20）通信系统架构设计理论与实践

本章知识考点：         第20课时主要学习通信系统架构设计的理论和工作中的实践。根据新版考试大纲,本课时知识点会涉及案例分析题(25分),而在历年考试中,案例题对该部分内容的考查并不多,虽在综合知识选择题目中经常考查,但分值也不高。本课时内容侧重于对知识点的记忆和理解,按照以往的出题规律,通信系统架构设计基础知识点多来源于教材内的基础网络设备、网络架构和教材外最新时事热点技术。本课时知识
阅读更多...
flume系列之：查看flume系统日志、查看统计flume日志类型、查看flume日志

flume系列之：查看flume系统日志、查看统计flume日志类型、查看flume日志

遍历指定目录下多个文件查找指定内容 服务器系统日志会记录flume相关日志 cat /var/log/messages |grep -i oom 查找系统日志中关于flume的指定日志 import osdef search_string_in_files(directory, search_string):count = 0
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2