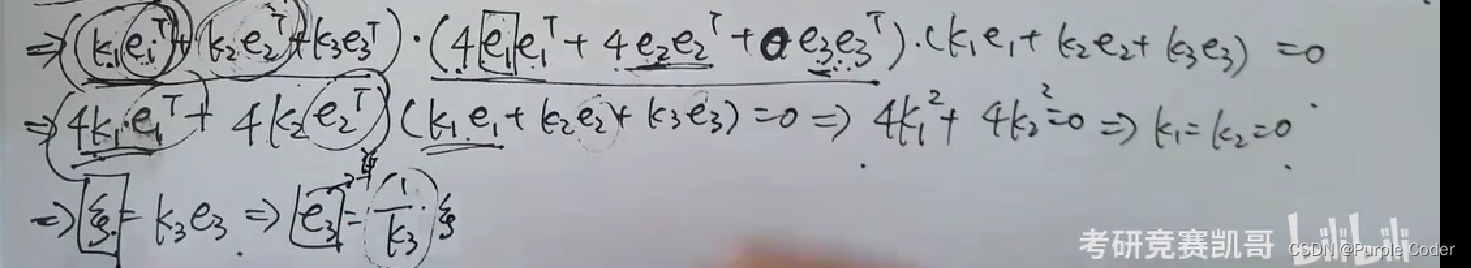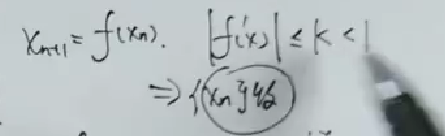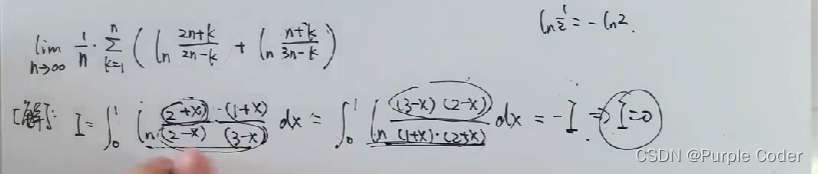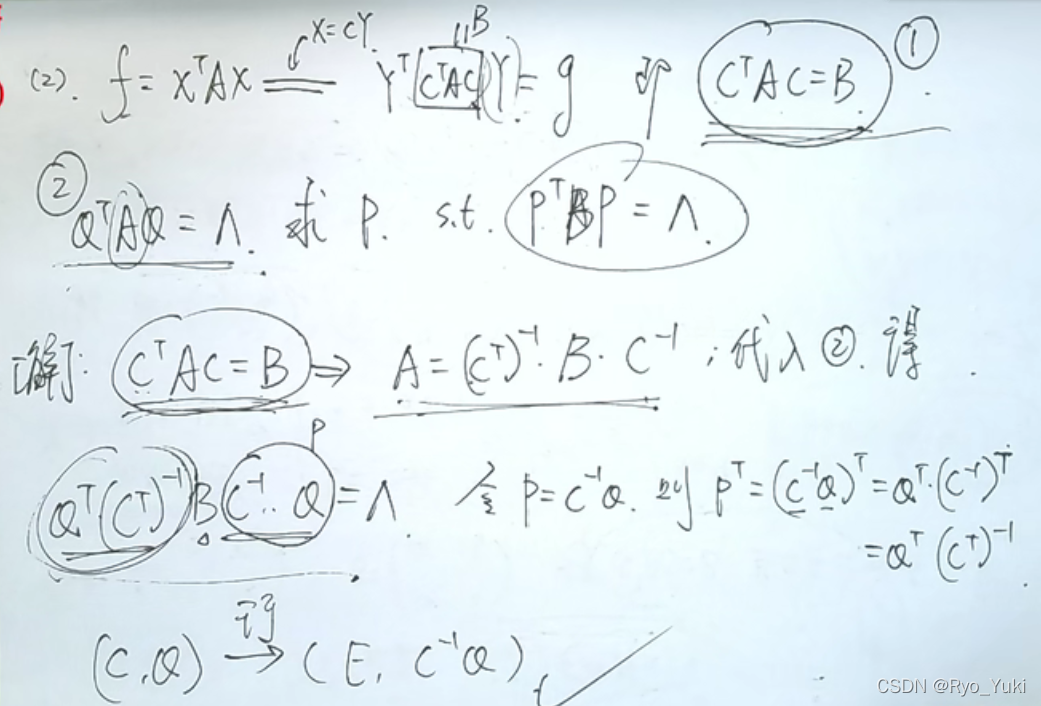凯哥Java的社区地址：http://t.csdnimg.cn/DQW88 欢迎大家加入

【ps:本文为系列教程，在文章末尾会有本系列其他教程传送门】 在前两节学习中我们知道了freemark的hello Word 以及freemark的部分数据类型。 本节我们继续学习freemark的流程控制语句以及list、map对象数据怎么获取。 本节主要内容： 1：流程控制语句 2：从list中获取数据 3：从map中获取数据 4：list和map结合使用从中获取数据 5：function的

目录 微分方程一阶线性微分方程一阶微分方程可以用“齐次通解+非齐次特解”；非齐次的两个解的差乘上C即为齐次的通解任意常数个数和阶数相同-->非齐次前的系数之和满足1（非齐次）或0（齐次）-->解的组合是非齐次或齐次的解上述结论的前提是解不成比例（即线性无关） 高阶齐次线性的解法---利用e^λx^特征根是λ求出等号左边，非齐次的特解代入求出等号右边已知方程，求通解已知通解，反求方程 非齐次的

套路一：妙用添项减项，凑出需要的结构 另解：逆用等价 套路二：见到幂指函数，一般要取指对数 套路三：当等价无穷小的精度不够时，通常采用泰勒展开求极限 套路四：无分母时的泰勒展开 套路五：求参数的值，使得无穷小的阶数尽可能的高 套路七：已知一个极限，求另一个极限 脱帽法 套路十：复合函数的泰勒展开 例题2

求互相正交的向量 求参数C   对称矩阵和不对称矩阵永远不能合同 合同对角化 模板 目的   配方+线性方程组 一般变换：合同 正交变换： 相似

特殊值法 f（x） =  x 对称矩阵和不对称矩阵永远不能合同 圆柱侧面面积为  2 * Pi  *  r  *  h  投影要有面积 这个要注意前侧+后侧（投影） 侧面面积不用直接算，有对应关系  dxdy 上下不对称。所以第二类曲面积分，偶0奇倍                  x可以变，但是结果为0，则

格林公式（挖洞又补线） 减去顺时针的  =  加上逆时针的 斯托克斯方程    我tm弄不死你

目录 特征值与特征向量逆用矩阵乘法和相似求特征值秩为1的矩阵，特征值为n-1个0和一个tr(A)（主对角线之和）每行元素之和相同，特征值为该和；特征值也满足f(A)=0迹是对角线之和，也是特征值之和；f(A)=0求出的是所有特征值的取值，但不是所有特征值特征值相乘为行列式的值伴随的迹是对角线位置的代数余子式之和特征值：A^*^=|A|/λ特征值对应一个特征向量；但特征值和特征向量之间没有倍数