本文主要是介绍二次型(感谢凯哥),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!






求互相正交的向量

求参数C

对称矩阵和不对称矩阵永远不能合同
合同对角化

模板
目的


配方+线性方程组
一般变换:合同
正交变换: 相似







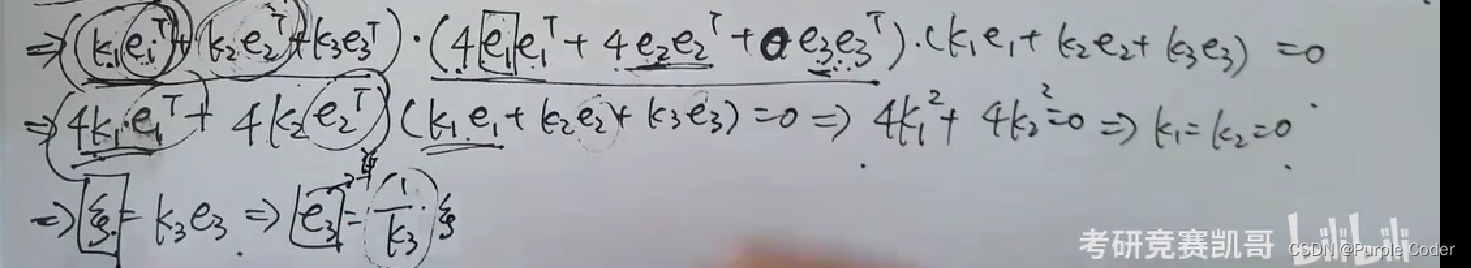
这篇关于二次型(感谢凯哥)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!
本文主要是介绍二次型(感谢凯哥),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!






求互相正交的向量

求参数C

对称矩阵和不对称矩阵永远不能合同
合同对角化

模板
目的


配方+线性方程组
一般变换:合同
正交变换: 相似







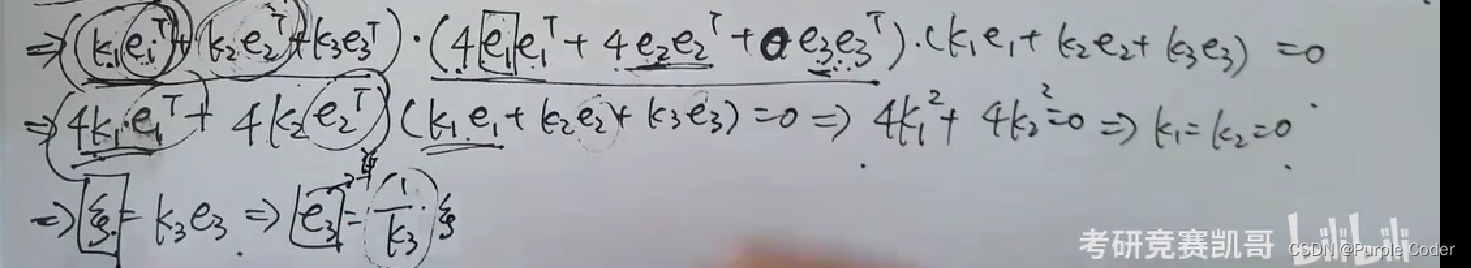
这篇关于二次型(感谢凯哥)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!
http://www.chinasem.cn/article/461145。
23002807@qq.com