本文主要是介绍考研数学线上笔记(八):凯哥方程组、特征值与特征向量、相似矩阵、二次型系列课程,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
- 特征值与特征向量
- 逆用矩阵乘法和相似求特征值
- 秩为1的矩阵,特征值为n-1个0和一个tr(A)(主对角线之和)
- 每行元素之和相同,特征值为该和;特征值也满足f(A)=0
- 迹是对角线之和,也是特征值之和;f(A)=0求出的是所有特征值的取值,但不是所有特征值
- 特征值相乘为行列式的值
- 伴随的迹是对角线位置的代数余子式之和
- 特征值:A^*^=|A|/λ
- 特征值对应一个特征向量;但特征值和特征向量之间没有倍数关系;
- 特征多项式一定是化零多项式
- 相似矩阵与相似对角化
- P^-1^AP=B,代表A与B相似
- 与对角阵相似的矩阵一定能够相似对角化,且特征值相同
- 两个矩阵相似,迹、行列式的值、特征值都必须相等;还是无法判断时,用r(A-λE)(必要条件)来做排除法
- 相似对角化的矩阵特征值相同
- 当A为秩一矩阵是,A能相似对角化与A的迹不为0等价
- 秩一矩阵可以分解成一列乘以一行,换个位置变成一行乘以一列算出的数就是该矩阵的迹
- 根据相似定义,利用对角阵计算
- 无解和无穷多解的区别:无解要求右边不为0,无穷多解要求右边为0
- 实对称矩阵
- 实对称矩阵的转置等于本身;实反对称矩阵的矩阵是其本身的相反数;实对称矩阵一定可以用正交矩阵进行相似对角化,即Q^-1^AQ=E
- 特征值完全相同 <--> 两个实对称矩阵相似;==内含实对称矩阵计算特征值的方法==
- 实对称矩阵一定相似对角化 --> 非零特征值个数恰好是r(A)
- (B^T^)^-1^= (B^-1^)^T^
- 特征值和特征向量大题
- 列向量组线性相关,必有|A|=0,一个特征值为0;逆用矩阵乘法后系数往往就是解
- 正交矩阵公式的运用
- 利用相似转化研究对象,注意别忘了AQ=QB转化的那一步;Q^-1^AQ=B代入M^-1^BM=∧,才能得出所求可逆矩阵P为QM
- 利用相似转化研究对象,能将未知的矩阵转化为已知矩阵求特征值
- 相似迹相同、行列式相同、特征是相同;求可逆矩阵使相似,一般求出各自的可逆矩阵P~1~、P~2~,联立即可
- 实对称矩阵一定相似对角化,所以非零特征值的个数等于秩,非满秩则必有特征值0,特征向量之间必正交
- 细节:同一特征值有两线性无关的特征向量才能推出是二重特征值;各行元素之和均为3,特征值有3;有特征值和对应的特征向量,反求实对称矩阵A时可以直接用上题解法
- A^n^=P∧^n^P^-1^,通过相似对角化转化为对角矩阵的n次方;非实对称矩阵不能用上面的方法,必须求逆
- 利用待定系数法求特征值和特征向量;正交矩阵Q的Q^T^就是Q^-1^,即Q^T^AQ=∧,就是Q^-1^AQ=∧;实对称矩阵取自不同特征值(数值不同)的特征向量必然正交,属于同一个特征值的无关的特征向量不一定正交
- 属于同一个特征值的特征向量相加,仍是特征向量;属于不同特征值的特征向量相加,不是特征向量
- 单特征值对应的特征向量是个直线,双特征值对应的特征向量是整个平面;三个互不相同的特征值,只知道一个向量时,不能直接用正交求其他两个特征向量(右下角的情况)
- 二次型的标准化与正定二次型
- 正(负)惯性指数即特征值为正(负)的个数;通过|A-λE|=0求出特征值的取值
- 具体矩阵的正定矩阵判别:顺序主子式(最左上角的1到n阶)都大于0,可以推出是正定矩阵;正定矩阵必是实对称矩阵,特征值全为正
- 标准型的系数就是特征值;特征向量乘个k,不会改变特征值
- 为防止出已配好的二次型不能可逆变换,应采取拆开的方法避免出错
- 等价、相似、合同的区别
- 相似必等价,合同也必等价,但反之不对;相似与合同没有必然关系,合同:正负惯性指数相同+同对称或同不对称,相似:特征值与特征向量对应相同
- 当AB都是实对称矩阵时,AB相似能推出AB合同;但合同矩阵不要求一定实对称,但要求同对称性
- 正负惯性指数对应相等,俩矩阵合同;从行列式的正负可以看特征值的正负
- 无特殊技巧时,计算特征值,特征值完全相等即相似(迹不一样就不相似),正负惯性指数对应相等时合同
- 实对称矩阵条件下,相似必合同,正负惯性指数相同
- 一个二次型转化为另一个二次型,二者合同
- 二次型大题
- 正交变换因Q^T^=Q^-1^,隐含AB相似,故迹相同,行列式相同
- 可逆变换求参数时,无上题的性质,只能通过正负惯性指数
视频链接:https://www.cctalk.com/m/program/1629431535446012
特征值与特征向量
逆用矩阵乘法和相似求特征值

秩为1的矩阵,特征值为n-1个0和一个tr(A)(主对角线之和)

每行元素之和相同,特征值为该和;特征值也满足f(A)=0

迹是对角线之和,也是特征值之和;f(A)=0求出的是所有特征值的取值,但不是所有特征值

特征值相乘为行列式的值
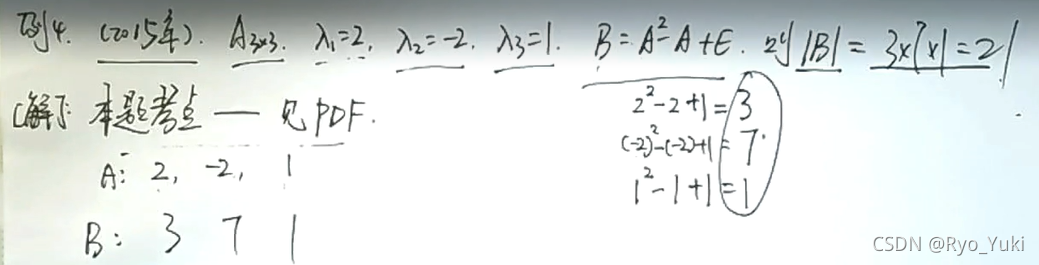
伴随的迹是对角线位置的代数余子式之和

特征值:A*=|A|/λ

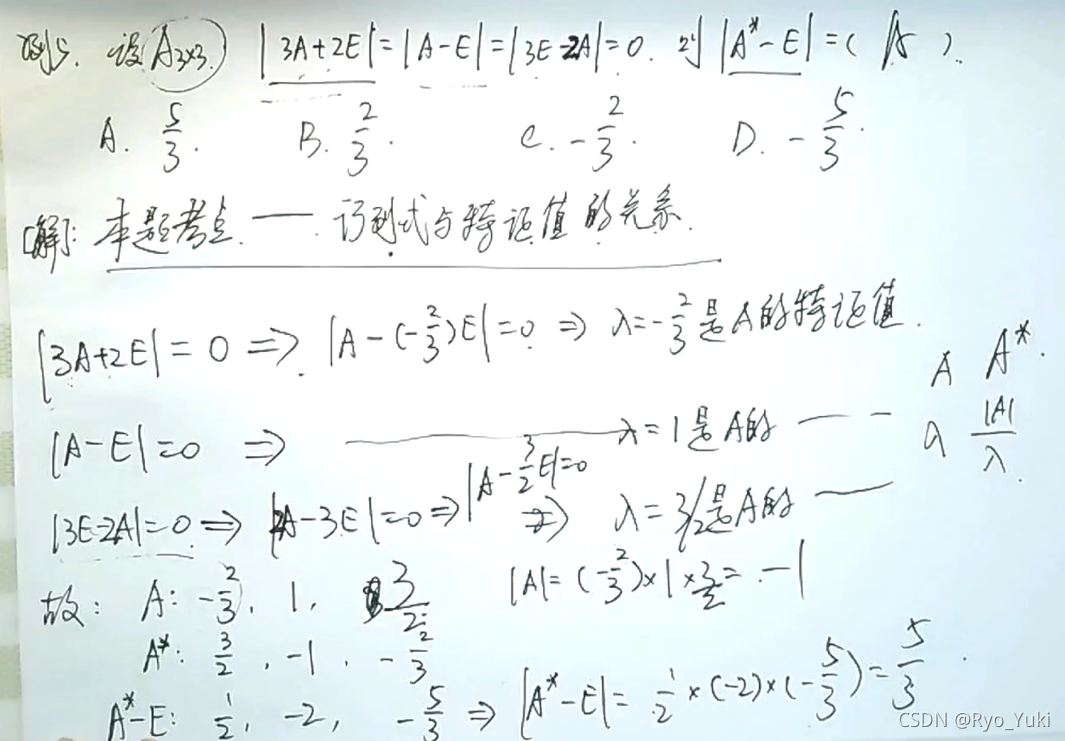
特征值对应一个特征向量;但特征值和特征向量之间没有倍数关系;

特征多项式一定是化零多项式

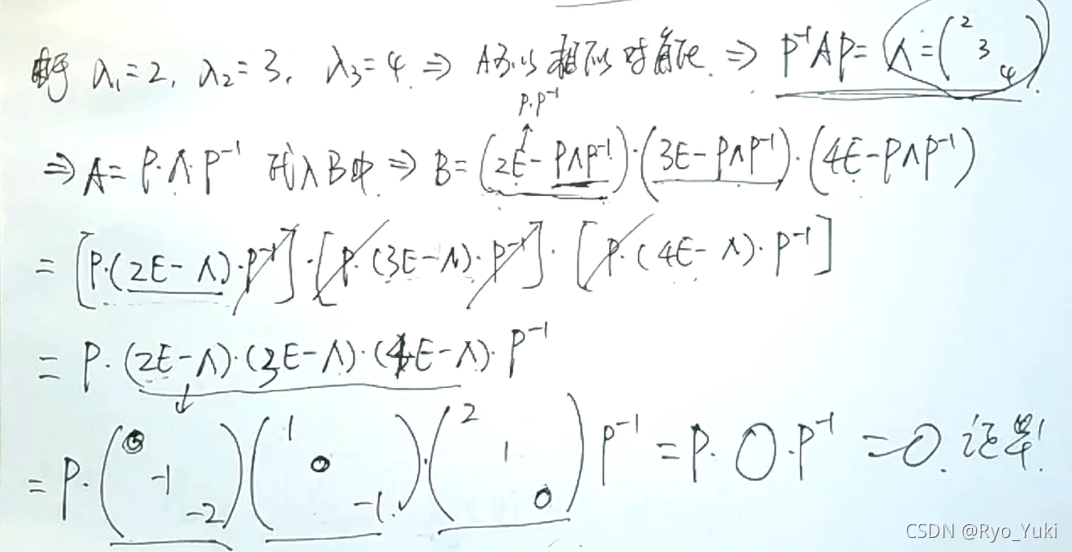
相似矩阵与相似对角化
P-1AP=B,代表A与B相似

与对角阵相似的矩阵一定能够相似对角化,且特征值相同

两个矩阵相似,迹、行列式的值、特征值都必须相等;还是无法判断时,用r(A-λE)(必要条件)来做排除法

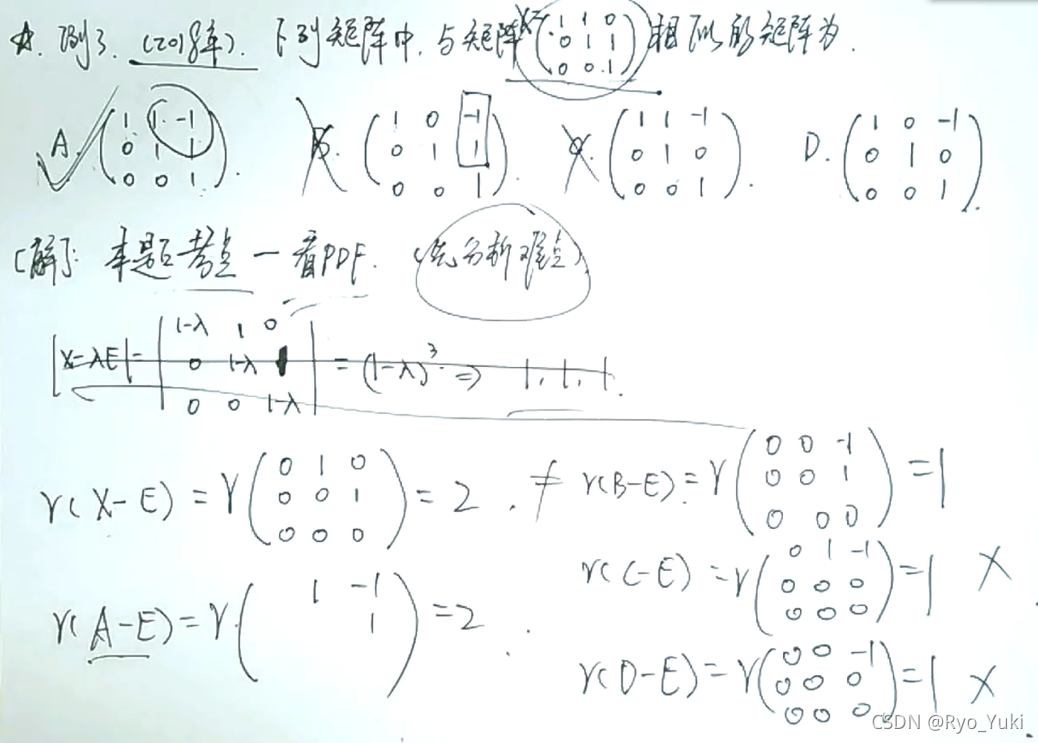
相似对角化的矩阵特征值相同

当A为秩一矩阵是,A能相似对角化与A的迹不为0等价

秩一矩阵可以分解成一列乘以一行,换个位置变成一行乘以一列算出的数就是该矩阵的迹

根据相似定义,利用对角阵计算
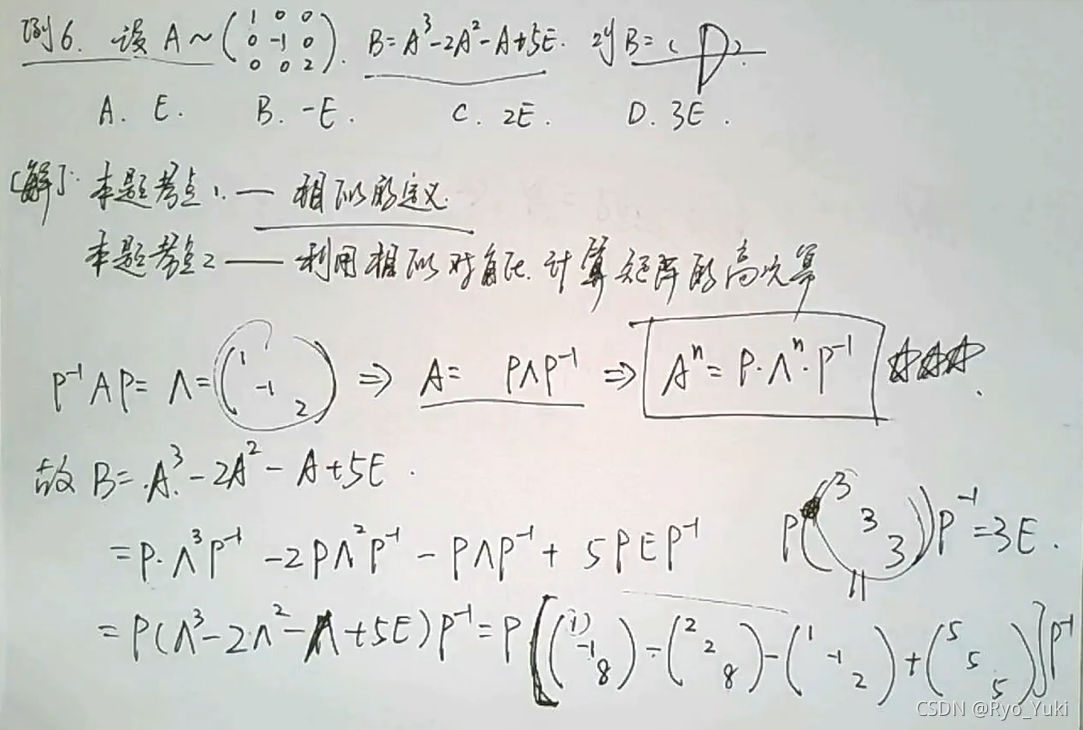
当然,用1、-1、2三个特征值分别用f(A)进行计算,也能算出对应的矩阵的特征值就是3、3、3
无解和无穷多解的区别:无解要求右边不为0,无穷多解要求右边为0

实对称矩阵
实对称矩阵的转置等于本身;实反对称矩阵的矩阵是其本身的相反数;实对称矩阵一定可以用正交矩阵进行相似对角化,即Q-1AQ=E

特征值完全相同 <–> 两个实对称矩阵相似;内含实对称矩阵计算特征值的方法
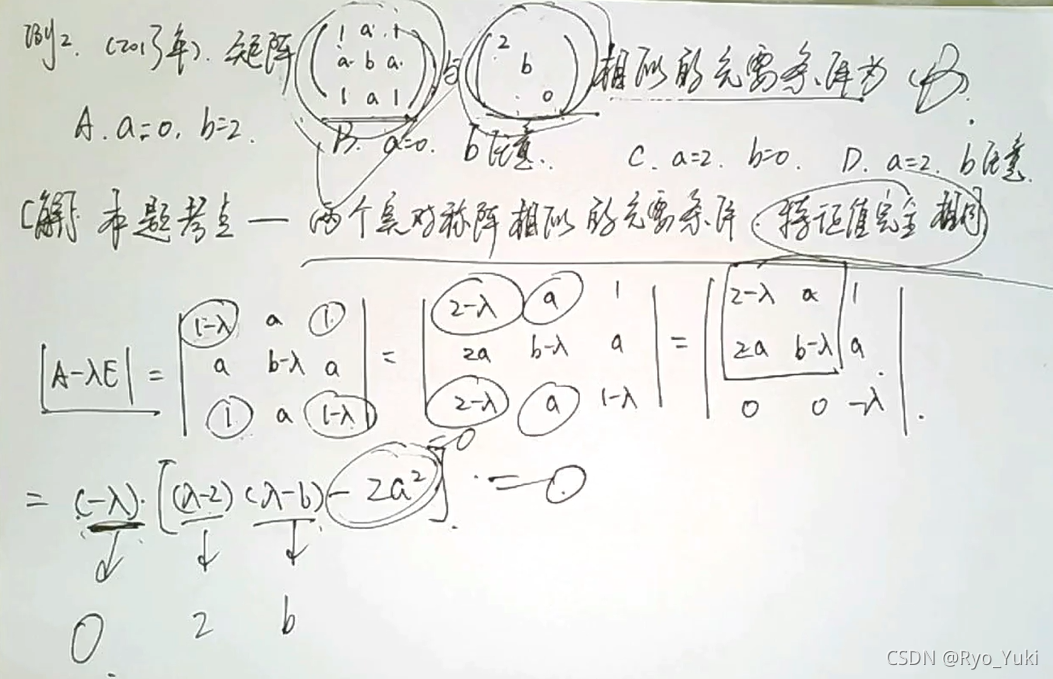
实对称矩阵一定相似对角化 --> 非零特征值个数恰好是r(A)

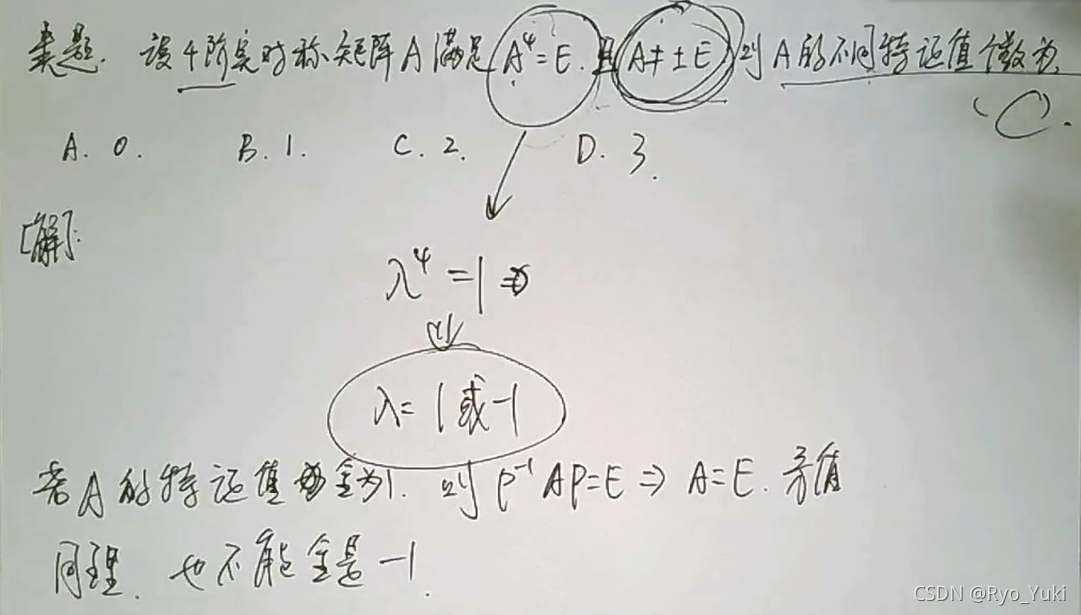
(BT)-1= (B-1)T

特征值和特征向量大题
列向量组线性相关,必有|A|=0,一个特征值为0;逆用矩阵乘法后系数往往就是解


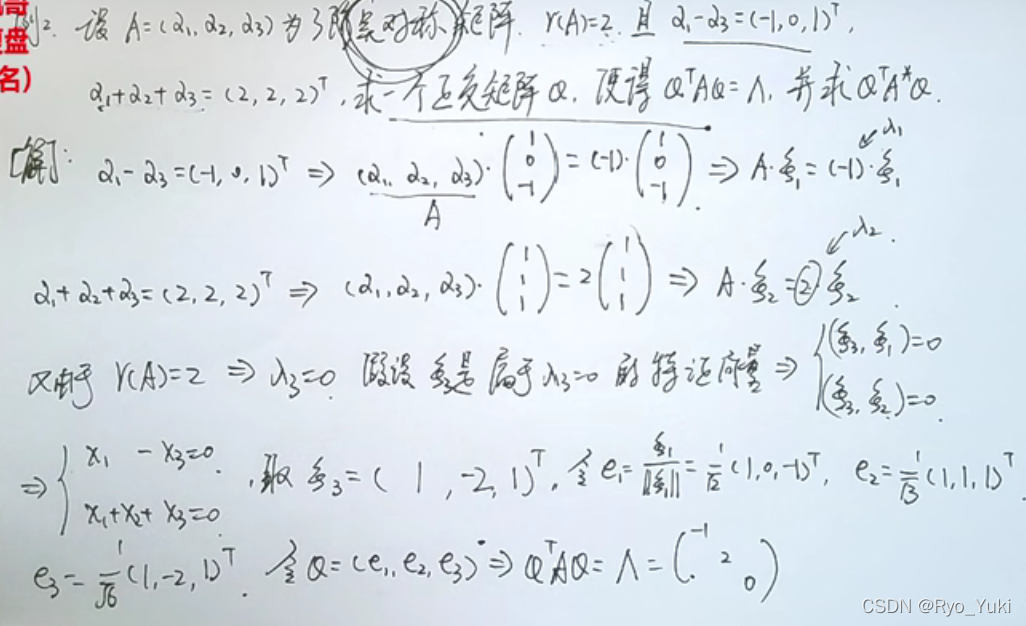
正交矩阵公式的运用
题目接上题

利用相似转化研究对象,注意别忘了AQ=QB转化的那一步;Q-1AQ=B代入M-1BM=∧,才能得出所求可逆矩阵P为QM

利用相似转化研究对象,能将未知的矩阵转化为已知矩阵求特征值


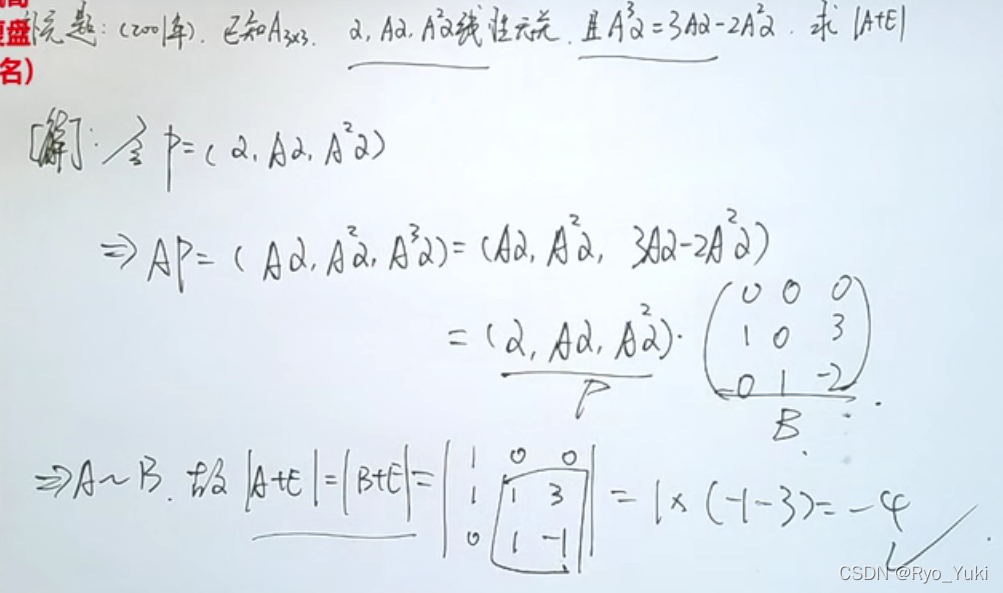
相似迹相同、行列式相同、特征是相同;求可逆矩阵使相似,一般求出各自的可逆矩阵P1、P2,联立即可

实对称矩阵一定相似对角化,所以非零特征值的个数等于秩,非满秩则必有特征值0,特征向量之间必正交

实对称矩阵因为向量间正交,有特征值和对应的特征向量,反求实对称矩阵A时可以直接用下面的方法,算出结果,试卷上假装还是用老办法算

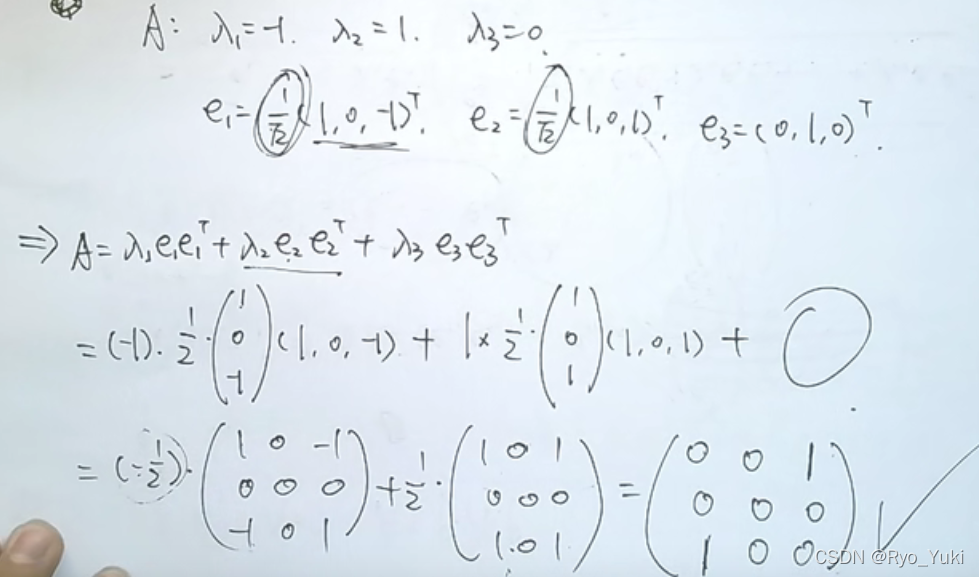
细节:同一特征值有两线性无关的特征向量才能推出是二重特征值;各行元素之和均为3,特征值有3;有特征值和对应的特征向量,反求实对称矩阵A时可以直接用上题解法

An=P∧nP-1,通过相似对角化转化为对角矩阵的n次方;非实对称矩阵不能用上面的方法,必须求逆
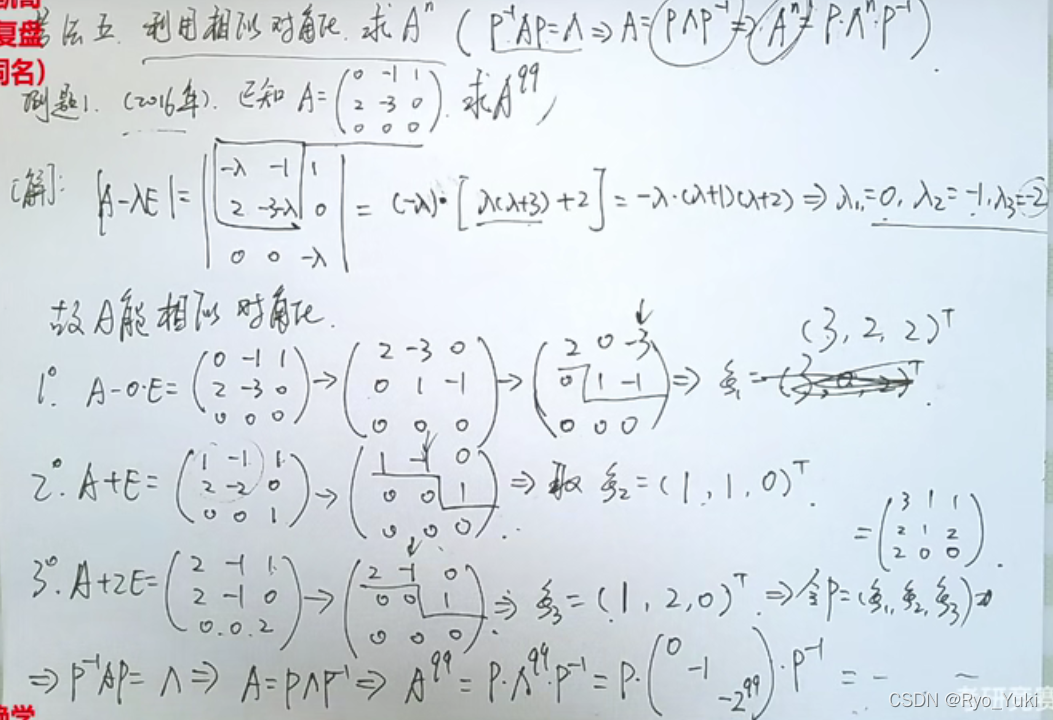
远古时代的真题的另一种An考法,

利用待定系数法求特征值和特征向量;正交矩阵Q的QT就是Q-1,即QTAQ=∧,就是Q-1AQ=∧;实对称矩阵取自不同特征值(数值不同)的特征向量必然正交,属于同一个特征值的无关的特征向量不一定正交

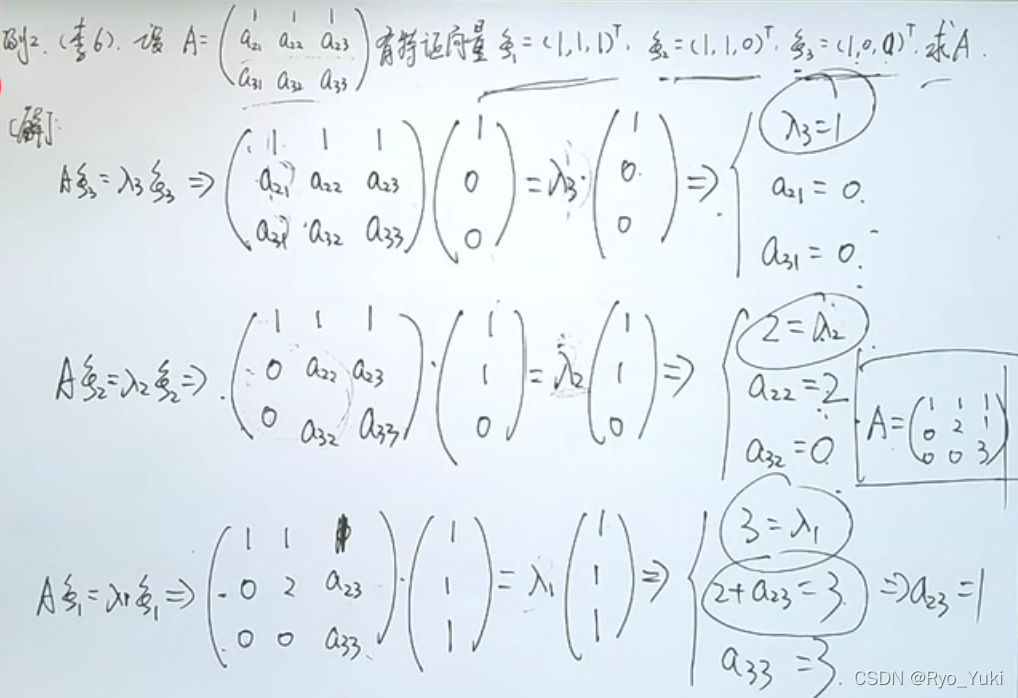
属于同一个特征值的特征向量相加,仍是特征向量;属于不同特征值的特征向量相加,不是特征向量

单特征值对应的特征向量是个直线,双特征值对应的特征向量是整个平面;三个互不相同的特征值,只知道一个向量时,不能直接用正交求其他两个特征向量(右下角的情况)
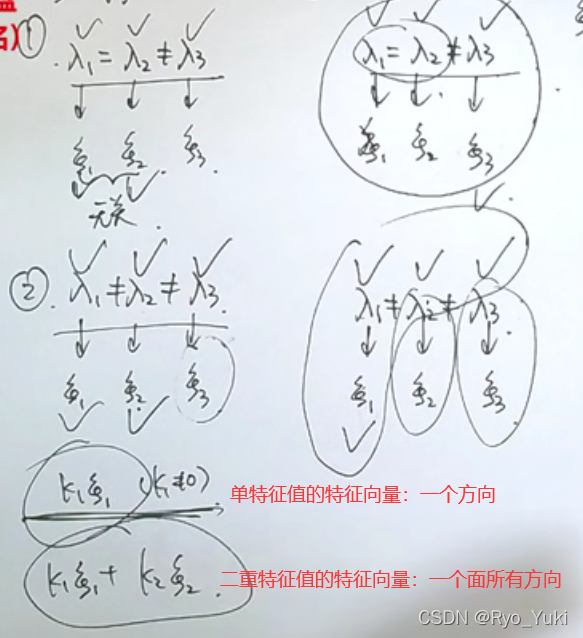
二次型的标准化与正定二次型
正(负)惯性指数即特征值为正(负)的个数;通过|A-λE|=0求出特征值的取值
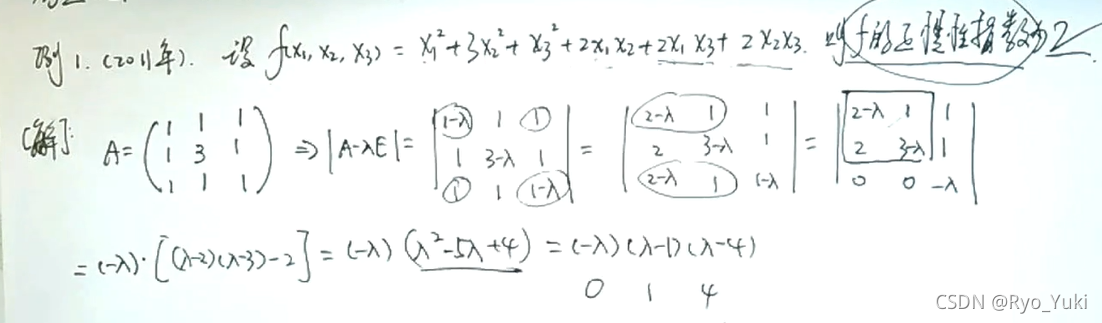
21年数三真题


具体矩阵的正定矩阵判别:顺序主子式(最左上角的1到n阶)都大于0,可以推出是正定矩阵;正定矩阵必是实对称矩阵,特征值全为正

标准型的系数就是特征值;特征向量乘个k,不会改变特征值



为防止出已配好的二次型不能可逆变换,应采取拆开的方法避免出错
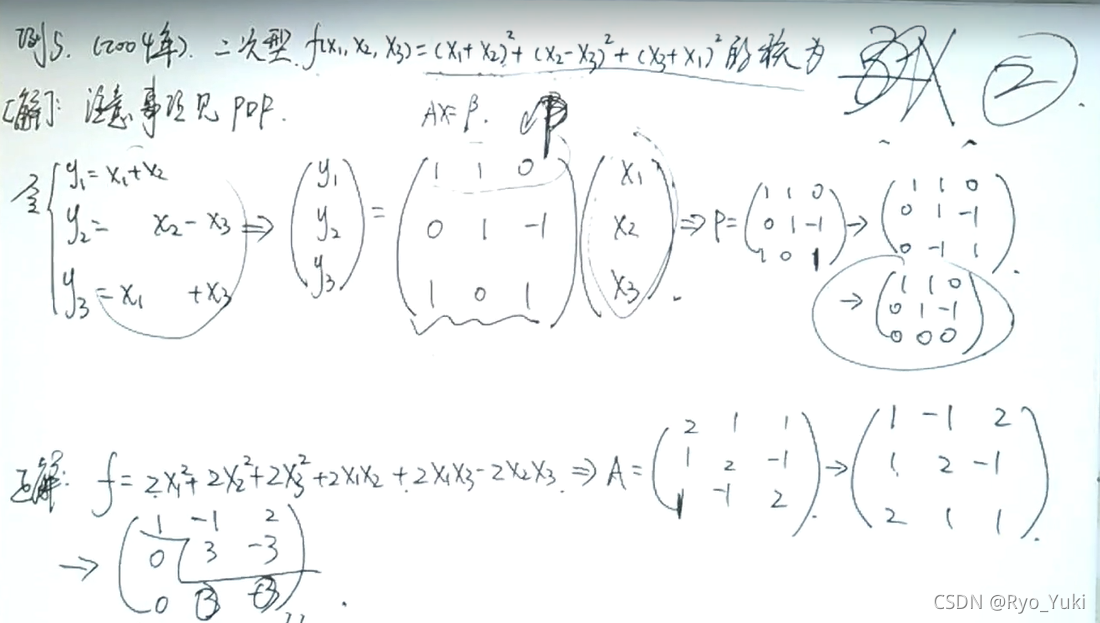
等价、相似、合同的区别
相似必等价,合同也必等价,但反之不对;相似与合同没有必然关系,合同:正负惯性指数相同+同对称或同不对称,相似:特征值与特征向量对应相同


当AB都是实对称矩阵时,AB相似能推出AB合同;但合同矩阵不要求一定实对称,但要求同对称性

正负惯性指数对应相等,俩矩阵合同;从行列式的正负可以看特征值的正负

无特殊技巧时,计算特征值,特征值完全相等即相似(迹不一样就不相似),正负惯性指数对应相等时合同


实对称矩阵条件下,相似必合同,正负惯性指数相同
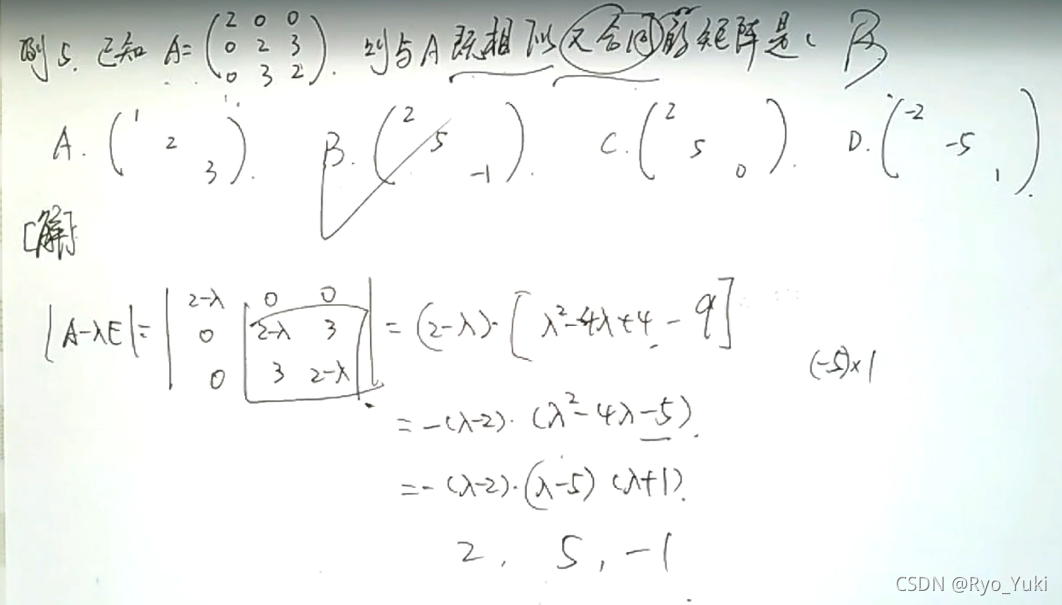
一个二次型转化为另一个二次型,二者合同

二次型大题
正交变换因QT=Q-1,隐含AB相似,故迹相同,行列式相同

可逆变换求参数时,无上题的性质,只能通过正负惯性指数
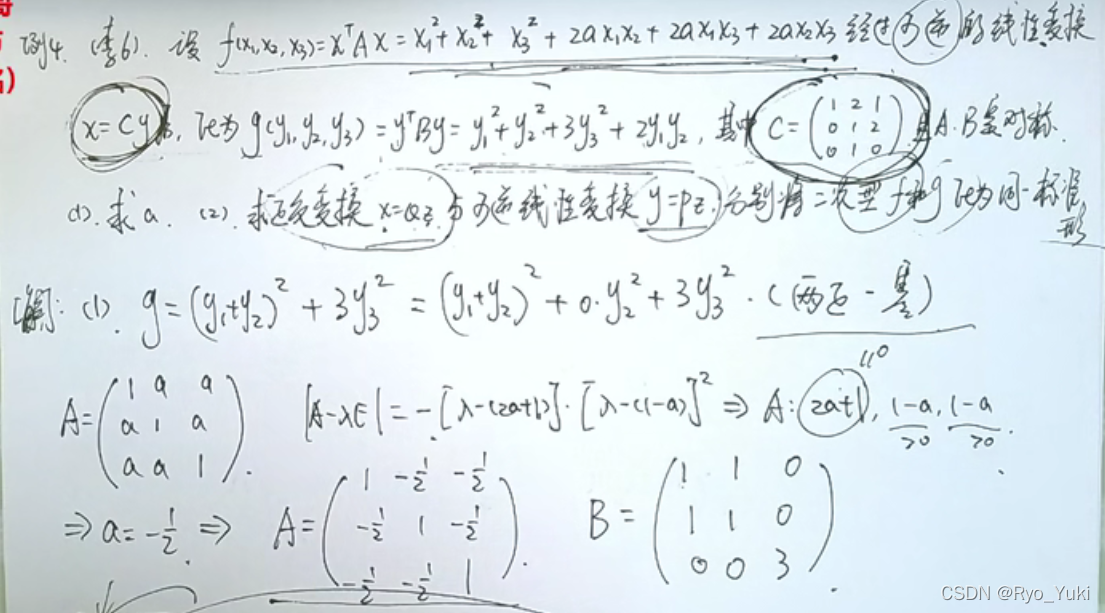
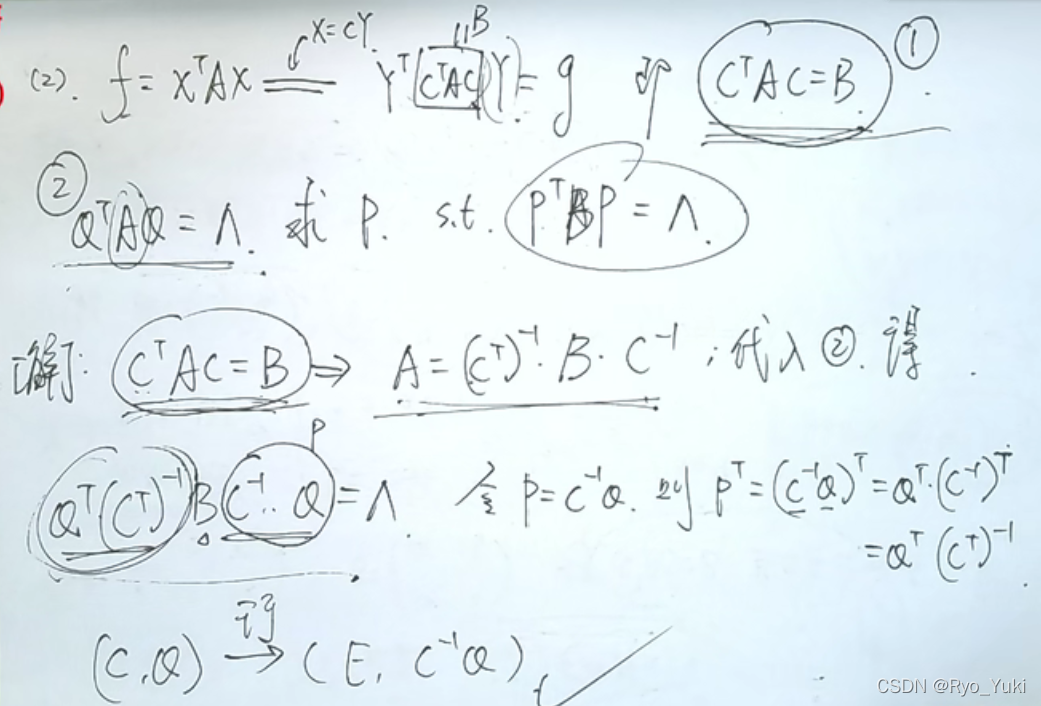
这篇关于考研数学线上笔记(八):凯哥方程组、特征值与特征向量、相似矩阵、二次型系列课程的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








