本文主要是介绍Geodesic in Heat: 一种测地线计算方法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
在之前的博客中，我已经介绍过了使用Fast Marching算法计算测地线。Fast Marching的好处是实现简单，方便扩展在点云上。但是缺点是精度不够，求解不平滑。早在2013年，Crane et al. [1]就已经提出利用热流来估算测地距离。我很早就知道这个解决方案，大概是利用了拉普拉斯余切权重来实现一个二阶偏微分计算，以获得更精确的结果。这次恰好要做点云上的测地线计算，就把原文下载下来好好的学习一下。不看不知道，一看吓一跳，方法设计的很精巧，数学符号很花哨，对我浅薄的微分几何基础认知带来了极大的挑战。我决定在这篇博客中浅谈一下对这篇文章的理解，起到一个抛砖引玉的作用，如果有写错的地方，诚恳的希望高手指点，也让我提升一下。
1. 基本思路
Geodesics in heat的基本思路相对容易理解。首先估算一个基于热流的标量函数，之后对该标量函数对应的梯度向量场进行归一化计算，再用Possion方程平滑一下，即得到最后对测地距离场的精确估算。在Fast Marching算法中，我们已经知道了利用波动方程求解测地距离的一个离散方法。缺点是对钝角三角形敏感。究其原因，是因为点的位置关系不是规则的，或非各向同性的。这使得由一个源点向四周扩散时，计算外边的点到源点的距离时，不能直接相关的边累加，而是要通过一个微分方程间接的求解一种平滑的能力传递，以获得准确的结果。一点在接收他相关的点传递给他的能量或者累计距离时，需要考虑更复杂的标量函数平滑条件，而非直接连接一条边。如果你读不懂上述文字，没关系，看一个例子你就明白了：
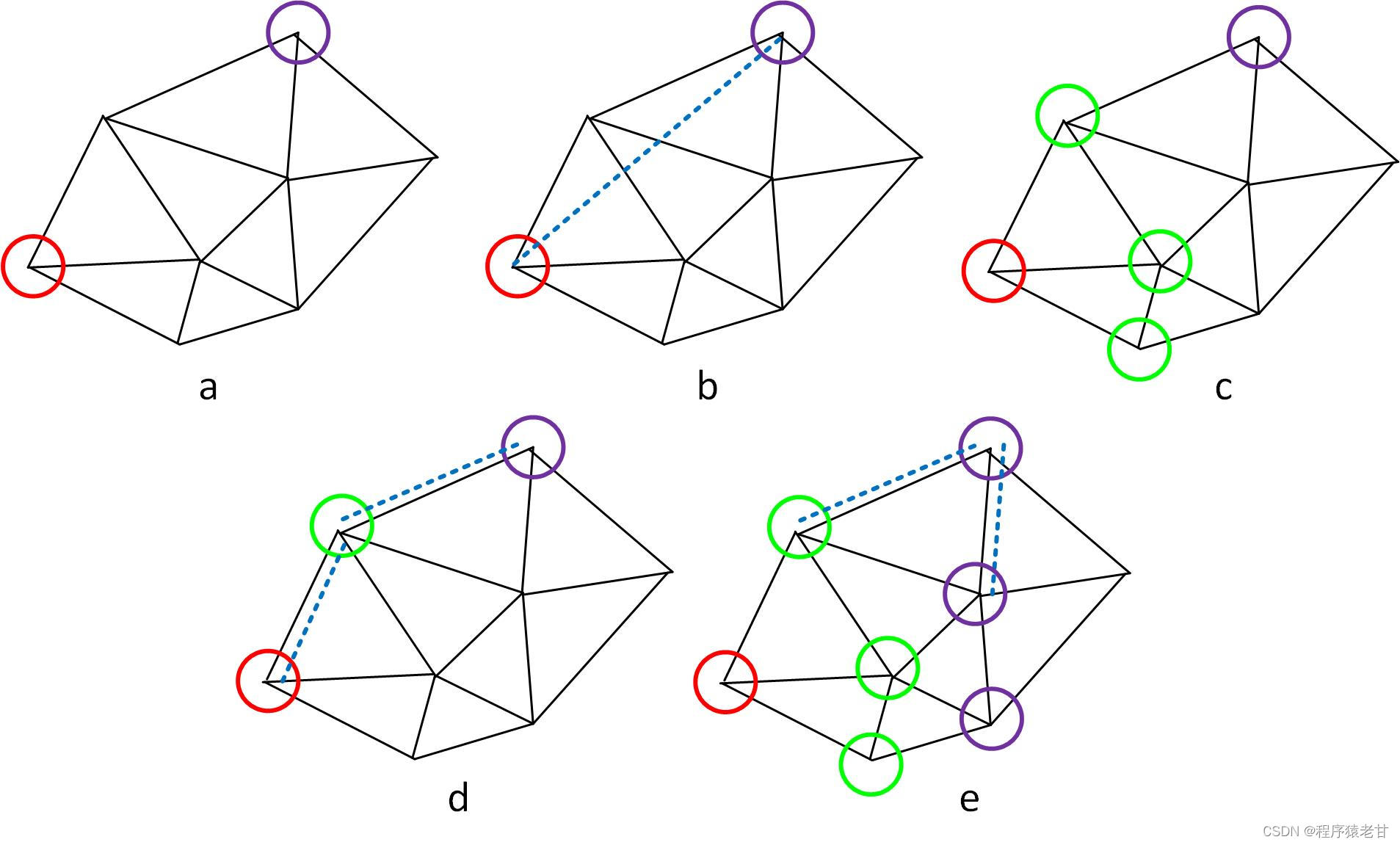
这里假设由一个离散网格（2-manifold），我们希望计算红色点到紫色点的距离（a）。最直接的想法是直接计算他们的欧氏距离（b）。显然，这不是测地距离，因为已经脱离了网格本身。那么，我们需要逐步的计算测地线，即首先找到红色点的一邻域点，即绿色点（c）。在绿色点的基础上，我们在迭代搜索其一邻域，直到找到紫色点，累加边的长度就得到一个测地线的近似（d）。这个计算比欧氏距离好一些，但是显然还是不够精确。因为我们没有考虑距离传递是要以源点为起点的，叠加边界相当于不断改变源点，即改变了距离传递的方向。我们希望距离的传递在某一个方向上是平滑的。假设有这样一个函数，在每一个点上有一个标量值。我们希望这个函数的标量值对应测地距离，那么这个函数的梯度应该是恒定的。求测地线距离即转换成了求标量函数。回顾一下之前的步骤，我们利用局部的网格来构建一种点的关系（e），这种关系用来显性的表示函数的梯度。利用梯度，我们就能够通过微分方程，反向求解出函数，获得每个点的标量值。这就是利用微分方程求解测地线距离的核心思想。
Geodesics in heat的核心思想符合上述的描述，该方法利用物理上的热流，首先估计一个标量函数。这个标量函数的值对应一种粗糙的测地距离估计。其最大的问题就是梯度不均衡。作者在此基础上，通过对该标量函数的梯度归一化，而后解一个Possion方程，得到对原始标量函数的平滑。平滑后的标量函数即对应最终的测地距离估计。这个方案的好处是，通过两个简介的分段线性方程求解，以求解非线性的测地线计算问题。上述计算并未严格要求数据格式，可以方便扩展在任意的三维数据上，如体素、点云、多面体等。
2. 算法步骤
Geodesics in heat的总共包括三个步骤，即对热流标量函数求解，梯度归一化，最后解Possion方程。作者在论文中给出了对应的步骤：
论文在开始处就提高了基于热核的测地线显性表示：
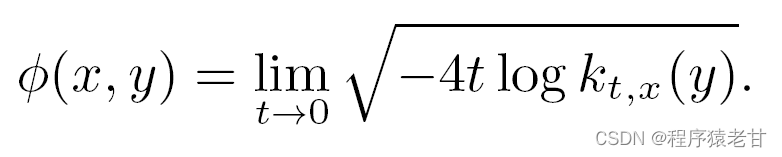
Φ表示测地距离，x，y表示两个顶点，t表示事件，k表示heat kernel。我的理解是，当t足够小的时候，热量传导的距离即对应测测地距离。这里作者提议用大量的篇幅指出，热核推出的标量函数智能被认为是测地距离的粗糙拟合。只有在梯度均衡的情况下，其拟合结果的精度才能被保证。其误差被表示为下图：
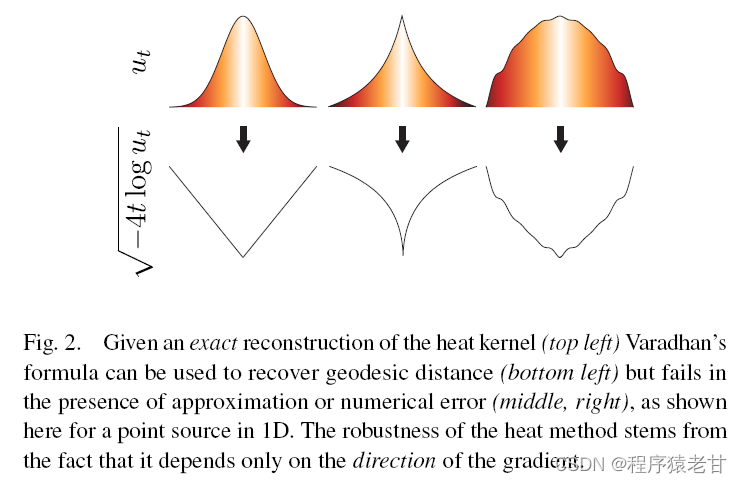
因此，当利用热核求解处标量函数后，需要对梯度进行归一化，再解一次Possion方程才能获得精确的测地线拟合结果。（上面那个图我并没有看懂，猜测是说测地线在流形上的距离传播应该是线性的，但是热核函数的拟合误差，在实际计算时，会产生非线性的结果）。作者另外给了一个图，来进一步说明这种非线性变化的差异：
左图为热核推出的标量函数结果，右图为Possion方程求解后的结果。
这样，我们就大致了解了Geodesics in heat的三个求解步骤：
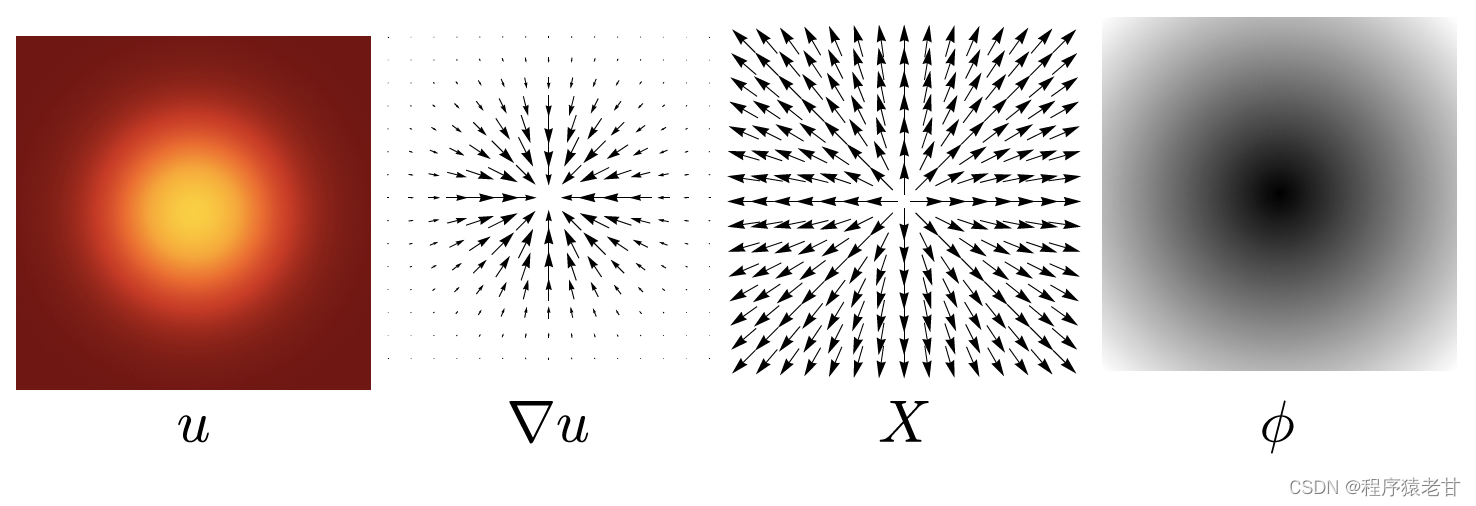
即首先获得热核推导的标量函数u，对应一个非均匀的梯度分布▽u，对▽u归一化，得到向量场X，基于X，解Possion方程，获得最后的标量函数Φ，即对应测地距离。
在面片上的计算方法
如果你对上述描述完全不感冒，不用担心，直接给网格计算的实例，或许能够启发你对整个求解过程的理解。首先我们给出一个点的拉普拉斯离散表示：
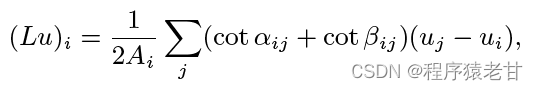
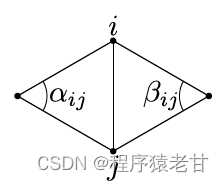
这里的网格和前面的网格实例是一样的。我们希望求从一个源点出发，到i和j两点的测地距离ui和uj。ui和uj基于他们相关边夹角的关系即构成了一个点的拉普拉斯表示，你可以简单理解为点与点的权重关系。Ai为面积元素，值为与i点相关的所有面片的面积的1/3。我们把所有点的拉普拉斯离散表示构建成一个矩阵形式：
A即Ai构成的n*n的diagonal matrix，Lc为n*n的余切权重算子，两项刚好对应前边Lu的计算过程。基于Lc和A我们就能够列出一个求Heat flow的方程：
t为时间，我查了作者的报告，这个t的取值对于估算结果是有影响的：
作者建议根据实际误差的考察，t取h^2,h为全局平局距离：
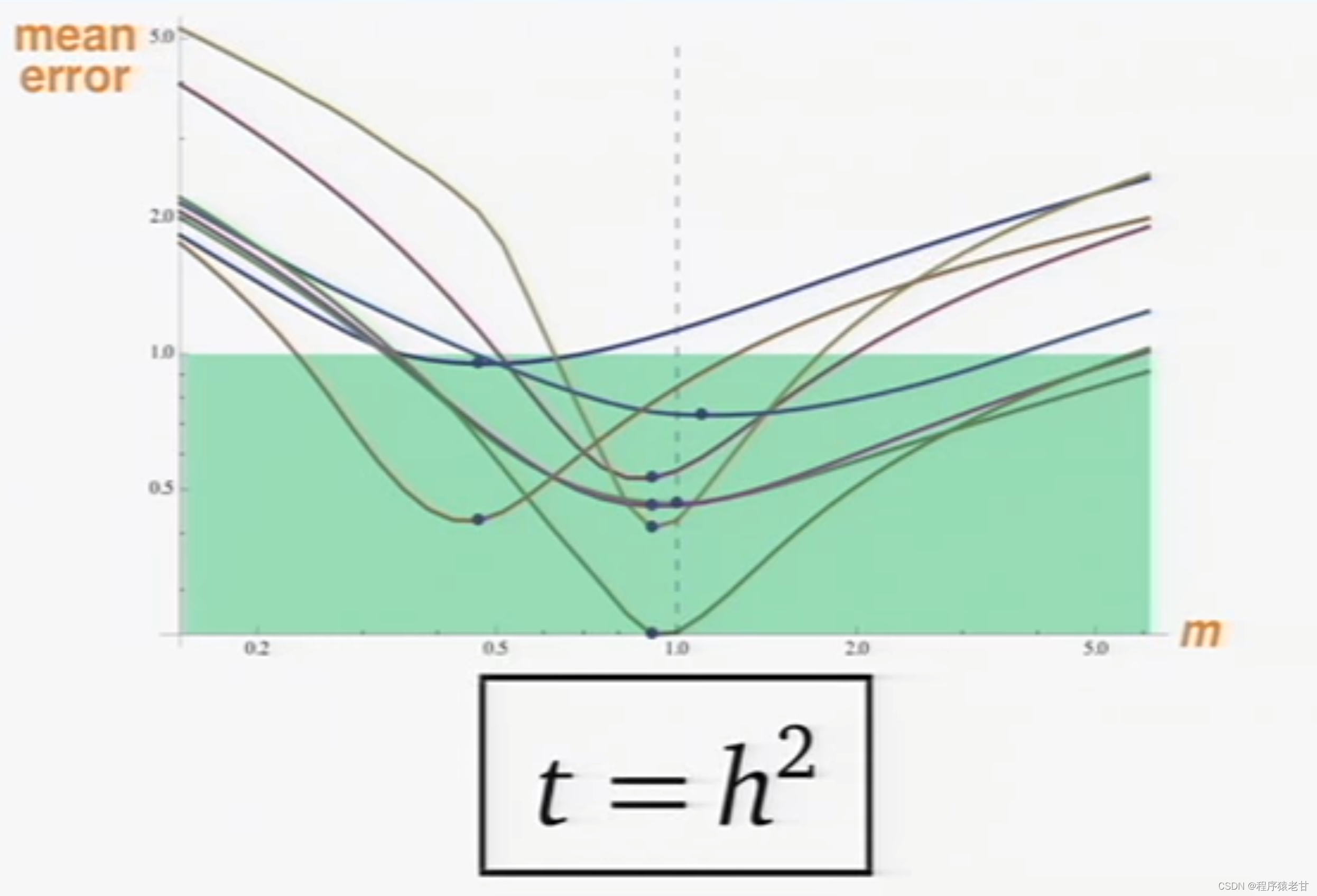
为Kronecker delta（克罗内克δ函数），即一个二值函数，源点为1，其余点为0。这样我们对对方程(A-tLc)u=δ的各项进行了规定，以求解u，即热流对应的标量函数。
之后我们对u求其梯度：
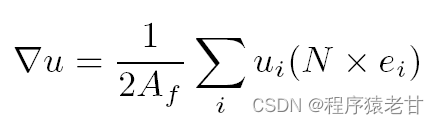
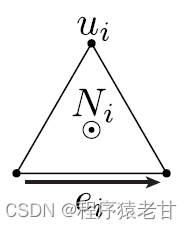
N为面片的单位法向，其他量对应图片可以很容易的理解。在对u的梯度进行归一化获得新的梯度场X，而后对X列出拉普拉斯，即
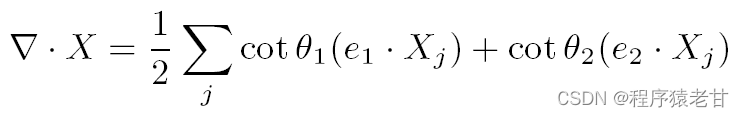
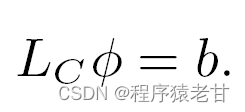
b即为
，上述方程即利用Possion方程对Φ求解。如果你熟悉拉普拉斯线性系统求解问题，那么到这里，你就可以利用线性求解方法，得到Φ，即基于某一源点的测地距离。有兴趣了解具体解法的同学，可以参考我的另外一篇博客：基于测地距离场的三维人脸参数化方法
看到这里，又想起当年微分几何老师那句经典的话，如果几何分析只有一个重要的概念，那个概念就是拉普拉斯，老师诚不欺我！Crane还介绍了在点云计算的方法，大体利用的是维诺图建立局部邻接关系，这里不再展开。
这里展示一些结果图，整体来说，还是非常精巧的一个解法：
Reference
[1] Crane K, Weischedel C, Wardetzky M. Geodesics in heat: A new approach to computing distance based on heat flow[J]. ACM Transactions on Graphics (TOG), 2013, 32(5): 1-11.
这篇关于Geodesic in Heat: 一种测地线计算方法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
