基于粒子群算法思想的电动汽车充放电策略-V2G模型-程序代码！

本文主要是介绍基于粒子群算法思想的电动汽车充放电策略-V2G模型-程序代码！，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

电动汽车充放电对电网的安全稳定带来影响，合理规划电动汽车充放电时间和策略是目前的研究热点。本程序仿真了汽车有序充电和无需充电两种案例，利用电动汽车合理消纳新能源电量，利用粒子群算法思想来求解模型，程序中案例丰富，注释清晰，干货满满，下面对程序进行简要介绍！

创新点：

1、在保证电动汽车用户出行需求的前提下，为了使工作区域电动汽车尽可能多的消纳供给商场基础负荷剩余的光伏电量，根据光伏出力与工作区负荷的偏差制定动态分时电价模型，从而减少峰谷差，保障电网稳定性，同时能够提高电动汽车用户的充放电满意度，实现双赢。

2、配电网负荷方差最小目标函数包含了工作区常规负荷、光伏出力及电动汽车的充放电电量，应用了电动汽车源-荷二重性。

3、本程序较为基础，可扩展性强，稍加利用就可创新！

程序结果：

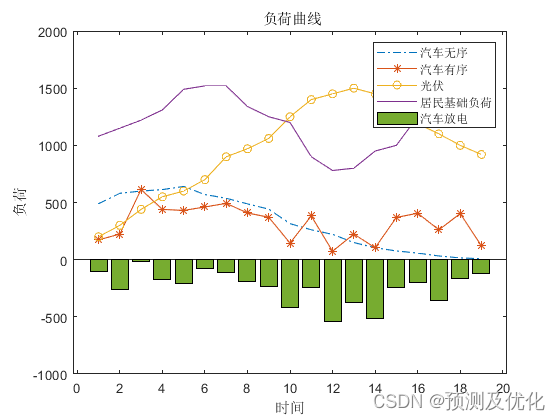
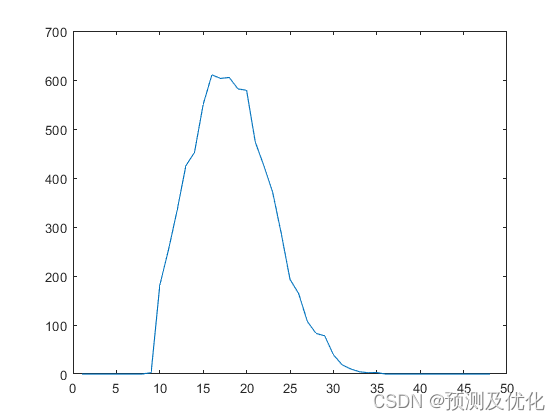
部分程序：

%% 算法参数
parameter;
close all;
global PV_load Power_load number_ car_data soc_end  EV_loadMaxIt=300;      % Maximum Number of Iterations
nPop=250;        % Population Size (Swarm Size)[all_load]=xlsread('data','Sheet1','b2:d20');%负荷PV_load=all_load(:,1)*1;%光伏负荷Power_load=all_load(:,2)*1;%用电负荷[car_data]=xlsread('data','Sheet1','e2:h51');%无序负荷
%  [load_car,car_start,car_leave,car_soc ]= c_car_load(car_number);%电动汽车无序负荷
load_car=car_data(1:48,4);EV_load=load_car(14:32);%电动汽车无序负荷car_start =car_data(:,1);car_leave=car_data(:,2);car_soc=car_data(:,3)-0.1;soc_end=soc_endzi();
car_in=car_start;car_off=car_leave;%% 确定变量for i=1:car_numbercar_in(i)=fix(car_start(i)/30);car_off(i)=fix(car_leave(i)/30);      enddiaodu_carin=[];%可调度diaodu_caroff=[];%可调度diaodu_soc=[];%可调度diaodu_socend=[];jishu=0;%可调度diaodu_carin_=[];%bu可调度diaodu_caroff_=[];%bu可调度diaodu_soc_=[];%bu可调度diaodu_socend_=[];jishu_=0;%bu可调度for i=1:car_numberif car_in(i)>=14&&car_off(i)<=32jishu=jishu+1;diaodu_carin(jishu)=car_in(i);diaodu_caroff(jishu)=car_off(i);diaodu_soc(jishu)=car_soc(i);diaodu_socend(jishu)=soc_end(i);elsejishu_=jishu_+1;diaodu_carin_(jishu_)=car_in(i);diaodu_caroff_(jishu_)=car_off(i);diaodu_soc_(jishu_)=car_soc(i);diaodu_socend_(jishu_)=soc_end(i);endend
[m ,n]=size(diaodu_carin);%n为19，19辆车可调度
number_=zeros(n,1);
for i=1:nnumber_(i)=diaodu_caroff(i)-diaodu_carin(i)+1;
end
number_;
sum(number_);%变量个数最终确定nVar=sum(number_);              % Number of Decision VariablesVarMin=P_discar*30;VarMax=P_chscar*30;

以上就是本次介绍的主要内容，欢迎感兴趣的小伙伴关注下方公众号获取完整版代码，小编会继续推送更有质量的学习资料、文章和程序代码！