TZOJ 1373 求多项式的和

本文主要是介绍TZOJ 1373 求多项式的和，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

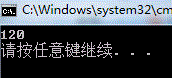
答案：

#include <stdio.h>  
int main() 
{int m = 0;scanf("%d", &m);  // 读取测试实例的个数  while (m--)   //循环m次{int n = 0, i = 0;scanf("%d", &n);  // 读取求和项数n double sum = 0.0;for (i = 1; i <= n; i++)   //分母从1开始一直到n（即为前n项）{if (i % 2 == 0)   //若为偶数项就为减{sum -= 1.0 / i;   //1.0使得除出来的值是小数}else    //若为奇数项就为加{sum += 1.0 / i;   //1.0使得除出来的值是小数}}printf("%.2f\n", sum);  // 输出前n项的和，保留2位小数  }return 0;
}

知识点：

两个int类型相除不会得到小数，例如3/2只能得到1，如果想得到具体小数，只需让除数或被除数有一个是浮点型就行（不需要两个都是浮点型），例如3.0/2或者3/2.0都可以得到1.5

这篇关于TZOJ 1373 求多项式的和的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---