清华AI自强计划作业2实验

本文主要是介绍清华AI自强计划作业2实验—逻辑回归模型，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

问题：

运行模型输出loss值为NAN,训练200次后未出现线性模型
在这里插入图片描述

nan

nan的数据类型为float, not a number 的缩写。python中判断是否为nan类型的方法，使用math库中的*isnan()*函数判断：

from math import isnan
import numpy as np
res = np.nan
print (isnan(res))

无法确定运算结果时会返回nan结果.

回到问题本身：
bug出现在交叉熵损失函数的计算中:

sum_err -= Y[i]*np.log(Y_[i])+(1-Y[i])*np.log(1-Y_[i]

其中Y[i]为真值，Y_[i]为对应数据的预测值。
将np.log(Y_[i])打印出来发现类型为 -inf：负无穷大
发现在数据归一化过程中，

Xmin = X.min(0)# 每列的最小值，输出行为1列为2的数组 # 通过使用 np.min 函数，计算原始数据沿着 axis=0 方向的最小值，即：求每一列的最小值，并赋值给 Xmin
Xmax = X.max(0)# 通过使用 np.max 函数，计算原始数据沿着 axis=0 方向的最大值，即：求每一列的最大值，并赋值给 Xmax
Xmu = np.mean(X)#

注意np.mean函数的用法：
np.mean(X,axis, out，keepdims)
axis为0，表示压缩行，按列取均值，返回1n矩阵
axis为1，表示压缩列，按行取均值，返回m1矩阵
那么在上述代码中，Xmu应当为np.mean(X,0)，对各列取均值，下面的归一化公式才可以计算正确：

X_norm = (X-Xmu)/(Xmax-Xmin)

修改Xmu = np.mean(X,0)后
显示x_norm的值为：

在这里插入图片描述
原始数据绘图：
可以看到横轴纵轴的刻度全部依照真实数据

归一化输出结果是这样的：

横轴和纵轴均分别归一化处理
拟合线性模型为：在这里插入图片描述

输出损失值和准确值
Cost theta: [[ 0.48518509]]
Train Accuracy: 0.88

在批量梯度下降法中（Batch Gradient Descent，BGD）,不断更新权重 W

def BGD(X, y, iter_num, alpha):
trainMat = np.mat(X) # 通过使用 np.mat 函数，将数据集 X 转换成矩阵类型，并赋值给 trainMat,trainMat的类型为ndarray,m3(在月薪和身高两列之外，新增全为1的一列)
trainY = np.mat(y).T # 通过使用 np.mat 函数，将数据集 y 转换成矩阵类型，并且转置，然后赋值给 trainY
m, n = np.shape(X) # 通过使用 np.shape 函数，得到数据集 X 的形状大小，其中，m 为数据集 X 的行数，n 为数据集 X 的列数
w = np.ones((n, 1)) # 通过使用 np.ones 函数，创建元素全为 1 的矩阵，矩阵的大小为 n 行 1 列，并赋值给 w, 即：进行权重 w 的初始化，令其全为 1
for i in range(iter_num): # 通过 for 循环结构，开始进行迭代，其中，i 可取的数依次为：0，1 ，2，…，iter_num-1，迭代次数总共有 iter_num 次
error = sigmoid(trainMatw)-trainY # 计算迭代的误差 error：将预测得到的激活函数的数值 sigmoid(trainMatw) 减去实际的 trainY 数值
w = w-(1.0/m) * alphatrainMat.Terror # 更新权重 w , BGD 批量梯度下降法的核心， w = w - (1.0/m)alphatrainMat.Terror
return w # 返回 w’

sigmoid函数实现：

wx为m1矩阵，sigmoidV计算结果也为m1矩阵
def sigmoid(wx):
sigmoidV = 1.0/(1.0+np.exp(-wx))# 请补全
# 请补全计算激活函数 sigmoid 函数的函数值，计算公式为：1.0/(1.0+np.exp(-wx))
return sigmoidV

iter_num为迭代次数，设m为数据行数
trainMat：m*3（第一列为1，第二列为身高标签归一化数据，第三列为月薪标签归一化数据）
w：3*1（初始化为全1矩阵，分别对应月薪参数、身高参数和偏置）
sigmoid函数返回矩阵：m*1
trainY：m*1
error :m*1 每组数据在此模型下的误差
trainMat.T * error ：3*1 ，和w的矩阵格式相同，因此可直接加减。

批量梯度下降法

每次使用所有样本来进行函数的更新，
目标函数：
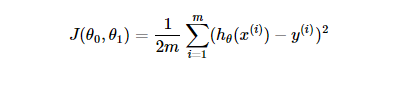
在这里插入图片描述
更新参数的方式：

在这里插入图片描述

代码中使用矩阵运算实现了公式中求和的功能，和代码结合食用效果更佳！

ps：
根据课程群里有同学提出的归一化的问题，也亲自做了实验：
在当前数据下，减去均值和中位数进行归一化是没什么区别的，cost值略有差别：

def normalization(X):
Xmin = X.min(0)# 每列的最小值，输出行为1列为2的数组 # 请补全通过使用 np.min 函数，计算原始数据沿着 axis=0 方向的最小值，即：求每一列的最小值，并赋值给 Xmin
Xmax = X.max(0)# 通过使用 np.max 函数，计算原始数据沿着 axis=0 方向的最大值，即：求每一列的最大值，并赋值给 Xmax
Xmu = np.median(X,0)#通过使用 np.median函数求该列数值的中位数，计算原始数据均值，并赋值给 Xmu
X_norm = (X-Xmu)/(Xmax-Xmin)# 计算归一化后的数据，归一化公式为：(X-Xmu)/(Xmax-Xmin)，归一化后数据范围为 [-1,1]
return X_norm # 返回数据预处理，归一化后的数据 X_norm

在这里插入图片描述