本文主要是介绍matlab 决策树分类调参,ID3决策树算法 - osc_dwi1do0o的个人空间 - OSCHINA - 中文开源技术交流社区...,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一,简介
ID3(Iterative Dichotmizer 3)
1.什么是决策树学习
决策树学习是以训练或样本数据集为基础的归纳学习算法,是用于分类和预测的重要技术。
2.ID3核心思想
核心思想是利用信息熵原理选择信息增益最大的属性作为分类属性,递归地拓展决策树的分枝,完成决策树的构造
3.决策树学习本质是什么
决策树学习本质上是从训练数据集中归纳出一组分类规则
二,基础概念
a.信息熵
熵(entropy)表示随机变量不确定性的度量,也就是熵越大,变量的不确定性就越大。设
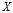 是一个有限值的离散随机变量,其概率分布为:
是一个有限值的离散随机变量,其概率分布为:
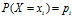 ,
,
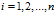
则随机变量
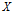 的熵定义为
的熵定义为
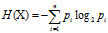
(若
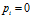 ,定义
,定义
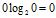 )
)
b.条件熵
条件熵
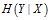 表示在已知随机变量
表示在已知随机变量
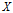 条件下随机变量
条件下随机变量
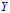 的不确定性。随机变量
的不确定性。随机变量
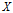 给定的条件下随机变量
给定的条件下随机变量
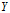 的条件熵为
的条件熵为
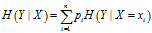 ,
,
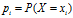
c.信息增益
特征
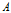 对训练数据集
对训练数据集
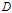 的信息增益
的信息增益
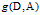 ,定义为集合
,定义为集合
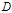 的经验熵
的经验熵
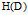 与特征A给定条件下
与特征A给定条件下
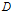 的经验条件熵
的经验条件熵
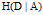 之差,即
之差,即
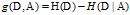
信息增益大的特征具有更强的分类能力
d.总结
给定训练数据集
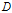 和特征
和特征
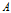 :
:
经验熵
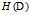 表示对数据集
表示对数据集
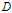 进行分类的不确定性
进行分类的不确定性
经验条件熵
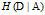 表示在特征
表示在特征
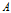 给定的条件下对数据集
给定的条件下对数据集
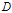 进行分类的不确定性
进行分类的不确定性
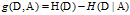 表示由于特征
表示由于特征
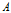 而使得对数据
而使得对数据
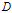 的分类的不确定性减少的程度。
的分类的不确定性减少的程度。
e.决策树进行分类的步骤
利用样本数据集构造一颗决策树,并通过构造的决策树建立相应的分类模型。这个过程实际上是从一个数据中获取知识,进行规制提炼的过程。
利用已经建立完成的决策树模型对数据集进行分类。即对未知的数据集元组从根节点依次进行决策树的游历,通过一定的路径游历至某叶子节点,从而找到该数据元组所在的类或类的分布。
三、示例
银行客户信用卡额度预测和判断
客户
信用记录
收入
年龄
工作性质
额度
C1
正常
较低
偏大
稳定
低
C2
正常
较低
偏大
一般
低
C3
良好
较低
偏大
稳定
高
C4
欠佳
普通
偏大
稳定
高
C5
欠佳
较高
正常
稳定
高
C6
欠佳
较高
正常
一般
低
C7
良好
较高
正常
一般
高
C8
正常
普通
偏大
稳定
低
C9
正常
较高
正常
稳定
高
C10
欠佳
普通
正常
稳定
高
C11
正常
普通
正常
一般
高
C12
良好
普通
偏大
一般
高
C13
良好
较低
正常
稳定
高
C14
欠佳
普通
偏大
一般
低
目标分类:信用卡额度:高=9,低=5
用来建立ID3决策树的客户情况的四个属性:
信用记录={良好、正常、欠佳}
收入={较低、普通、较高}
年龄={偏大、正常}
工作性质={稳定=8、一般=6}
ID3决策树的生成步骤
选择决策树的根节点,选着标准:根据属性的信息增益
节点属性划分
对划分的子集按照上述过程进行反复迭代来获得树的所有内部节点
最后根据节点、内部节点以及叶节点间的关系构建决策树
(1)计算分类属性'"额度"的熵
"额度"共有14条记录,其中高额度9条,低额度5条。
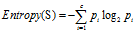
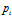 是类
是类
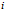 在
在
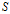 中的比例或概率。
中的比例或概率。
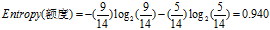
(2)计算各条件属性的熵
首先计算出不同属性值的熵:
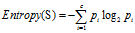
接着再计算整个属性的熵:
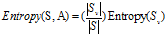
其中,
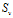 是
是
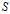 中属性
中属性
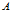 的值为
的值为
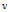 的子集,
的子集,
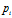 是类
是类
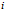 在
在
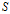 中的比例或概率。
中的比例或概率。
a."工作性质"的熵
稳定(wd):8=6高+2低
一般(yb):6=3高+3低
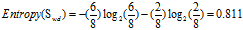
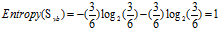
由"稳定"和一般"一般"的熵可求得属性"工作性质"的熵为:

b. 信用记录的熵
正常:5 =2高+3低
良好:4=4高+0低
欠佳:5=3高+2低
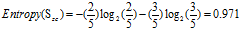
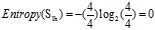
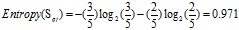
可得属性"信用记录"的熵为
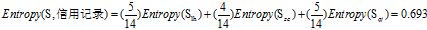
c."收入"的熵
较高:4=3高+1低
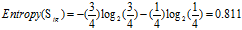
普通:6=4高+2低
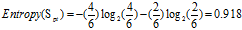
较低:4=2高+2低
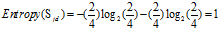
可得属性收入的熵为
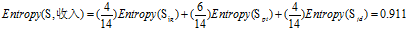
d."年龄"的熵
正常:7=6高+1低
偏大:7=3高+4低
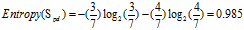
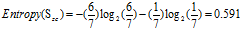
可得属性为"年龄"的熵:
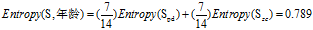
(3)计算各条件属性的增益
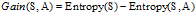 ,计算各个条件属性的增益
,计算各个条件属性的增益
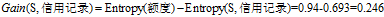
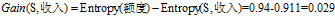
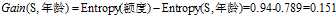
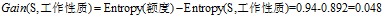
"信用记录"有着最大的增益,所以选择"信用记录"属性作为ID3决策树的根节点。
(4)计算和选择各分支节点
完成了根节点的选择后接下来选择各分支节点。因为"信用记录"有三种类型,所以根节点就有三个分支"良好","正常"和"欠佳",由于其中"良好"的熵为0就不考虑它了,只处理"正常"和"欠佳"
a."正常"分支节点的选择
"信用记录"为正常的有5条,
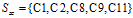 。通过之前的计算已经得到了"信用记录"为正常的熵:
。通过之前的计算已经得到了"信用记录"为正常的熵:
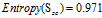 ,接着计算"信用记录"为正常的条件下各属性的熵
,接着计算"信用记录"为正常的条件下各属性的熵
客户
信用记录
收入
年龄
工作性质
额度
C1
正常
较低
偏大
稳定
低
C2
正常
较低
偏大
一般
低
C8
正常
普通
偏大
稳定
低
C9
正常
较高
正常
稳定
高
C11
正常
普通
正常
一般
高
(a)"收入"的熵
收入有三个属性值"较高"、"普通"和"较低",它们的熵分别为:
正常+较高:1=1高
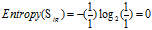
正常+普通:2 =1高+1低
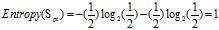
正常+较低:2=2低
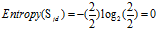
可得属性"收入"的熵:
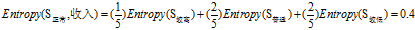
(b)"年龄"的熵
"年龄"={正常,偏大}
正常+正常:2=2高
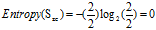
正常+偏大:3=3低
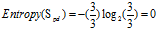
可得属性"年龄"的熵
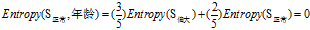
(c)"工作性质"的熵
"工作性质"={"一般","稳定"}
正常+一般:2=1高+1低
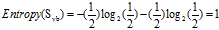
正常+稳定:3=1高+2低
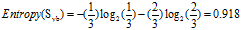
可得"工作性质"的熵
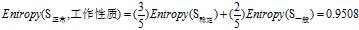
(d)计算
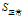 的各属性增益
的各属性增益
根据上面计算所得的熵值可以得到"信用记录"为"正常"的记录中其余三个属性的增益分别为:
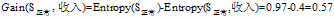
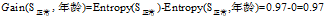
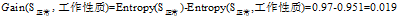
"年龄"在
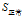 的三个属性中有着最大的增益,所以将"年龄"作为
的三个属性中有着最大的增益,所以将"年龄"作为
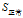 的分类点,又由于
的分类点,又由于
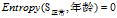 ,所以这一分支结束。
,所以这一分支结束。
b."欠佳"分支节点的选择
"信用记录"为"欠佳"的有
客户
信用记录
收入
年龄
工作性质
额度
C4
欠佳
普通
偏大
稳定
高
C5
欠佳
较高
正常
稳定
高
C6
欠佳
较高
正常
一般
低
C10
欠佳
普通
正常
稳定
高
C14
欠佳
普通
偏大
一般
低
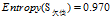
收入的熵
欠佳+较高:2=1高+1低
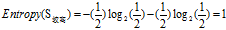
欠佳+普通:3=2高+1低
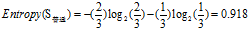
欠佳+较低:0
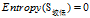
可得属性"收入"的熵为:
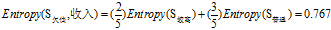
(b)"年龄"的熵
欠佳+正常 :3=2高+1低
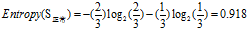
欠佳+偏大:2=1高+1低
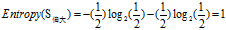
(c)"工作性质"的熵
欠佳+稳定: 3=3高
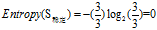
欠佳+一般:2=2低
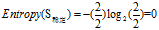
(d)计算
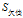 的各属性增益
的各属性增益
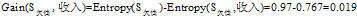
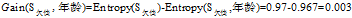
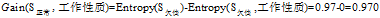
可以看到"工作性质"在
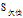 三个属性中有着最大的增益,所以将"工作性质"作为
三个属性中有着最大的增益,所以将"工作性质"作为
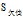 的分类节点
的分类节点
(5)生成叶节点
因为
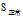 的"年龄"属性中"高"和"正常"的熵都为0,所以这一支的非叶节点划分结束,并以"低"和"高"作为"高"和"正常"分支的叶节点。
的"年龄"属性中"高"和"正常"的熵都为0,所以这一支的非叶节点划分结束,并以"低"和"高"作为"高"和"正常"分支的叶节点。
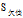 的"工作性质"中"一般"和"稳定"的熵为0,所以这一支的非叶节点也结束划分,并以"低"和高作为"一般"和"稳定"的分支的节点
的"工作性质"中"一般"和"稳定"的熵为0,所以这一支的非叶节点也结束划分,并以"低"和高作为"一般"和"稳定"的分支的节点
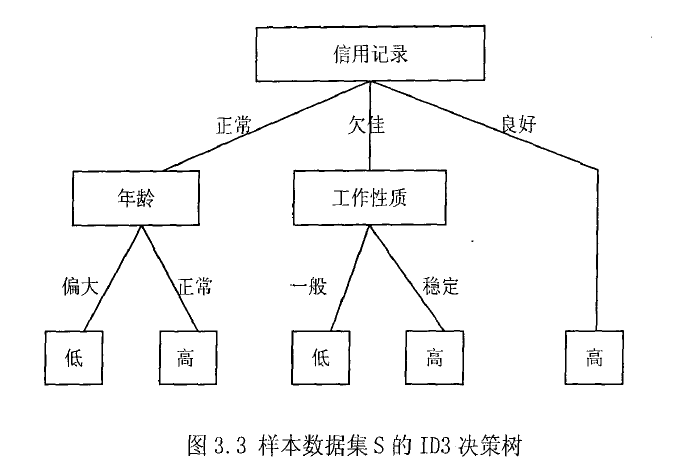
可得如下描述:
a, 如果"信用记录"为"正常"并且"年龄"偏大,那么授予的额度低
b, 如果"信用记录"为"正常"并且"年龄"正常,那么授予的额度高
c, 如果"信用记录"为"良好",那么授予额度高
d, 如果"信用记录"为"欠佳"并且"工作性质"一般,那么授予的额度低
e, 如果"信用记录"为"欠佳"并且"工作性质"稳定,那么授予的额度高
四、参考与致谢
1.李航《统计学习方法》
2.张睿《ID3决策树算法分析与改进》
这篇关于matlab 决策树分类调参,ID3决策树算法 - osc_dwi1do0o的个人空间 - OSCHINA - 中文开源技术交流社区...的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







