osc专题
STM32原理图一些引脚VDDA/VSSA/VBAT/OSC/NRST/BOOT
以STM32f103c8t6为例 OSC IN和OSC OUT引脚是STM32单片机上的外部高速晶体振荡器(crystal oscillator)的输入和输出引脚。这些引脚用于连接外部晶体振荡器,以提供精确的时钟信号给单片机,建立稳定的振荡回路。 OSC32_IN和OSC32_OUT引脚是STM32单片机上的外部32.768 kHz低速晶体振荡器的输入和输出引脚。这些引脚用于连接外部
本地代码提交到Git@OSC、github或其他远程仓库的方法
常规命令 git init touch README.md git add README.md git commit -m 'first commit'git remote add origin https://git.oschina.net/oschina/git-osc.git git push -u origin master 如果您在本地已经有需要上传到 Git@O
pt-osc 文档使用说明
pt-osc 文档使用说明 pt-osc 文档使用说明 功能介绍:工作原理:用法介绍举例 功能介绍: 在 alter 操作更改表结构的时候不⽤锁表,也就是说执⾏ alter 的时候不会阻塞 读写的操作 工作原理: 创建一个你要执alter操作的表⼀样的空表结构,执行表结构的修改,然后从 原表中 COPY 原始数据到表结构修改后的表,当数据 copy 完成以后就会将
OSC太原圈第二届技术交流会总结(8月3日)
2019独角兽企业重金招聘Python工程师标准>>> 题记:第二届技术交流会,我们又在美丽的太原理工大学(山西省唯一的“211工程”重点建设大学)内举行。此次,太原圈又注入了新鲜的力量,人数相比较上一届又多了近一倍。会场上,大家踊跃发言,群策群力!相信我们会越来越好! 2014年8月3号上午,天气虽然严热,却挡不住程序员们对知识的渴望 !一大早,大家从四面八方聚焦到太原理工大学! 有
3月16日 | openGauss与你相约OSC源创会·北京站
数据库技术已经发展了 60 多年,在数据量跃升、数据处理需求不断更迭的催化下,数据库类型也在多样化。从早期的关系型数据库,到如今大模型“带飞”的向量数据库,以及大热的分布式数据库,新型图数据库等等,各式数据库百花齐放,各有各的擅长场景。 对于开发者来说,数据库也是一个既有技术含量又有应用价值的领域。因此,OSCHINA 特别策划“数据库,2024 开炫”主题源创会,邀请不同类型的开源数据库齐
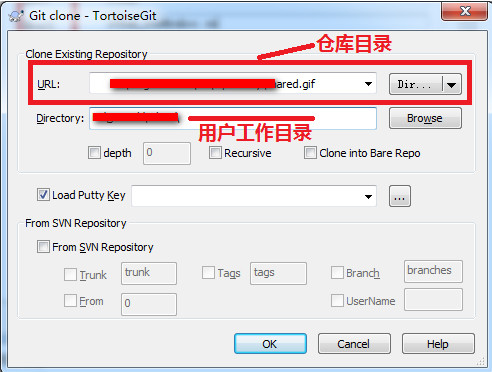
TortoiseGit配合msysGit在Git@OSC代码托管的傻瓜教程
自己的总结, 直接安装好git和TortoiseGit后,直接用几行命令就可以解决的事情. 大致内容是: 1, 在本地建立一个仓库. 2, 把服务器上的内容clone过来 3,add 4,Commit 5,push到远端服务器, 直接点击ok,当需要输入密码的时候, 输入即可. 点击ok后,发现此文件夹下多了一个隐藏的文件夹.git,则clone成功 如果你新建了一个项目,就建在刚刚
linux内核早期打印串口,内核启动早期的打印 - osc_ryjlu6z2的个人空间 - OSCHINA - 中文开源技术交流社区...
在移植4.16内核到tiny4412的过程中遇到一个问题,官方的uboot2012引导内核成功卡在staring the kernel没有了下文,看来内核还没有到注册uart驱动就已经挂掉了,尝试打开 early printk ,让内核自解压之后能够及时的打印信息。 说句题外话,内核启动卡在staring the kernel,在2440的时代,未使用设备树,这种情况往往是机器ID设置错误,或者
ReactNative重写的OSChina的Git@OSC客户端
http://git.oschina.net/rplees/react-native-gitosc 使用ReactNative仿造的Git@OSC! (感谢 xiekw2010) 更多截图 最近适配了Android 更多Android截图 扫描下载Android(如下载不了可以打开 发布连接 下载) Getting Started Require
eclipse的svn插件连接osc的代码仓库时候报错的解决办法
在使用eclipse的svn插件连接osc的代码仓库时候,发生了以下错误: Cannot negotiate authentication mechanism svn: Unable to connect to a repository at URL ‘svn://git.oschina.net/XXXXXX’ 但是用tortoisesvn可以正常连接。 eclipse的svn插件中,连
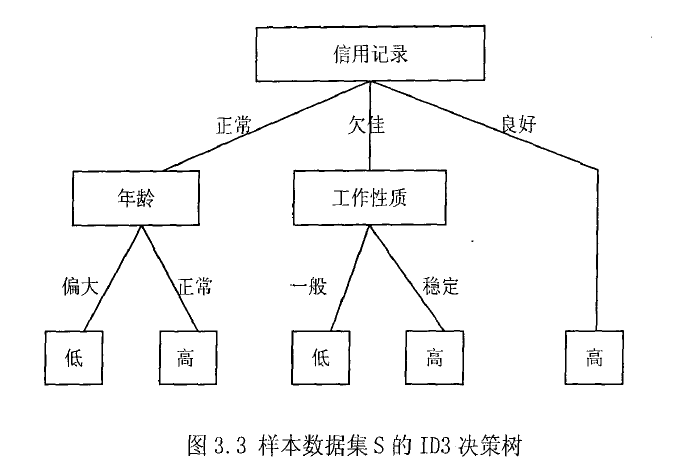
matlab 决策树分类调参,ID3决策树算法 - osc_dwi1do0o的个人空间 - OSCHINA - 中文开源技术交流社区...
一,简介 ID3(Iterative Dichotmizer 3) 1.什么是决策树学习 决策树学习是以训练或样本数据集为基础的归纳学习算法,是用于分类和预测的重要技术。 2.ID3核心思想 核心思想是利用信息熵原理选择信息增益最大的属性作为分类属性,递归地拓展决策树的分枝,完成决策树的构造 3.决策树学习本质是什么 决策树学习本质上是从训练数据集中归纳出一组分类规则 二,基础概念 a.信息熵
html应用样式p1,HTML光标样式 - osc_039ggp1i的个人空间 - OSCHINA - 中文开源技术交流社区...
把你的光标放到相应文字上鼠标显示效果 cursor:auto; 自动 cursor:zoom-in; 放大镜 cursor:zoom-out; 缩小镜 cursor:all-scroll; 上下左右任何方向滚动 cursor:crosshair; 十字准心 cursor:pointer; 手 cursor:wait; 等待 cursor:help; 帮助 cursor:no-drop; 无法释放
linux64栈帧,ARM栈帧与编译选项 - osc_tkri6ggp的个人空间 - OSCHINA - 中文开源技术交流社区...
看到一篇文章《冬之焱:谈谈Linux内核的栈回溯与妙用》,来自微信公众号"Linux阅码场"。文章主要写了Linux Backtrace的方法,里面提到ARM栈时,有这么一个图: 文章认为除了unwind模式,arm函数调用后都会压入PC,LR,SP,FP(即R15,R14,R13,R11)几个寄存器;但是,在平常ARM汇编代码中,很少能看到函数调用会压栈这么多寄存器。 实际上,压栈哪些寄存器
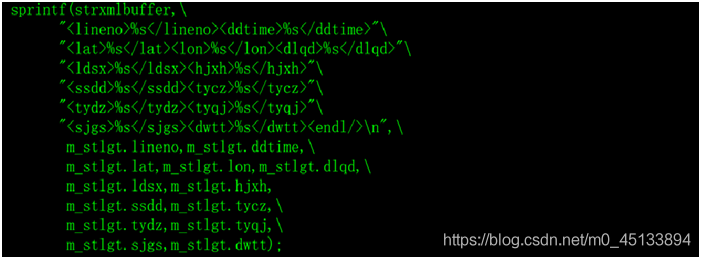
c语言abc 08 0,C语言格式化输出 - osc_oq0m8kxk的个人空间 - OSCHINA - 中文开源技术交流社区...
一、格式化输出 格式化输出的函数有printf、sprintf和snprintf等,功能略有不同,使用方法大同小异,本章节我们先以printf为例。 对于 printf 函数,相信大家并不陌生。之所以称它为格式化输出函数,该函数的声名如下: int printf(const char *format, ...) 大家看到printf函数的声明就会有点懵,它参数的写法与我们之前学到的函数知识不一样
p2在matlab中什么意思,Matlab入门笔记 - osc_299p2kiy的个人空间 - OSCHINA - 中文开源技术交流社区...
clear 清除变量; clc 擦黑板; 数据中的NaN代表非数,也就是不是数的意思。 matlab保留的keywords: (在命令行中输入iskeyword可打印) 以不同精度显示结果: 以long型显示(默认short): format long; 以科学计数法显示: format shortE; 行向
git@osc 简单教程
最近团队里面加入了几个小伙伴 @阔以编码的二胡选手、@十指秀, 为了能方便共同学习,我们准备开始写些东西出来。代码托管到 git@osc 上, 现在简单说下 git@osc 用法,其实它跟 git 的用法一样。 clone 大家都用过 svn ,这个 clone 就像 svn 中的 checkout 一样,将远程代码 拷贝到本地,并建立版本管理系统。具体用法如下: git clone htt
容斥原理公式c语言,【笔记】组合数学 - osc_3md1xrlp的个人空间 - OSCHINA - 中文开源技术交流社区...
开新坑辣。。。。。 排列组合 排列:P(n,r) = n! / (n-r)! 组合:C(n,r) = n! / r!(n-r)! 圆排列:P(n,r) / r 多重集排列: 令S是一个多重集,它有k个不同类型的元素,每一个元素都有无穷重复个数。那么S的r-排列的个数为k^r。 令S是一个多重集,它有k个不同类型的元素,各元素重数为n1,n2,...,nk。设S的大小为n = n1 + n2 +
High accuracy RC osc
本文提出了一种新型高性能低功耗的 RC 振荡器电路,该振荡电路结构简单,易于集成,并具有较高精度。通过少量调节电路,就可得到不同占空比的振荡波形。由于该电路的实现原理要求 RC 充放电时间远小于电容 C 两端电平的翻转时间,所以该电路的频率受到一定的限制。在对低频模拟集成电路或混合信号集成电路设计中,该电路具有非常广泛的应用。 1、VE变化缓慢,C点也不咋变化被钳位。 2、 R = 183.
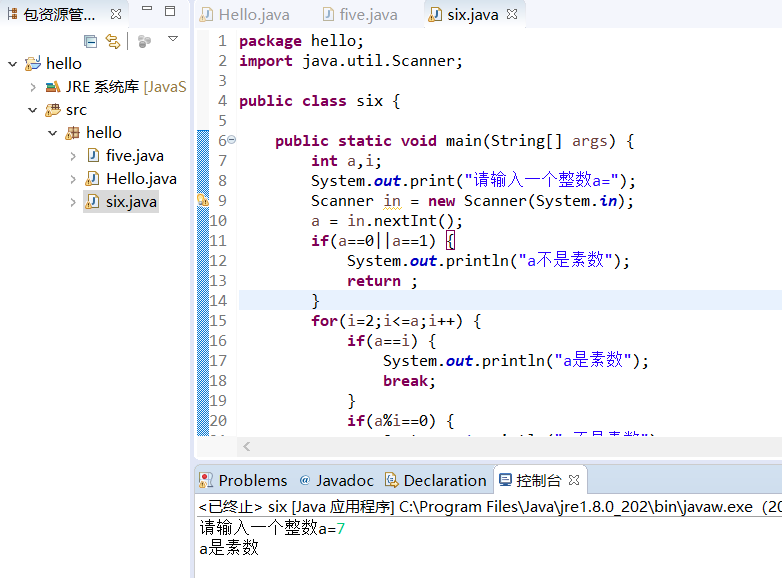
java第一次上机,Java第一次上机课 - osc_7luy07ds的个人空间 - OSCHINA - 中文开源技术交流社区...
1.编写程序: 声明一个整型变量a,并赋初值5,在程序中判断a是奇数还是偶数,然后输出判断的结果。 public class One { public static void main(String[] args) { int a=5; if(a%2==0){ System.out.println("偶数" ); }else{ System.out.println("奇数" ); } } }
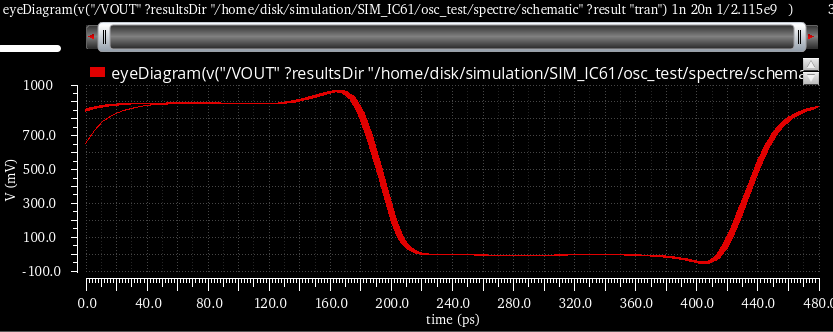
模拟仿真 OSC振荡器
用五个反相器做一个环形振荡器 跑瞬态仿真 发现并未振荡 手动添加起振 成功振荡 将上面的图像send to calculate,调用频率函数freq 可以看到振荡频率为2.5GHZ左右 如果想要降低振荡频率,可以在每个反相器后加寄生电容或者增大反相器尺寸,这里只演示增加寄生电容。 可以看到频率有所降低 可以查看每个反相器的输出端的波形,五
python莫比乌斯内接矩形_莫比乌斯反演部分习题 - osc_9uwqh9yn的个人空间 - OSCHINA - 中文开源技术交流社区...
最近写反演题也快没头了,各种线性不会筛,各种卡常…… 于是决定写一篇专题,来记录一下我写过的反演题目。 BZOJ1101: 求1<=i<=n,1<=j<=m,gcd(i,j)==d的对数。 先让n/=d,m/=d,变成求gcd(i,j)==1的对数。 然后预处理出μ(d)的前缀和,O(sqrt(n))枚举d即可。 代码: 1 #include 2 #include 3 #include 4
Git@OSC 开源中国git与sourceTree联合使用教程
Git@OSC 作为一个中国版的github,明显有着他自己的优势,比如速度快,汉语显示。sourcetree也可称得上是一个不错的git客户端,能够支持windows和mac os。本文就为这两者联合用来管理项目做一个入门的讲解。 准备工作 访问 https://git.oschina.net 注册一个账号;下载并安装sourceTree,这里是我上传的免积分下载的中文版 http://