机器学习算法系列（八）-对数几率回归算法（二）（Logistic Regression Algorithm）

本文主要是介绍机器学习算法系列（八）-对数几率回归算法（二）（Logistic Regression Algorithm），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

阅读本文需要的背景知识点：对数几率回归算法（一）、共轭梯度法、一点点编程知识

一、引言

接上一篇对数几率回归算法（一），其中介绍了优化对数几率回归代价函数的两种方法——梯度下降法（Gradient descent）与牛顿法（Newton’s method）。但当使用一些第三方机器学习库时会发现，一般都不会简单的直接使用上述两种方法，而是用的是一些优化版本或是算法的变体。例如前面介绍的在 scikit-learn 中可选的求解器如下表所示：

求解器/solver	算法
sag	随机平均梯度下降法（Stochastic Average Gradient/SAG）
saga	随机平均梯度下降加速法（SAGA）
lbfgs	L-BFGS算法（Limited-memory Broyden–Fletcher–Goldfarb–Shanno/L-BFGS）
newton-cg	牛顿-共轭梯度法（Newton-Conjugate Gradient）

下面就来一一介绍上述的这些算法，为什么一般第三方库中不直接梯度下降法与牛顿法，这两个原始算法存在什么缺陷？由于笔者能力有限，下面算法只给出了迭代公式，其迭代公式的来源无法在此详细推导出来，感兴趣的读者可参考对应论文中的证明。

二、梯度下降法

梯度下降法（Gradient Descent / GD）
梯度下降原始算法，也被称为批量梯度下降法（Batch gradient descent / BGD），将整个数据集作为输入来计算梯度。
$w=w-\eta \nabla_{w} \operatorname{Cost}(w)$

该算法的主要缺点是使用了整个数据集，当数据集很大的时候，计算梯度时可能会异常的耗时。

随机梯度下降法（Stochastic Gradient Descent / SGD）
每次迭代更新只随机的处理某一个数据，而不是整个数据集。
$w=w-\eta \nabla_{w} \operatorname{Cost}\left(w, X_{i}, y_{i}\right) \quad i \in[1, N]$

该算法由于是随机一个数据点，代价函数并不是一直下降，而是会上下波动，调整步长使得代价函数的结果整体呈下降趋势，所以收敛速率没有批量梯度下降快。

小批量梯度下降法（Mini-batch Gradient Descent / MBGD）
小批量梯度下降法结合了上面两种算法，在计算梯度是既不是使用整个数据集，也不是每次随机选其中一个数据，而是一次使用一部分数据来更新。
$w=w-\eta \nabla_{w} \operatorname{Cost}\left(w, X_{(i: i+k)}, y_{(i: i+k)}\right) \quad i \in[1, N]$

随机平均梯度下降法¹（Stochastic Average Gradient / SAG）
随机平均梯度下降法是对随机梯度下降法的优化，由于 SGD 的随机性，导致其收敛速度较缓慢。SAG 则是通过记录上一次位置的梯度记录，使得能够看到更多的信息。
$\begin{aligned} w_{k+1} &=w_{k}-\frac{\eta}{N} \sum_{i=1}^{N}\left(d_{i}\right)_{k} \\ d_{k} &=\left\{\begin{array}{ll} \nabla_{w} \operatorname{Cost}\left(w_{k}, X_{i}, y_{i}\right) & i=i_{k} \\ d_{k-1} & i \neq i_{k} \end{array}\right. \end{aligned}$

方差缩减随机梯度下降法²（Stochastic Variance Reduced Gradient / SVRG）
方差缩减随机梯度下降法是对随机梯度下降法的另一种优化，由于 SGD 的收敛问题是由于梯度的方差假设有一个常数的上界，SVRG 的做法是通过减小这个方差来使得收敛过程更加稳定。
$w_{k+1}=w_{k}-\eta\left(\nabla_{w} \operatorname{Cost}\left(w_{k}, X_{i}, y_{i}\right)-\nabla_{w} \operatorname{Cost}\left(\hat{w}, X_{i}, y_{i}\right)+\frac{1}{N} \sum_{j=1}^{N} \nabla_{w} \operatorname{Cost}\left(\hat{w}, X_{j}, y_{j}\right)\right)$

随机平均梯度下降法变体³（SAGA）
SAGA 是对随机平均梯度下降法的优化，结合了方差缩减随机梯度下降法的方法。
$w_{k+1}=w_{k}-\eta\left(\nabla_{w} \operatorname{Cost}\left(w_{k}, X_{i}, y_{i}\right)-\nabla_{w} \operatorname{Cost}\left(w_{k-1}, X_{i}, y_{i}\right)+\frac{1}{N} \sum_{j=1}^{N} \nabla_{w} \operatorname{Cost}\left(w, X_{j}, y_{j}\right)\right)$

三、牛顿法

牛顿法（Newton Method）
牛顿法原始版本，将整个数据集作为输入来计算出梯度和黑塞矩阵后求出下降的方向
$w_{k+1}=w_{k}-\eta\left(H^{-1} \nabla_{w} \operatorname{Cost}\left(w_{k}\right)\right)$

该算法的主要缺点是需要求黑塞矩阵和它的逆矩阵，当 x 的维度过多的时候，求黑塞矩阵的过程会异常的困难。

DFP法⁴（Davidon–Fletcher–Powell）
DFP 法是一个拟牛顿法，算法如下：
$\begin{aligned} g_{k} &=\nabla_{w} \operatorname{Cost}\left(w_{k}\right) \\ d_{k} &=-D_{k} g_{k} \\ s_{k} &=\eta d_{k} \\ w_{k+1} &=w_{k}+s_{k} \\ g_{k+1} &=\nabla_{w} \operatorname{Cost}\left(w_{k+1}\right) \\ y_{k} &=g_{k+1}-g_{k} \\ D_{k+1} &=D_{k}+\frac{s_{k} s_{k}^{T}}{s_{k}^{T} y_{k}}-\frac{D_{k} y_{k} y_{k}^{T} D_{K}}{y_{k}^{T} D_{k} y_{k}} \end{aligned}$

可以看到 DFP 不再直接求黑塞矩阵，而是通过一次一次的迭代来得到近似值，其中 D 为黑塞矩阵的逆矩阵的近似。

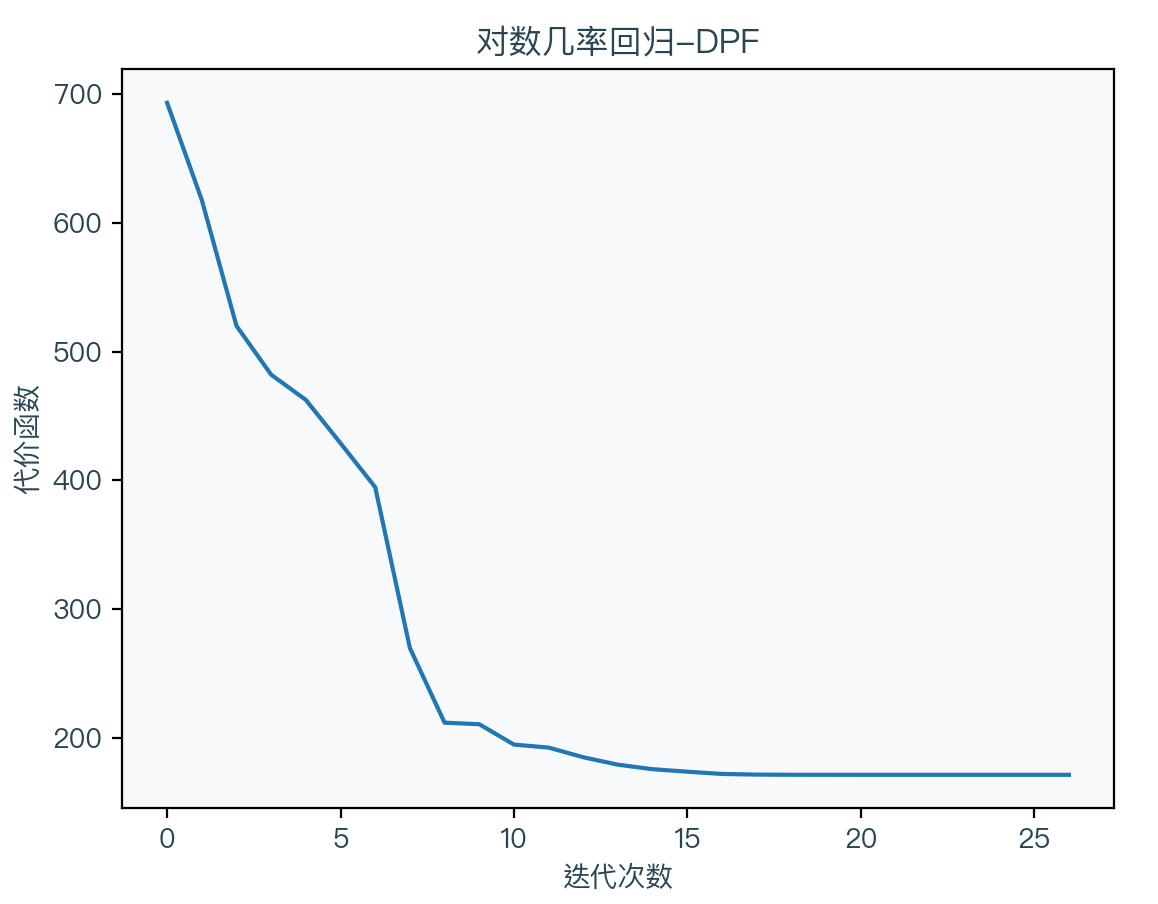
BFGS法⁵（Broyden–Fletcher–Goldfarb–Shanno）
BFGS 法同样是一个拟牛顿法，基本步骤与 DFP 法一模一样，算法如下：
$\begin{aligned} g_{k} &=\nabla_{w} \operatorname{Cost}\left(w_{k}\right) \\ d_{k} &=-D_{k} g_{k} \\ s_{k} &=\eta d_{k} \\ w_{k+1} &=w_{k}+s_{k+1} \\ g_{k+1} &=\nabla_{w} \operatorname{Cost}\left(w_{k+1}\right) \\ y_{k} &=g_{k+1}-g_{k} \\ D_{k+1} &=\left(I-\frac{s_{k} y_{k}^{T}}{y_{k}^{T} s_{k}}\right) D_{k}\left(I-\frac{y_{k} s_{k}^{T}}{y_{k}^{T} s_{k}}\right)+\frac{s_{k} s_{k}^{T}}{y_{k}^{T} s_{k}} \end{aligned}$

可以看到 BFGS 法的唯一区别只是对黑塞矩阵的近似方法不同，其中 D 为黑塞矩阵的逆矩阵的近似。

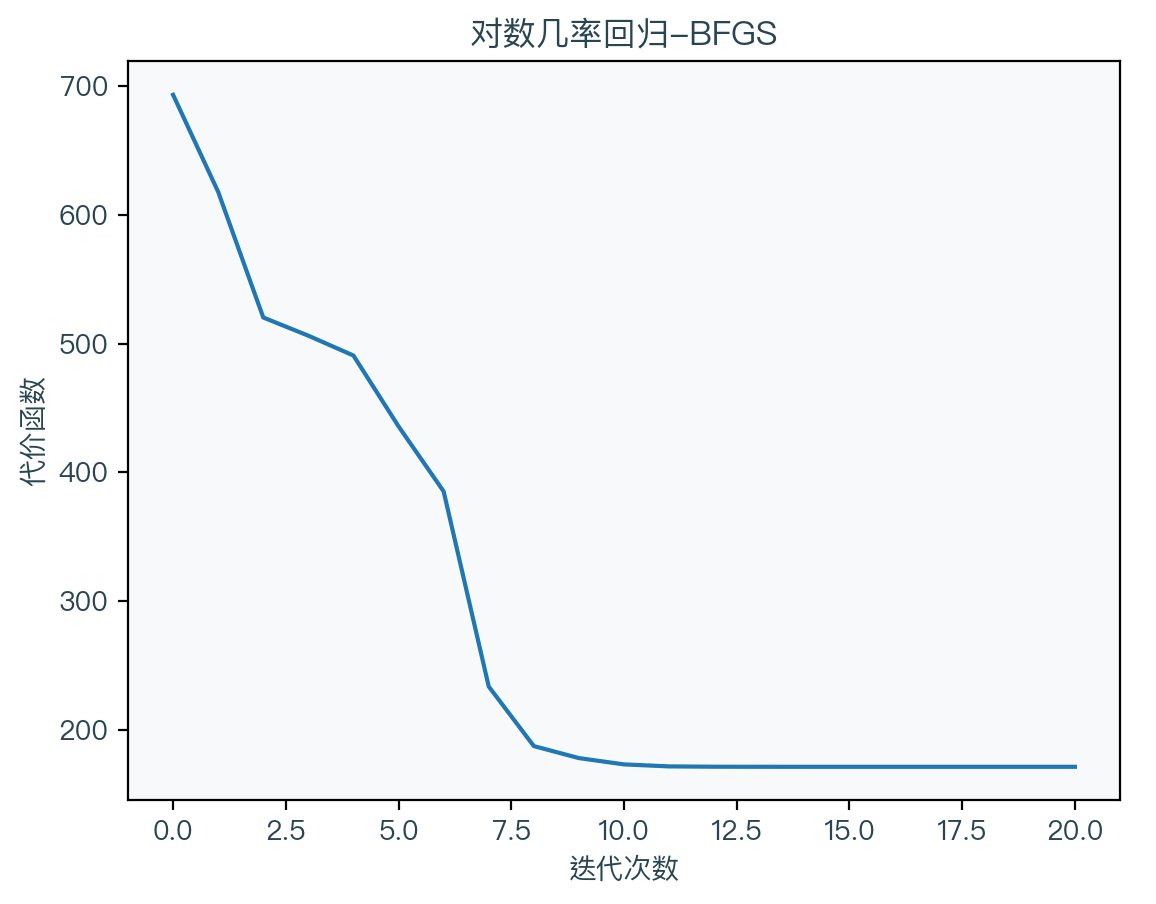
L-BFGS法⁶（Limited-memory Broyden–Fletcher–Goldfarb–Shanno）
由于 BFGS 法需要存储一个近似的黑塞矩阵，当 x 的维度过多的时候，这个黑塞矩阵的占用内存会异常的大，L-BFGS 法则是对 BFGS 法再一次的近似，算法如下：
$\begin{aligned} g_{k} &=\nabla_{w} \operatorname{Cost}\left(w_{k}\right) \\ d_{k} &=-\operatorname{calcDirection}\left(s_{k-m: k-1}, y_{k-m: k-1}, \rho_{k-m: k-1}, g_{k}\right) \\ s_{k} &=\eta d_{k} \\ w_{k+1} &=w_{k}+s_{k} \\ g_{k+1} &=\nabla_{w} \operatorname{Cost}\left(w_{k+1}\right) \\ y_{k} &=g_{k+1}-g_{k} \\ \rho_{k} &=\frac{1}{y_{k}^{T} s_{k}} \end{aligned}$

可以看到 L-BFGS 法不再直接保存这个近似的黑塞矩阵，而是当要用到时直接通过一组向量计算出来，达到节省内存的目的。计算方向的方法可参考下面代码中的实现。

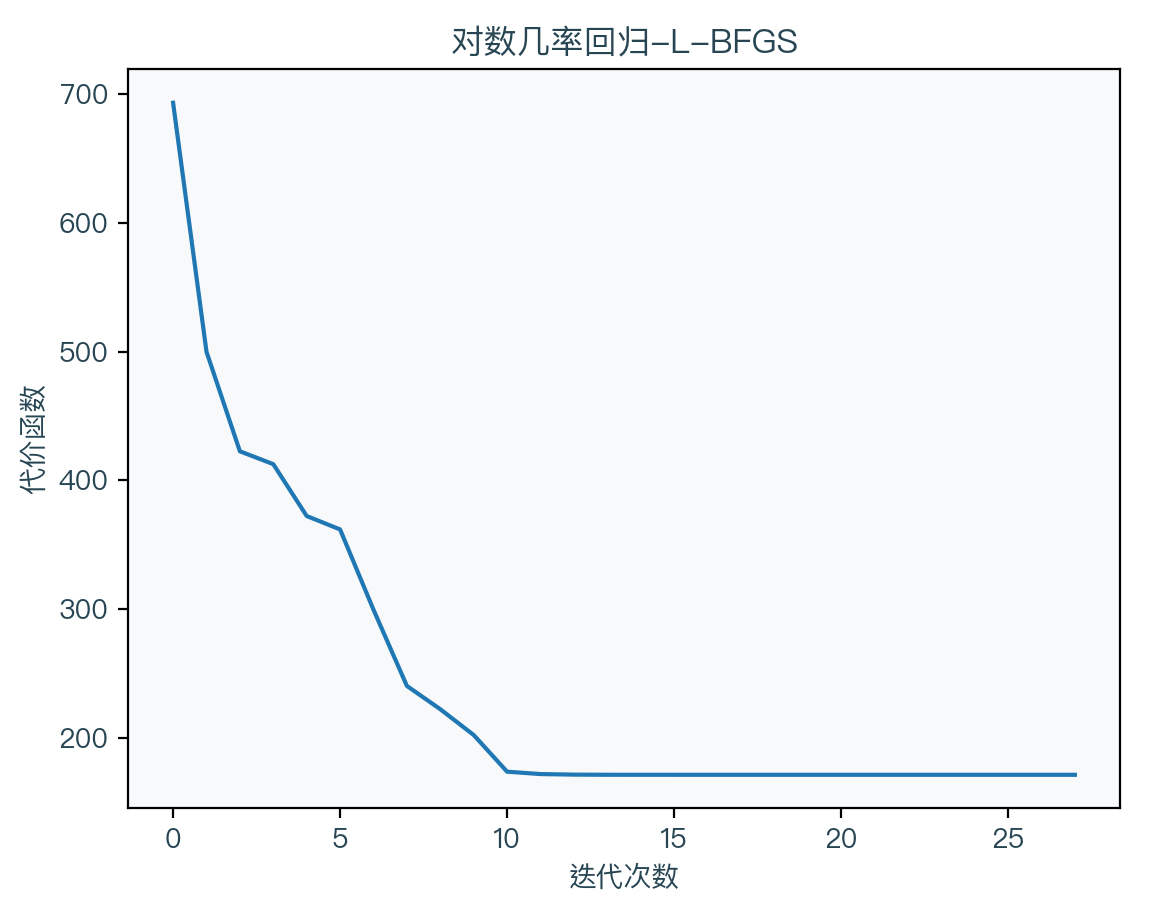
牛顿共轭梯度法（Newton-Conjugate Gradient / Newton-CG）
牛顿共轭梯度法是对牛顿法的优化，算法如下：
$\begin{aligned} g_{k} &=\nabla_{w} \operatorname{Cost}\left(w_{k}\right) \\ H_{k} &=\nabla_{w}^{2} \operatorname{Cost}\left(w_{k}\right) \\ \Delta w &=c g\left(g_{k}, H_{k}\right) \\ w_{k+1} &=w_{k}-\Delta w \end{aligned}$

可以看到牛顿共轭梯度法不再求黑塞矩阵的逆矩阵，而是通过共轭梯度法（Conjugate Gradient）直接求出 Δw。关于共轭梯度法推荐看参考文献中的文章⁷，详细介绍了该算法的原理与应用。

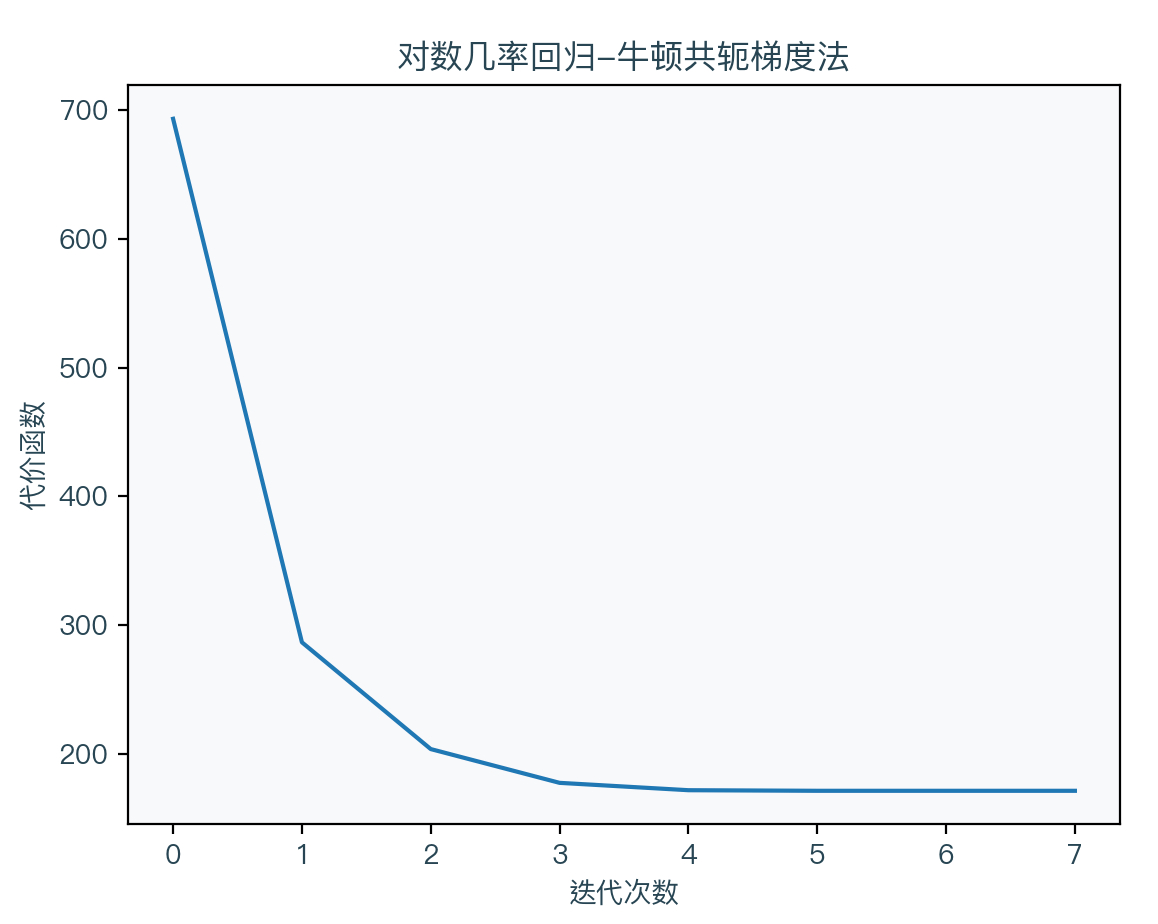
四、代码实现

使用 Python 实现对数几率回归算法（随机梯度下降法）：

import numpy as npdef logisticRegressionSGD(X, y, max_iter=100, tol=1e-4, step=1e-1):w = np.zeros(X.shape[1])xy = np.c_[X.reshape(X.shape[0], -1), y.reshape(X.shape[0], 1)]for it in range(max_iter):s = step / (np.sqrt(it + 1))np.random.shuffle(xy)X_new, y_new = xy[:, :-1], xy[:, -1:].ravel()for i in range(0, X.shape[0]):d = dcost(X_new[i], y_new[i], w)if (np.linalg.norm(d) <= tol):return ww = w - s * dreturn w

使用 Python 实现对数几率回归算法（批量随机梯度下降法）：

import numpy as npdef logisticRegressionMBGD(X, y, batch_size=50, max_iter=100, tol=1e-4, step=1e-1):w = np.zeros(X.shape[1])xy = np.c_[X.reshape(X.shape[0], -1), y.reshape(X.shape[0], 1)]for it in range(max_iter):s = step / (np.sqrt(it + 1))np.random.shuffle(xy)for start in range(0, X.shape[0], batch_size):stop = start + batch_sizeX_batch, y_batch = xy[start:stop, :-1], xy[start:stop, -1:].ravel()d = dcost(X_batch, y_batch, w)if (np.linalg.norm(p_avg) <= tol):return ww = w - s * dreturn w

使用 Python 实现对数几率回归算法（随机平均梯度下降法）：

import numpy as npdef logisticRegressionSAG(X, y, max_iter=100, tol=1e-4, step=1e-1):w = np.zeros(X.shape[1])p = np.zeros(X.shape[1])d_prev = np.zeros(X.shape)for it in range(max_iter):s = step / (np.sqrt(it + 1))for it in range(X.shape[0]):i = np.random.randint(0, X.shape[0])d = dcost(X[i], y[i], w)p = p - d_prev[i] + dd_prev[i] = dp_avg = p / X.shape[0]if (np.linalg.norm(p_avg) <= tol):return ww = w - s * p_avgreturn w

使用 Python 实现对数几率回归算法（方差缩减随机梯度下降法）：

import numpy as npdef logisticRegressionSVRG(X, y, max_iter=100, m = 100, tol=1e-4, step=1e-1):w = np.zeros(X.shape[1])for it in range(max_iter):s = step / (np.sqrt(it + 1))g = np.zeros(X.shape[1])for i in range(X.shape[0]): g = g + dcost(X[i], y[i], w)g = g / X.shape[0]tempw = wfor it in range(m):i = np.random.randint(0, X.shape[0])d_tempw = dcost(X[i], y[i], tempw)d_w = dcost(X[i], y[i], w)d = d_tempw - d_w + gif (np.linalg.norm(d) <= tol):breaktempw = tempw - s * dw = tempwreturn w

使用 Python 实现对数几率回归算法（SAGA）：

import numpy as npdef logisticRegressionSAGA(X, y, max_iter=100, tol=1e-4, step=1e-1):w = np.zeros(X.shape[1])p = np.zeros(X.shape[1])d_prev = np.zeros(X.shape)for i in range(X.shape[0]): d_prev[i] = dcost(X[i], y[i], w)for it in range(max_iter):s = step / (np.sqrt(it + 1))for it in range(X.shape[0]):i = np.random.randint(0, X.shape[0])d = dcost(X[i], y[i], w)p = d - d_prev[i] + np.mean(d_prev, axis=0) d_prev[i] = dif (np.linalg.norm(p) <= tol):return ww = w - s * preturn w

使用 Python 实现对数几率回归算法（DFP）：

import numpy as npdef logisticRegressionDPF(X, y, max_iter=100, tol=1e-4):w = np.zeros(X.shape[1])D_k = np.eye(X.shape[1])g_k = dcost(X, y, w)for it in range(max_iter):d_k = -D_k.dot(g_k)s = lineSearch(X, y, w, d_k, 0, 10)s_k = s * d_kw = w + s_kg_k_1 = dcost(X, y, w)if (np.linalg.norm(g_k_1) <= tol):return wy_k = (g_k_1 - g_k).reshape(-1, 1)s_k = s_k.reshape(-1, 1)D_k = D_k + s_k.dot(s_k.T) / s_k.T.dot(y_k) - D_k.dot(y_k).dot(y_k.T).dot(D_k) / y_k.T.dot(D_k).dot(y_k)g_k = g_k_1return w

使用 Python 实现对数几率回归算法（BFGS）：

import numpy as npdef logisticRegressionBFGS(X, y, max_iter=100, tol=1e-4):w = np.zeros(X.shape[1])D_k = np.eye(X.shape[1])g_k = dcost(X, y, w)for it in range(max_iter):d_k = -D_k.dot(g_k)s = lineSearch(X, y, w, d_k, 0, 10)s_k = s * d_kw = w + s_kg_k_1 = dcost(X, y, w)if (np.linalg.norm(g_k_1) <= tol):return wy_k = (g_k_1 - g_k).reshape(-1, 1)s_k = s_k.reshape(-1, 1)a = s_k.dot(y_k.T)b = y_k.T.dot(s_k)c = s_k.dot(s_k.T)D_k = (np.eye(X.shape[1]) - a / b).dot(D_k).dot((np.eye(X.shape[1]) - a.T / b)) + c / bg_k = g_k_1return w

使用 Python 实现对数几率回归算法（L-BFGS）：

import numpy as npdef calcDirection(ss, ys, rhos, g_k, m, k):delta = 0L = kq = g_k.reshape(-1, 1)if k > m:delta = k - mL = malphas = np.zeros(L)for i in range(L - 1, -1, -1):j = i + deltaalpha = rhos[j].dot(ss[j].T).dot(q)alphas[i] = alphaq = q - alpha * ys[j]r = np.eye(g_k.shape[0]).dot(q)for i in range(0, L):j = i + deltabeta = rhos[j].dot(ys[j].T).dot(r)r = r + (alphas[i] - beta) * ss[j]return -r.ravel()def logisticRegressionLBFGS(X, y, m=100, max_iter=100, tol=1e-4):w = np.zeros(X.shape[1])g_k = dcost(X, y, w)d_k = -np.eye(X.shape[1]).dot(g_k)ss = []ys = []rhos = []for it in range(max_iter):d_k = calcDirection(ss, ys, rhos, g_k, m, it)s = lineSearch(X, y, w, d_k, 0, 1)s_k = s * d_kw = w + s_kg_k_1 = dcost(X, y, w)if (np.linalg.norm(g_k_1) <= tol):return wy_k = (g_k_1 - g_k).reshape(-1, 1)s_k = s_k.reshape(-1, 1)ss.append(s_k)ys.append(y_k)rhos.append(1 / (y_k.T.dot(s_k)))g_k = g_k_1return w

使用 Python 实现对数几率回归算法（牛顿共轭梯度法）：

import numpy as npdef cg(H, g, max_iter=100, tol=1e-4):"""共轭梯度法H * deltaw = g"""deltaw = np.zeros(g.shape[0])i = 0r = gd = rdelta = np.dot(r, r)delta_0 = deltawhile i < max_iter:q = H.dot(d)alpha = delta / (np.dot(d, q))deltaw = deltaw + alpha * dr = r - alpha * qdelta_prev = deltadelta = np.dot(r, r)if delta <= tol * tol * delta_0:breakbeta = delta / delta_prevd = r + beta * di = i + 1return deltawdef logisticRegressionNewtonCG(X, y, max_iter=100, tol=1e-4, step = 1.0):"""对数几率回归，使用牛顿共轭梯度法（Newton-Conjugate Gradient）args:X - 训练数据集y - 目标标签值max_iter - 最大迭代次数tol - 变化量容忍值return:w - 权重系数"""# 初始化 w 为零向量w = np.zeros(X.shape[1])# 开始迭代for it in range(max_iter):# 计算梯度d = dcost(X, y, w)# 当梯度足够小时，结束迭代if np.linalg.norm(d) <= tol:break# 计算黑塞矩阵H = ddcost(X, y, w)# 使用共轭梯度法计算Δw deltaw = cg(H, d)w = w - step * deltawreturn w

五、第三方库实现

scikit-learn⁸ 实现对数几率回归（随机平均梯度下降法）：

from sklearn.linear_model import LogisticRegression# 初始化对数几率回归器，无正则化
reg = LogisticRegression(penalty="none", solver="sag")
# 拟合线性模型
reg.fit(X, y)
# 权重系数
w = reg.coef_
# 截距
b = reg.intercept_

scikit-learn⁸实现对数几率回归（SAGA）：

from sklearn.linear_model import LogisticRegression# 初始化对数几率回归器，无正则化
reg = LogisticRegression(penalty="none", solver="saga")
# 拟合线性模型
reg.fit(X, y)
# 权重系数
w = reg.coef_
# 截距
b = reg.intercept_

scikit-learn⁸实现对数几率回归（L-BFGS）：

from sklearn.linear_model import LogisticRegression# 初始化对数几率回归器，无正则化
reg = LogisticRegression(penalty="none", solver="lbfgs")
# 拟合线性模型
reg.fit(X, y)
# 权重系数
w = reg.coef_
# 截距
b = reg.intercept_

scikit-learn⁸实现对数几率回归（牛顿共轭梯度法）：

from sklearn.linear_model import LogisticRegression# 初始化对数几率回归器，无正则化
reg = LogisticRegression(penalty="none", solver="newton-cg")
# 拟合线性模型
reg.fit(X, y)
# 权重系数
w = reg.coef_
# 截距
b = reg.intercept_

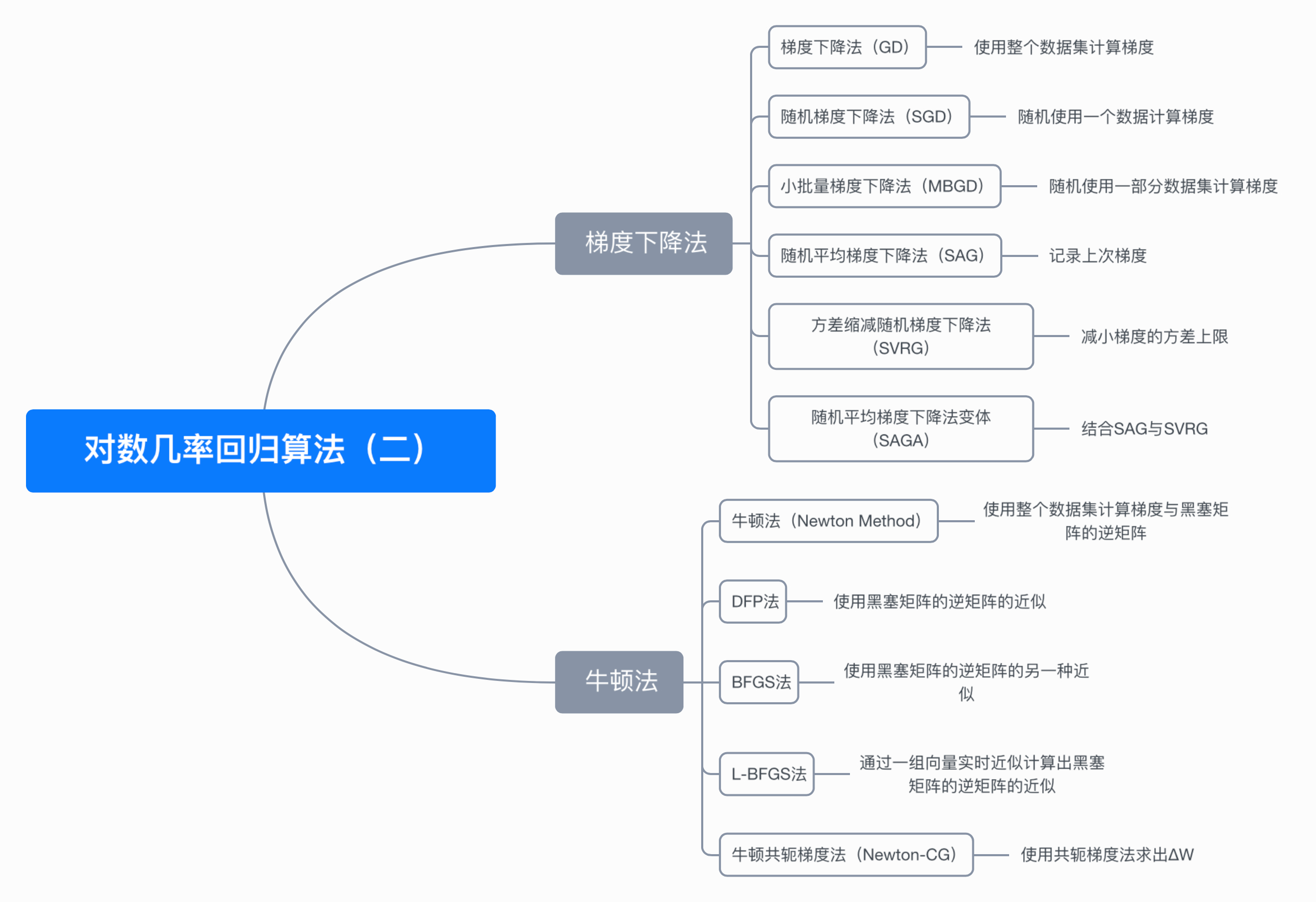
七、思维导图

八、参考文献

https://hal.inria.fr/hal-00860051/document
https://harkiratbehl.github.io/projects/svrg/svrg.pdf
https://arxiv.org/pdf/1407.0202.pdf
https://en.wikipedia.org/wiki/Davidon%E2%80%93Fletcher%E2%80%93Powell_formula
https://en.wikipedia.org/wiki/Broyden%E2%80%93Fletcher%E2%80%93Goldfarb%E2%80%93Shanno_algorithm
https://en.wikipedia.org/wiki/Limited-memory_BFGS
https://flat2010.github.io/2018/10/26/%E5%85%B1%E8%BD%AD%E6%A2%AF%E5%BA%A6%E6%B3%95%E9%80%9A%E4%BF%97%E8%AE%B2%E4%B9%89/#B2-%E5%85%B1%E8%BD%AD%E6%A2%AF%E5%BA%A6%E7%AE%97%E6%B3%95
https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html

完整演示请点击这里

注：本文力求准确并通俗易懂，但由于笔者也是初学者，水平有限，如文中存在错误或遗漏之处，恳请读者通过留言的方式批评指正

本文首发于——AI导图，欢迎关注

这篇关于机器学习算法系列（八）-对数几率回归算法（二）（Logistic Regression Algorithm）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！