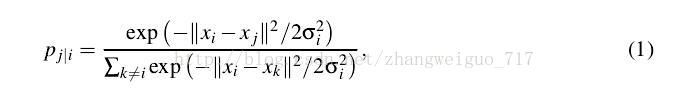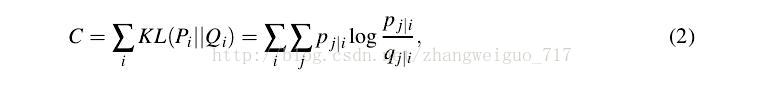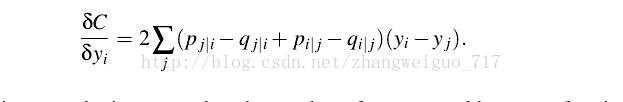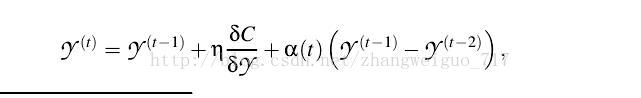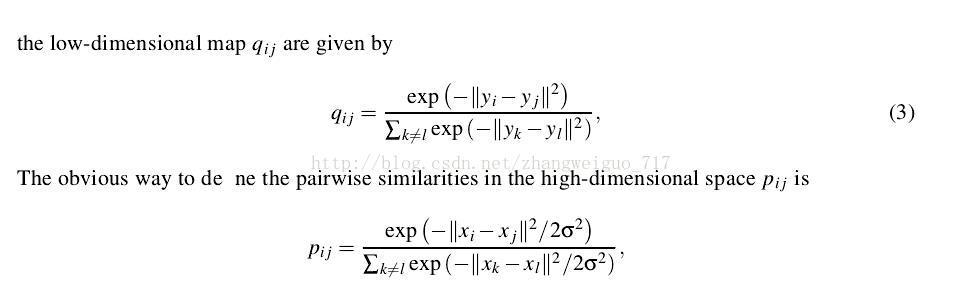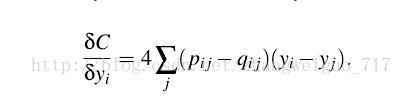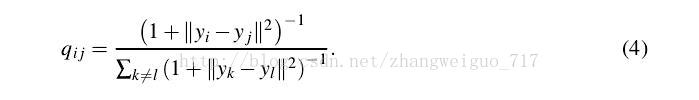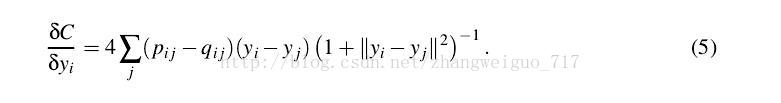【机器学习】降维算法 PCA、LDA、LLE、Laplacian EigenmapsI、SOMAP 、 MDS、SNE、TSNE

本文主要是介绍【机器学习】降维算法 PCA、LDA、LLE、Laplacian EigenmapsI、SOMAP 、 MDS、SNE、TSNE，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

机器学习领域中所谓的降维就是指采用某种映射方法，将原高维空间中的数据点映射到低维度的空间中。降维的本质是学习一个映射函数 f : x->y，其中x是原始数据点的表达，目前最多使用向量表达形式。 y是数据点映射后的低维向量表达，通常y的维度小于x的维度（当然提高维度也是可以的）。f可能是显式的或隐式的、线性的或非线性的。

目前大部分降维算法处理向量表达的数据，也有一些降维算法处理高阶张量表达的数据。之所以使用降维后的数据表示是因为在原始的高维空间中，包含有冗余信息以及噪音信息，在实际应用例如图像识别中造成了误差，降低了准确率；而通过降维,我们希望减少冗余信息所造成的误差,提高识别（或其他应用）的精度。又或者希望通过降维算法来寻找数据内部的本质结构特征。

在很多算法中，降维算法成为了数据预处理的一部分，如PCA。事实上，有一些算法如果没有降维预处理，其实是很难得到很好的效果的。

主成分分析算法（PCA）

Principal Component Analysis(PCA)是最常用的线性降维方法，它的目标是通过某种线性投影，将高维的数据映射到低维的空间中表示，并期望在所投影的维度上数据的方差最大，以此使用较少的数据维度，同时保留住较多的原数据点的特性。

通俗的理解，如果把所有的点都映射到一起，那么几乎所有的信息（如点和点之间的距离关系）都丢失了，而如果映射后方差尽可能的大，那么数据点则会分散开来，以此来保留更多的信息。可以证明，PCA是丢失原始数据信息最少的一种线性降维方式。（实际上就是最接近原始数据，但是PCA并不试图去探索数据内在结构）

设n维向量w为目标子空间的一个坐标轴方向（称为映射向量），最大化数据映射后的方差，有：

其中m是数据实例的个数， xi是数据实例i的向量表达， x拔是所有数据实例的平均向量。定义W为包含所有映射向量为列向量的矩阵，经过线性代数变换，可以得到如下优化目标函数：

其中tr表示矩阵的迹，A是数据协方差矩阵。

容易得到最优的W是由数据协方差矩阵前k个最大的特征值对应的特征向量作为列向量构成的。这些特征向量形成一组正交基并且最好地保留了数据中的信息。

PCA的输出就是Y = W‘X，由X的原始维度降低到了k维。

 

PCA追求的是在降维之后能够最大化保持数据的内在信息，并通过衡量在投影方向上的数据方差的大小来衡量该方向的重要性。但是这样投影以后对数据的区分作用并不大，反而可能使得数据点揉杂在一起无法区分。这也是PCA存在的最大一个问题，这导致使用PCA在很多情况下的分类效果并不好。具体可以看下图所示，若使用PCA将数据点投影至一维空间上时，PCA会选择2轴，这使得原本很容易区分的两簇点被揉杂在一起变得无法区分；而这时若选择1轴将会得到很好的区分结果。

 

Discriminant Analysis所追求的目标与PCA不同，不是希望保持数据最多的信息，而是希望数据在降维后能够很容易地被区分开来。后面会介绍LDA的方法，是另一种常见的线性降维方法。另外一些非线性的降维方法利用数据点的局部性质，也可以做到比较好地区分结果，例如LLE，Laplacian Eigenmap等。以后会介绍。

LDA

Linear Discriminant Analysis (也有叫做Fisher Linear Discriminant)是一种有监督的（supervised）线性降维算法。与PCA保持数据信息不同，LDA是为了使得降维后的数据点尽可能地容易被区分！

假设原始数据表示为X，（m*n矩阵，m是维度，n是sample的数量）

既然是线性的，那么就是希望找到映射向量a， 使得 a‘X后的数据点能够保持以下两种性质：

1、同类的数据点尽可能的接近（within class）

2、不同类的数据点尽可能的分开（between class）

所以呢还是上次PCA用的这张图，如果图中两堆点是两类的话，那么我们就希望他们能够投影到轴1去（PCA结果为轴2），这样在一维空间中也是很容易区分的。

接下来是推导，因为这里写公式很不方便，我就引用Deng Cai老师的一个ppt中的一小段图片了：

思路还是非常清楚的，目标函数就是最后一行J（a)，μ（一飘）就是映射后的中心用来评估类间距，s（一瓢）就是映射后的点与中心的距离之和用来评估类内距。J(a)正好就是从上述两个性质演化出来的。

因此两类情况下：

加上a’a=1的条件（类似于PCA）

可以拓展成多类：

以上公式推导可以具体参考pattern classification书中的相应章节，讲fisher discirminant的

OK，计算映射向量a就是求最大特征向量，也可以是前几个最大特征向量组成矩阵A=[a1,a2,….ak]之后，就可以对新来的点进行降维了：y = A’X（线性的一个好处就是计算方便！）

可以发现，LDA最后也是转化成为一个求矩阵特征向量的问题，和PCA很像，事实上很多其他的算法也是归结于这一类，一般称之为谱（spectral）方法。

线性降维算法我想最重要的就是PCA和LDA了，后面还会介绍一些非线性的方法。

LLE 局部线性嵌入

Locally linear embedding（LLE）[1] 是一种非线性降维算法，它能够使降维后的数据较好地保持原有流形结构。LLE可以说是流形学习方法最经典的工作之一。很多后续的流形学习、降维方法都与LLE有密切联系。

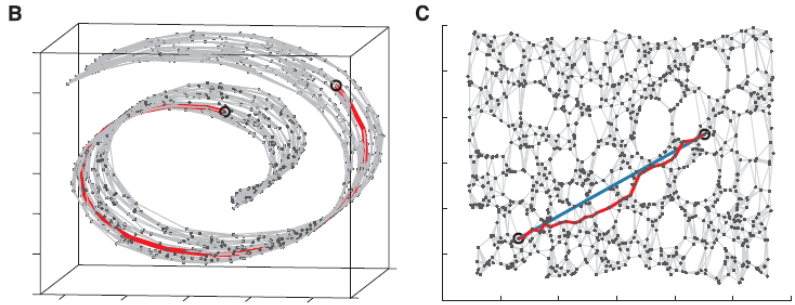
见图1，使用LLE将三维数据（b）映射到二维（c）之后，映射后的数据仍能保持原有的数据流形（红色的点互相接近，蓝色的也互相接近），说明LLE有效地保持了数据原有的流行结构。

但是LLE在有些情况下也并不适用，如果数据分布在整个封闭的球面上，LLE则不能将它映射到二维空间，且不能保持原有的数据流形。那么我们在处理数据中，首先假设数据不是分布在闭合的球面或者椭球面上。

 

图1 LLE降维算法使用实例

LLE算法认为每一个数据点都可以由其近邻点的线性加权组合构造得到。算法的主要步骤分为三步：(1)寻找每个样本点的k个近邻点；（2）由每个样本点的近邻点计算出该样本点的局部重建权值矩阵；（3）由该样本点的局部重建权值矩阵和其近邻点计算出该样本点的输出值。具体的算法流程如图2所示：

图 2 LLE算法步骤

 

Laplacian Eigenmaps 拉普拉斯特征映射

继续写一点经典的降维算法，前面介绍了PCA,LDA，LLE，这里讲一讲Laplacian Eigenmaps。其实不是说每一个算法都比前面的好，而是每一个算法都是从不同角度去看问题，因此解决问题的思路是不一样的。这些降维算法的思想都很简单，却在有些方面很有效。这些方法事实上是后面一些新的算法的思路来源。

Laplacian Eigenmaps[1] 看问题的角度和LLE有些相似，也是用局部的角度去构建数据之间的关系。

它的直观思想是希望相互间有关系的点（在图中相连的点）在降维后的空间中尽可能的靠近。Laplacian Eigenmaps可以反映出数据内在的流形结构。

使用时算法具体步骤为：

步骤1：构建图

使用某一种方法来将所有的点构建成一个图，例如使用KNN算法，将每个点最近的K个点连上边。K是一个预先设定的值。

步骤2：确定权重

确定点与点之间的权重大小，例如选用热核函数来确定，如果点i和点j相连，那么它们关系的权重设定为：

使用最小的m个非零特征值对应的特征向量作为降维后的结果输出。

前面提到过，Laplacian Eigenmap具有区分数据点的特性，可以从下面的例子看出：

图1 Laplacian Eigenmap实验结果

见图1所示，左边的图表示有两类数据点（数据是图片），中间图表示采用Laplacian Eigenmap降维后每个数据点在二维空间中的位置，右边的图表示采用PCA并取前两个主要方向投影后的结果，可以清楚地看到，在此分类问题上，Laplacian Eigenmap的结果明显优于PCA。

 

图2 roll数据的降维

图2说明的是，高维数据（图中3D）也有可能是具有低维的内在属性的（图中roll实际上是2D的），但是这个低维不是原来坐标表示，例如如果要保持局部关系，蓝色和下面黄色是完全不相关的，但是如果只用任何2D或者3D的距离来描述都是不准确的。

下面三个图是Laplacian Eigenmap在不同参数下的展开结果（降维到2D），可以看到，似乎是要把整个带子拉平了。于是蓝色和黄色差的比较远。

 

ISOMAP是‘流形学习’中的一个经典算法，流形学习贡献了很多降维算法，其中一些与很多机器学习算法也有结合，但上学的时候还看了蛮多的机器学习的书，从来没听说过流形学习的概念，还是在最新的周志华版的《机器学习》里才看到,很有意思，记录分享一下。

流形学习

流形学习应该算是个大课题了，它的基本思想就是在高维空间中发现低维结构。

比如这个图：

 
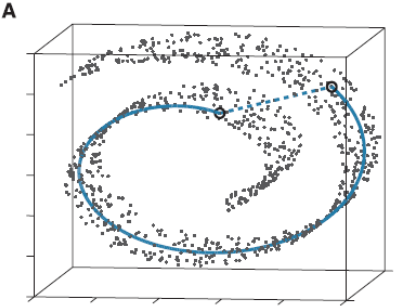
这些点都处于一个三维空间里，但我们人一看就知道它像一块卷起来的布，图中圈出来的两个点更合理的距离是A中蓝色实线标注的距离，而不是两个点之间的欧式距离（A中蓝色虚线）。

此时如果你要用PCA降维的话，它根本无法发现这样卷曲的结构（因为PCA是典型的线性降维，而图示的结构显然是非线性的），最后的降维结果就会一团乱麻，没法很好的反映点之间的关系。而流形学习在这样的场景就会有很好的效果。

我对流形学习本身也不太熟悉，还是直接说算法吧。

ISOMAP

在降维算法中，一种方式是提供点的坐标进行降维，如PCA；另一种方式是提供点之间的距离矩阵，ISOMAP中用到的MDS(Multidimensional Scaling)就是这样。 
在计算距离的时候，最简单的方式自然是计算坐标之间的欧氏距离，但ISOMAP对此进行了改进，就像上面图示一样：

1.通过kNN(k-Nearest Neighbor)找到点的k个最近邻，将它们连接起来构造一张图。 
2.通过计算同中各点之间的最短路径，作为点之间的距离dijdij放入距离矩阵DD 
3.将DD传给经典的MDS算法，得到降维后的结果。

ISOMAP本身的核心就在构造点之间的距离，初看时不由得为其拍案叫绝，类似的思想在很多降维算法中都能看到，比如能将超高维数据进行降维可视化的t-SNE。 
ISOMAP效果，可以看到选取的最短路径比较好地还原了期望的蓝色实线，用这个数据进行降维会使流形得以保持： 

ISOMAP算法步骤可谓清晰明了，所以本文主要着重讲它中间用到的MDS算法，也是很有意思的。

经典MDS（Multidimensional Scaling）

如上文所述，MDS接收的输入是一个距离矩阵DD,我们把一些点画在坐标系里： 
 
如果只告诉一个人这些点之间的距离（假设是欧氏距离），他会丢失那些信息呢？ 
a.我们对点做平移，点之间的距离是不变的。 
b.我们对点做旋转、翻转，点之间的距离是不变的。

所以思路是：从D->B->X 
此时我们要对X加一些限制，前面说过我们平移所有点是不会对距离矩阵造成影响的，所以我们就把数据的中心点平移到原点，对X做如下限制（去中心化）： 

 

如果选择p=q的话，此时得到的X∗X∗就是原数据去中心化并做了某种正交变换后的值了。

MDS的例子

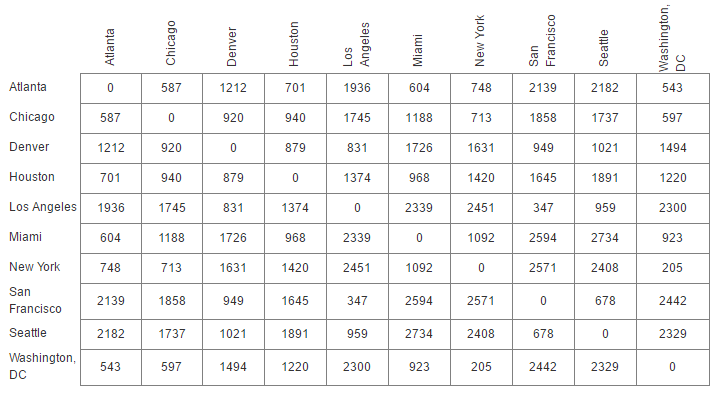
举个例子：拿美国一些大城市之间的距离作为矩阵传进去，简单写一写代码： 

import numpy as np
import matplotlib.pyplot as pltdef mds(D,q):D = np.asarray(D)DSquare = D**2totalMean = np.mean(DSquare)columnMean = np.mean(DSquare, axis = 0)rowMean = np.mean(DSquare, axis = 1)B = np.zeros(DSquare.shape)for i in range(B.shape[0]):for j in range(B.shape[1]):B[i][j] = -0.5*(DSquare[i][j] - rowMean[i] - columnMean[j]+totalMean)eigVal,eigVec = np.linalg.eig(B)X = np.dot(eigVec[:,:q],np.sqrt(np.diag(eigVal[:q])))return XD = [[0,587,1212,701,1936,604,748,2139,2182,543],
[587,0,920,940,1745,1188,713,1858,1737,597],
[1212,920,0,879,831,1726,1631,949,1021,1494],
[701,940,879,0,1374,968,1420,1645,1891,1220],
[1936,1745,831,1374,0,2339,2451,347,959,2300],
[604,1188,1726,968,2339,0,1092,2594,2734,923],
[748,713,1631,1420,2451,1092,0,2571,2408,205],
[2139,1858,949,1645,347,2594,2571,0,678,2442],
[2182,1737,1021,1891,959,2734,2408,678,0,2329],
[543,597,1494,1220,2300,923,205,2442,2329,0]]label = ['Atlanta','Chicago','Denver','Houston','Los Angeles','Miami','New York','San Francisco','Seattle','Washington, DC']
X = mds(D,2)
plt.plot(X[:,0],X[:,1],'o')
for i in range(X.shape[0]):plt.text(X[i,0]+25,X[i,1]-15,label[i])
plt.show()

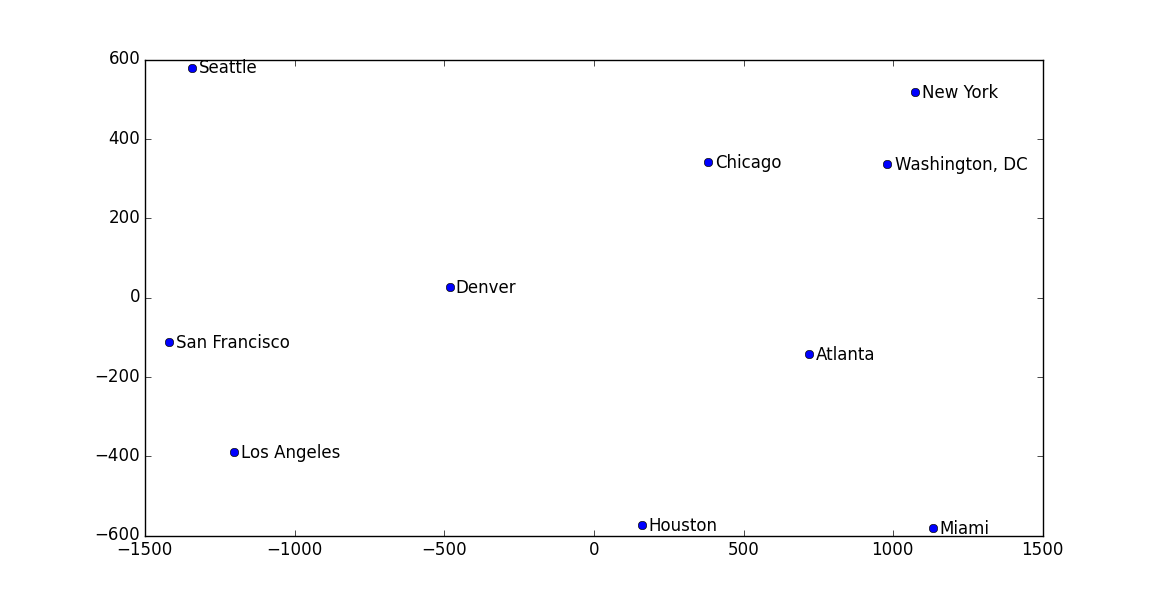
最后画出来的图中，各个城市的位置和真实世界中的相对位置都差不多: 

注意，这个例子中其实也有‘流形’在里面，因为我们的地球其实是一个三维，而城市间距离刻画的是在球面上的距离，所以最后如果你去看求出来的特征值，并不像前面说的那样只有q个非0的值。

 

SNE、TSNE

TSNE是由SNE衍生出的一种算法，SNE最早出现在2002年，它改变了MDS和ISOMAP中基于距离不变的思想，将高维映射到低维的同时，尽量保证相互之间的分布概率不变，SNE将高维和低维中的样本分布都看作高斯分布，而Tsne将低维中的坐标当做T分布，这样做的好处是为了让距离大的簇之间距离拉大，从而解决了拥挤问题。从SNE到TSNE之间，还有一个对称SNE，其对SNE有部分改进作用。

1、SNE

高维数据用X表示，Xi表示第i个样本，低维数据用Y表示，则高维中的分布概率矩阵P定义如下：

P(i,j)表示第i个样本分布在样本j周围的概率。delta是依据最大熵原理来决定，entropy=sum(pi*log(pi))，以每个样本点作为中心的delta都需要使得最后分布的熵较小，通常以log(k)为上限，k为你所决定的邻域点的个数。

低维中的分布概率矩阵计算如下：

这里我们把低维中的分布看作是均衡的，每个delta都是0.5，由此可以基本判断最后降维之后生成的分布也是一个相对均匀的分布。

随机给定一个初始化的Y，进行优化，使得Y的分布矩阵逼近X的分布矩阵。我们给定目的函数，用KL散度来定义两个不同分布之间的差距：

则可以计算梯度为：

每次梯度下降的步长可设定固定或者自适应、随机等，也可以加上一个动量的梯度，初始值一般设为1e-4的随机正态分布。

 

2、对称SNE

顾名思义，就是让高维和低维中的概率分布矩阵是对称的，能方便运算，但是对拥挤问题无改进。

同样采用KL散度作为两个分布之间的差异标准，只是梯度有一些改变：

3、TSNE

TSNE对高维中的分布采用对称SNE中的做法，低维中的分布则采用更一般的T分布，也是对称的，我们可以发现sum(P)=sum(Q)=1。

TSNE算法流程如下：

自TSNE极大改良了SNE，但它们都有一个非常通用的毛病，耗时耗力。样本较多时，构建网络及其困难，梯度下降太慢，TSNE的程序及可视化见下一篇，TSNE的改良Largevis见下下篇。

 

reference

1. 一个MDS的例子，用于数据可视化，例子的数据来源于这里。http://www.benfrederickson.com/multidimensional-scaling/
2. 周志华《机器学习》

这篇关于【机器学习】降维算法 PCA、LDA、LLE、Laplacian EigenmapsI、SOMAP 、 MDS、SNE、TSNE的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---