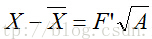mds专题

各种数据降维方法ICA、 ISOMAP、 LDA、LE、 LLE、MDS、 PCA、 KPCA、SPCA、SVD、 JADE

各种数据降维方法ICA、 ISOMAP、 LDA、LE、 LLE、MDS、 PCA、 KPCA、SPCA、SVD、 JADE

独立分量分析 ICA 等度量映射 ISOMAP 线性判别分析 LDA (拉普拉斯)数据降维方法 LE 局部线性嵌入 LLE 多维尺度变换MDS 主成分分析 PCA 核主成分分析 KPCA 稀疏主成分分析SPCA 奇异值分解SVD 特征矩阵的联合近似对角化 JADE 各种数据降维方法(matlab代码)代码获取戳此处代码获取戳此处 降维目的：克服维数灾难，获取本质特征，节省存储空
阅读更多...
基于MDS的波士顿房价数据集降维

基于MDS的波士顿房价数据集降维

文章目录 1. 作者介绍2. 多维尺度分析（Multi-Dimensional Scaling, MDS）介绍2.1 MDS介绍2.2 MDS的类别2.2.1度量MDS2.2.2非度量MDS 2.3 目标函数2.4 MDS降维计算步骤2.4.1计算流程2.4.2 算法示例 3．实验过程3.1数据集介绍3.2算法思路3.3算法评价3.4与其他降维算法相比3.4.1主成分分析3.4.2 t-S
阅读更多...
数据特征降维 | 多维缩放（MDS）附Python代码

数据特征降维 | 多维缩放（MDS）附Python代码

多维缩放（Multidimensional Scaling，MDS）是一种经典的降维和可视化技术，用于将高维数据映射到低维空间中，以便更好地展示数据的相似性和差异性。 MDS的基本思想是通过测量样本之间的距离或相似性，将其映射到低维空间中，使得在低维空间中的距离能够保持或近似原始高维空间中的距离。通过这种方式，MDS可以展示数据样本之间的关系和结构，并提供直观的可视化结果。 以下是MDS的基本
阅读更多...
ceph mds 文件系统的挂载方式

ceph mds 文件系统的挂载方式

概述 近期测试发现，部分版本和服务器使用ceph mds内核态挂载时，性能较差，可能和存储和系统版本有关，用户态性能反而更稳定，这里补充两种挂载方式。 内核态 开启ceph认证，使用admin挂载，monip为任意monip即可，secret指定auth中的admin keyring，/mnt/fs_kernel为挂载目录 mount -t ceph monip:6789:/ /mnt/f
阅读更多...
多尺度变换（Multidimensional Scaling ，MDS）详解

多尺度变换（Multidimensional Scaling ，MDS）详解

一、基本思想         MDS（Multidimensional Scaling ，MDS多维尺度变换）是一种经典的降维算法，其基本思想是通过保持数据点之间的距离关系，将高维数据映射到低维空间中。 具体来说，MDS算法的基本步骤如下： 1、构建距离矩阵：首先，我们需要计算原始空间中数据点之间的距离。常用的距离度量方法包括欧几里得距离、Minkowski距离等。通过计算每对数据点之间
阅读更多...
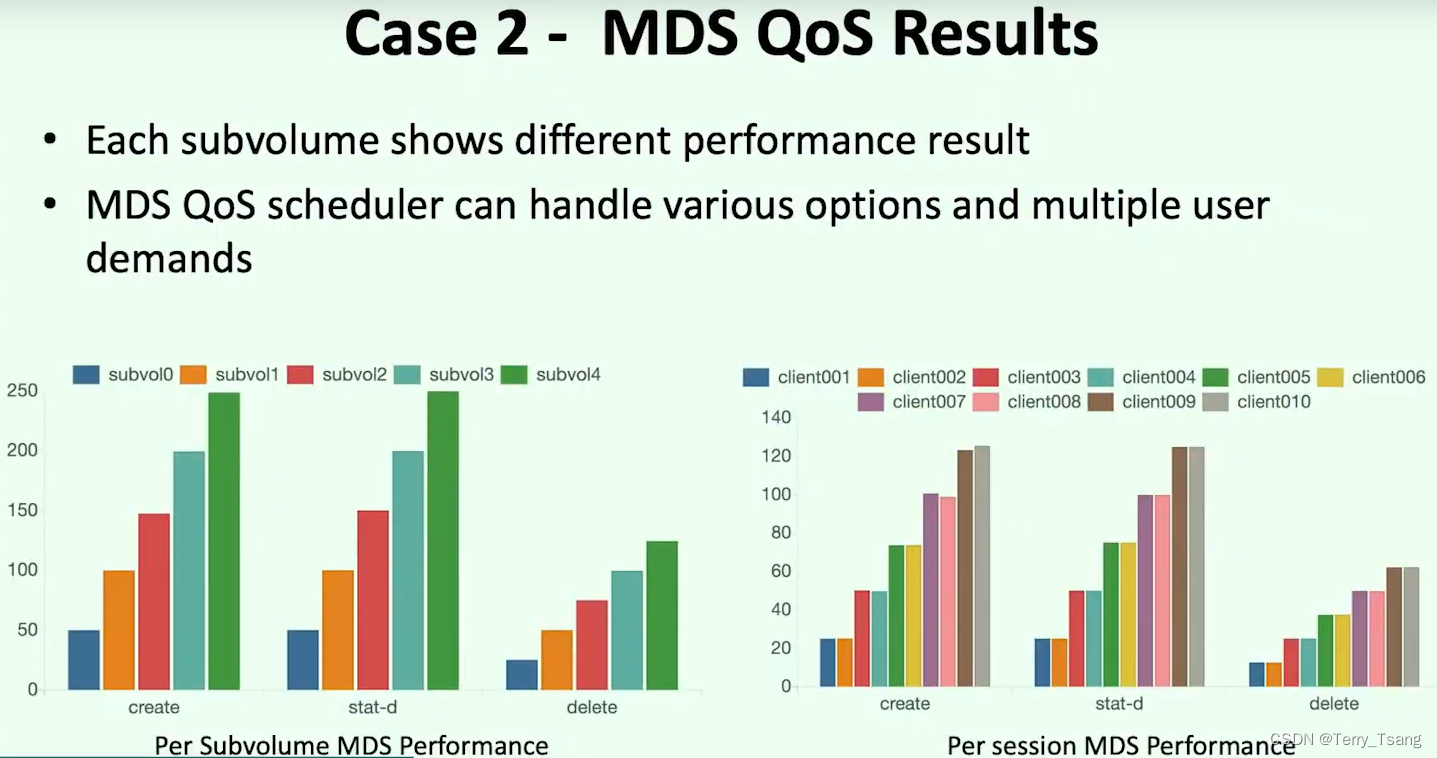
cephfs mds mclock qos scheduler

cephfs mds mclock qos scheduler

目标 了解 cephfs qos 方法 用于限制 cpehfs client QOS 等 capture 1 使用了 mclock 非 dmclock 2 qos 在 MDS 中进行限制 1 通过subvolume 进行设定 issue 关注 https://github.com/ceph/ceph/pull/52147
阅读更多...
【聚类】|多维尺度分析 MDS

【聚类】|多维尺度分析 MDS

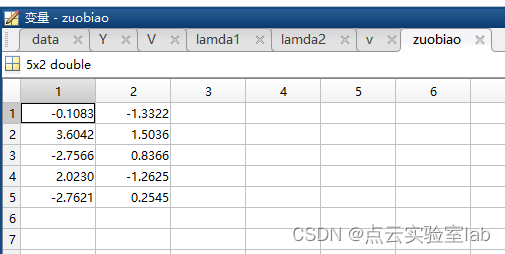
ref https://blog.csdn.net/Dark_Scope/article/details/53229427 1 目的 已知很多样本点之间的相互距离（以欧式距离为例），但是不知道每个样本点的具体坐标，MDS分析就是要求解出每个样本点的原始坐标，然后保证这些样本点的原始坐标尽量符合这个距离矩阵关系。 MDS利用的是成对样本间相似性，目的是利用这个信息去构建合适的低维空间，是的样本
阅读更多...
【EI会议征稿】第四届机械设计与仿真国际学术会议（MDS 2024)

【EI会议征稿】第四届机械设计与仿真国际学术会议（MDS 2024)

【高录用快检索】第四届机械设计与仿真国际学术会议（MDS 2024)  2024 4th International Conference on Mechanical Design and Simulation  2024年第四届机械设计与仿真国际学术会议（MDS 2024) 将于2024年03月01-03日在中国西安召开。MDS 2024将围绕“机械设计”、“机械工程”与“建模与仿真技术”等
阅读更多...
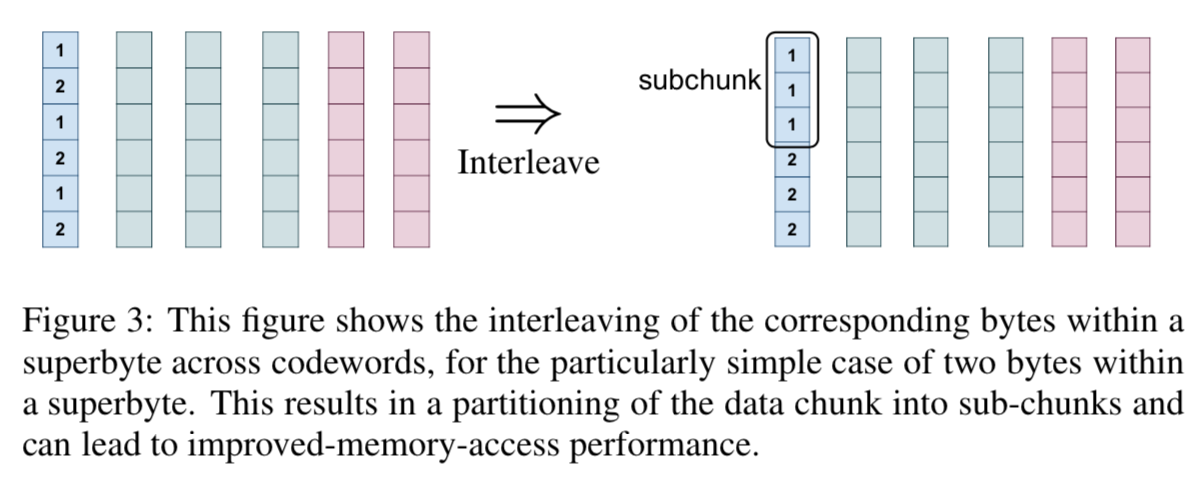
Note: Clay Codes: Moulding MDS Codes to Yield an MSR Code

Note: Clay Codes: Moulding MDS Codes to Yield an MSR Code

Background Erasure Code 纠删码：与纠错码、检错码类似，均为线性分组码，通过编码可以在有限损失的前提下恢复丢失的数据。 假设每个磁盘存储w比特数据，设d0，⋯，dk−1d0，⋯，dk−1 是存储在k个数据磁盘上的数据，c0，⋯，cm−1c0，⋯，cm−1 是存储在m个编码盘上的编码。编码定义为数据的线性组合： c0=a(0,0)d0+⋯+a(0,k−1)dk−1c0
阅读更多...
Multidimensional Scaling（MDS多维缩放）算法及其应用

Multidimensional Scaling（MDS多维缩放）算法及其应用

在这篇博客中，我将与大家分享在流形分析领域的一个非常重要的方法，即多维缩放MDS。整体来说，该方法提供了一种将内蕴距离映射到显性欧氏空间的计算，为非刚性形状分析提供了一种解决方案。当初就是因为读了Bronstein的相关工作【1】，才下定决心在人脸数据分析中使用内蕴度量来建立特征分析方法，可以说MDS对我的学术之路起到了很大的影响作用。 1. 前言 在非刚性形状匹配中，我们希望找到两个曲面
阅读更多...
【机器学习】降维算法 PCA、LDA、LLE、Laplacian EigenmapsI、SOMAP 、 MDS、SNE、TSNE

【机器学习】降维算法 PCA、LDA、LLE、Laplacian EigenmapsI、SOMAP 、 MDS、SNE、TSNE

机器学习领域中所谓的降维就是指采用某种映射方法，将原高维空间中的数据点映射到低维度的空间中。降维的本质是学习一个映射函数 f : x->y，其中x是原始数据点的表达，目前最多使用向量表达形式。 y是数据点映射后的低维向量表达，通常y的维度小于x的维度（当然提高维度也是可以的）。f可能是显式的或隐式的、线性的或非线性的。 目前大部分降维算法处理向量表达的数据，也有一些降维算法处理高阶张量表达的数据
阅读更多...
【文章导读】什么是旁道攻击？Meltdown Redux英特尔漏洞（MDS攻击）；KAISER：从用户空间隐藏内核（KAISER）；Meltdown/Spectre分析

【文章导读】什么是旁道攻击？Meltdown Redux英特尔漏洞（MDS攻击）；KAISER：从用户空间隐藏内核（KAISER）；Meltdown/Spectre分析

Table of Contents 黑客词典：什么是旁道攻击？ Meltdown Redux：Intel缺陷使黑客窃取了数百万台PC的秘密 三重熔毁：有多少研究人员同时发现了20年的芯片缺陷 KAISER：从用户空间隐藏内核 迟到的Meltdown/Spectre分析   黑客词典：什么是旁道攻击？ https://www.wired.com/story/what-is-s
阅读更多...
【数据降维-第4篇】多维尺度变换（MDS）快速理解，及MATLAB实现

【数据降维-第4篇】多维尺度变换（MDS）快速理解，及MATLAB实现

这篇是继PCA和KPCA、t-SNE三种降维方法后的第4篇。 在大数据时代，我们不断面临高维度数据的挑战。为了更好地理解这些数据，MDS算法应运而生。本文将详细介绍MDS算法的原理、步骤及其应用场景，帮助你深入了解这个强大的降维工具。 一、关于MDS算法 多维尺度变换（Multidimensional Scaling，简称MDS）算法是一种数据降维和可视化方法，最早起源于心理学领域，它能够将
阅读更多...
现代数据堆栈MDS有什么现代之处

现代数据堆栈MDS有什么现代之处

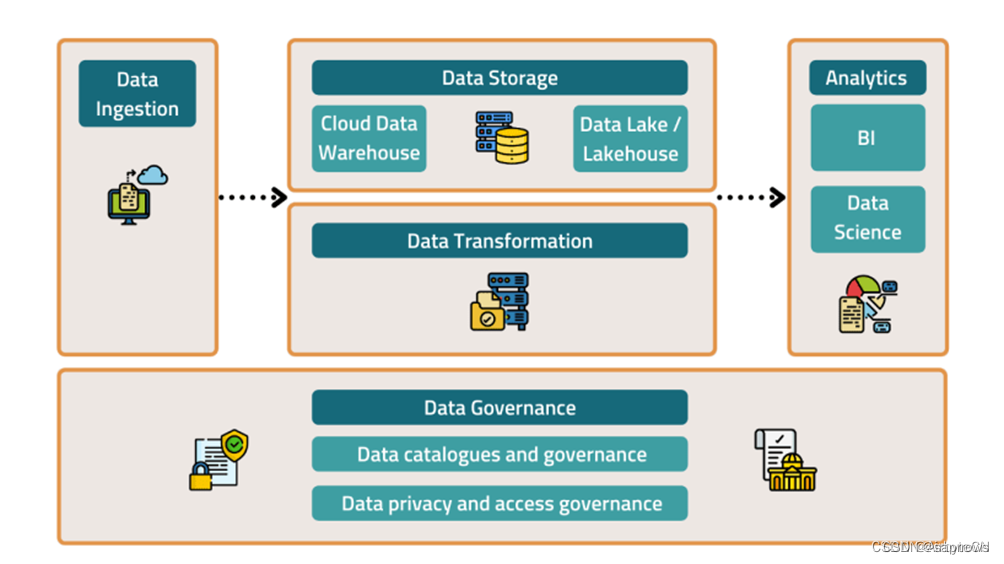
Dazdata MDS 现代数据堆栈（MDS）已经普及了几年，但直到最近才在其定义上趋同。在我们深入探讨MDS的哲学和技术指标之前，让我们先谈谈传统数据堆栈的失败。 为什么MDS越来越受欢迎？ 原因很简单，传统数据堆栈 （TDS） 无法满足任何现代组织的数据需求。为了保持竞争优势，组织需要能够在正确的时间采取行动的数据，并且足够灵活地适应变化。TDS通常是指逻辑耦合且复杂的本地Hadoop（
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2