本文主要是介绍Note: Clay Codes: Moulding MDS Codes to Yield an MSR Code,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Background
Erasure Code
纠删码:与纠错码、检错码类似,均为线性分组码,通过编码可以在有限损失的前提下恢复丢失的数据。 

假设每个磁盘存储w比特数据,设d0,⋯,dk−1d0,⋯,dk−1 是存储在k个数据磁盘上的数据,c0,⋯,cm−1c0,⋯,cm−1 是存储在m个编码盘上的编码。编码定义为数据的线性组合:
c0=a(0,0)d0+⋯+a(0,k−1)dk−1c0=a(0,0)d0+⋯+a(0,k−1)dk−1
c1=a(1,0)d0+⋯+a(1,k−1)dk−1c1=a(1,0)d0+⋯+a(1,k−1)dk−1
⋯⋯⋯⋯
cm−1=a(m−1,0)d0+⋯+a(m−1,k−1)dk−1cm−1=a(m−1,0)d0+⋯+a(m−1,k−1)dk−1
编码只需要乘法和加法(w=1w=1 时加法指模2加/异或、乘法指二进制与运算),解码需要用高斯消除或矩阵求逆求的方法解一组线性方程。
译码准则:最小差错概率译码、最大似然译码
以上计算建立在GF(2w)GF(2w) 上,这里的w值一般选取2的幂,较为流行的值有w=1w=1 (计算简单)w=8w=8 (一个字节)w值越大,纠删码越丰富,但随w值增大,在伽罗瓦域上的计算复杂度不断提高。
GF(2w)GF(2w) 扩展域上的计算
加法、减法
假设A(x),B(x)∈GF(2w)A(x),B(x)∈GF(2w) ,求和结果为C(x)C(x) 。
C(x)=A(x)+B(x)=∑i=0w−1cixi,ci≡ai+bimod2C(x)=A(x)+B(x)=∑i=0w−1cixi,ci≡ai+bimod2
乘法
假设A(x),B(x)∈GF(2w)A(x),B(x)∈GF(2w) ,且
P(x)=∑i=0w−1pixi,pi∈GF(2)P(x)=∑i=0w−1pixi,pi∈GF(2)
是一个不可约多项式。两个元素的乘法运算定义为:
C(x)=A(x)⋅B(x)modP(x)C(x)=A(x)⋅B(x)modP(x)
求逆
在乘法中定义的P(x)P(x) 基础上,任一非零元A∈GF(2w)A∈GF(2w) 的逆元定义为:
A−1(x)⋅A(x)≡1modP(x)A−1(x)⋅A(x)≡1modP(x)
Scalar Codes
 

让每个数据块由L个字节组成。在标量码的情况下,从k个数据块中的每一个中挑选一个字节,并且以m个不同的方式将k个字节以线性方式组合,以获得m个奇偶校验字节。所得到的n=k+mn=k+m 个字节的集合称为码字。对数据块中的所有L字节并行重复该操作以获得L个码字。 这个操作也会产生m个奇偶校验块,每个奇偶校验块由L个字节组成。
Vector Codes
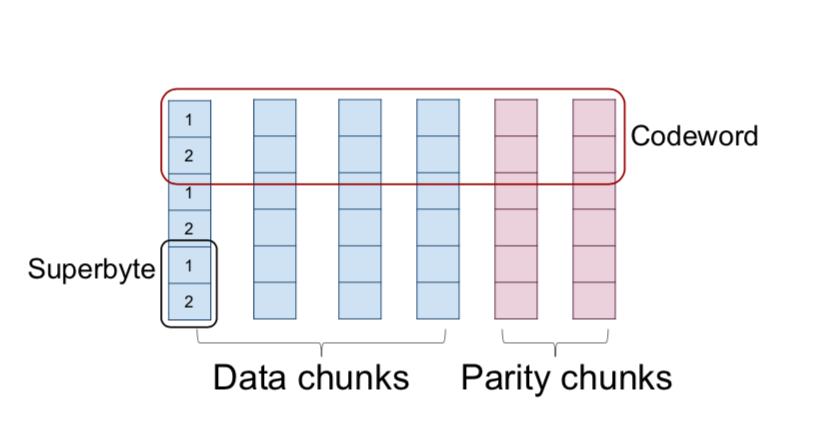 

选取α⩾1α⩾1 个字节组(形成superbyte). 在编码过程中,选取k个数据块中的每个数据块的superbyte,然后以m种不同的方式线性组合k个超级字节,以获得m个奇偶校验超级字节。 所得到的n=k+mn=k+m 个superbyte称为(矢量)码字。
MDS Codes
一个(n,n-r,r+1)(n,n-r,r+1) 码称为最大距离可分(Maximum Distance Separable, MDS)码。一个MDS码是冗余度为r,最小距离等于r+1的线性码。(实现最佳容错能力)
Reed-Solomon Codes(RS码)
RS码是当且仅当n⩽2wn⩽2w 时存在的MDS码。例如,存储系统包含256个或更少的磁盘,可以在GF(28)GF(28) 中定义一种计算。有多种方式来定义a(i,j)a(i,j) 系数。
最简单是“Cauchy”结构:在GF(2w)GF(2w) 中选择n个不同的数字,并将它们分成两组X和Y,使得X具有m个元素,Y具有k个元素。计算纠删码系数:
a(i,j)=1xi⊕yja(i,j)=1xi⊕yj
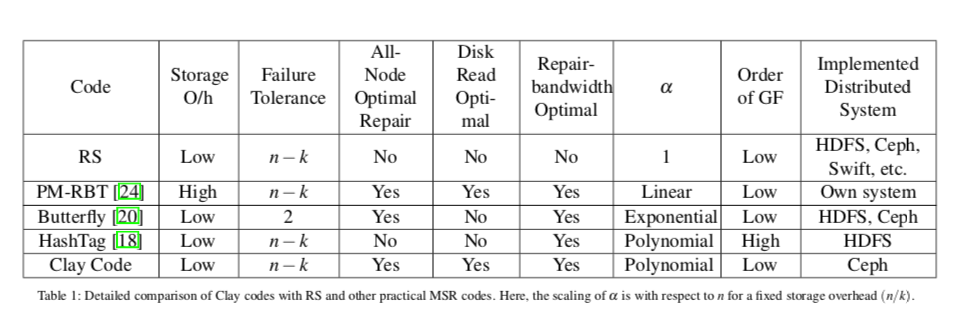
MSR Codes
矢量性质的MDS码(修复时占用带宽最少)

Node Repair
节点修复分布式存储系统中对节点修复的需求可能是由于特定的硬件组件出现故障,由节点修复请求引起的流量吞噬可用于服务用户数据请求的带宽。节点修复所花费的时间也直接影响系统可用性。
Sub-chunking through Interleaving
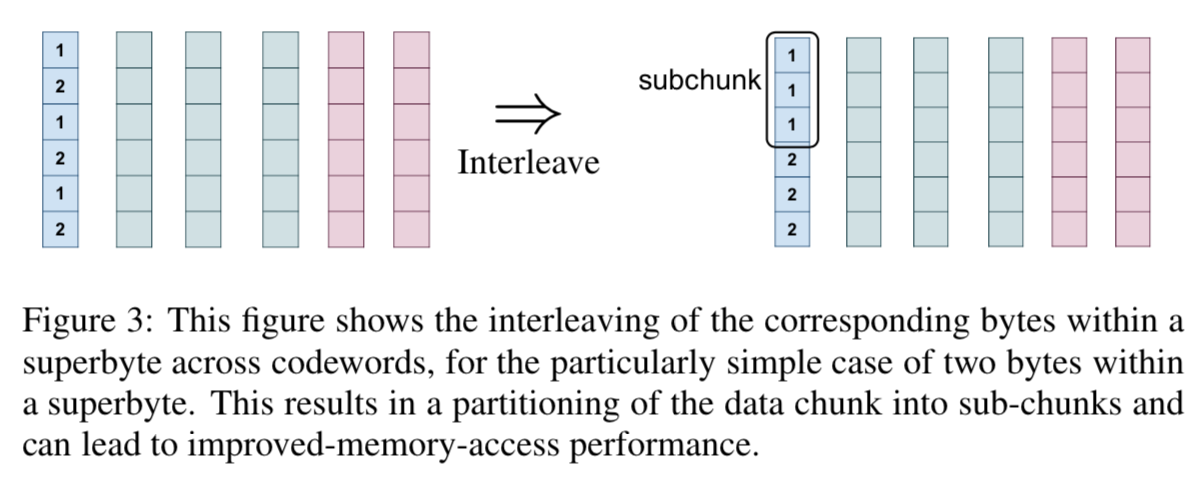 

当分包级别αα 很大时,考虑到涉及多个码字的操作是并行执行的,从存储器易于访问的角度考虑,插入字节是有利的, 如图3所示,跨越不同码字的相应字节被连续存储。当块内的超字节的数目N很大时,例如当L = 8KB并且αα = 2时,连续访问N = 4K 字节是可能的。 通过交织,每个数据块被分割成一个子集,称之为子组块。 因此,节点内的每个子块保存存储在该节点中的N个码字中的每一个的一个字节。
这篇关于Note: Clay Codes: Moulding MDS Codes to Yield an MSR Code的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







