pca专题
《机器学习》PCA数据降维 推导、参数讲解、代码演示及分析
目录 一、主成分分析 1、什么是主成分分析? 2、什么是降维? 3、如何进行主成分分析 1)数据标准化 2)计算协方差矩阵 3)计算特征值和特征向量 4)选择主成分 5)构建投影矩阵 6)数据降维 4、为什么要进行主成分分析 1)数据可视化 2)
《机器学习》—— PCA降维
文章目录 一、PCA降维简单介绍二、python中实现PCA降维函数的介绍三、代码实现四、PCA降维的优缺点 一、PCA降维简单介绍 PCA(主成分分析,Principal Component Analysis)是一种常用的数据降维技术。它通过线性变换将原始数据转换到新的坐标系统中,使得任何投影的第一大方差在第一个坐标(称为第一主成分)上,第二大方差在第二个坐标(第二主成分)上,
【C++】PCA原理
PCA原理 看到了Angry Master博客的文章,写的很浅显易懂,就转来了:http://pan.baidu.com/share/link?shareid=84575&uk=3106100059
PCA降维奇异值分解SVD
PCA降维 涉及高维数据的问题容易陷入维数灾难,随着数据集维数的增加,算法学习所需的样本数量呈指数级增加,且需要更多的内存和处理能力,消耗资源。主成分分析也称为K-L变换,常用于高位数据预处理和可视化。PCA可以把可能具有相关性的高维变量合成线性无关的低维变量,称为主成分。原理就是PCA将高维具有相关性的数据进行线性变换映射到一个低维子空间,尽可能多的保留更多变量(代表原特征),降维成一个线性无
数据降维技术——PCA(主成分分析)
为什么要对数据进行降维? 在机器学习或者数据挖掘中,我们往往会get到大量的数据源,这些数据源往往有很多维度来表示它的属性,但是我们在实际处理中只需要其中的几个主要的属性,而其他的属性或被当成噪声处理掉。比如,13*11的源数据经过将为后变成了13*4的优化数据,那么,中间就减去了7个不必要的属性,选取了4个主要属性成分,简化了计算。 常用的数据降维方法有:主成分分析
运用PCA(主成分分析法)进行人脸识别的MATLAB 代码实现
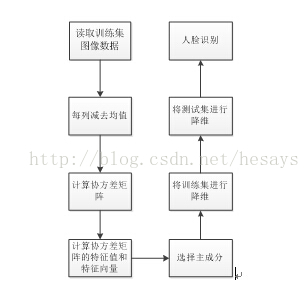
PCA(主成分分析算法)出现的比较早。 PCA算法依赖于一个基本假设:一类图像具有某些相似的特征(如人脸),在整个图像空间中呈现出聚类性,因而形成一个子空间,即所谓特征子空间,PCA变换是最佳正交变换,利用变换基的线性组合可以描述、表达和逼近这一类图像,因此可以进行图像识别,PCA包含训练和识别两个阶段。 训练阶段: 1)计算平均脸 2)计算差值脸 3)构建协方差矩阵 4)计算矩阵的特
各种数据降维方法ICA、 ISOMAP、 LDA、LE、 LLE、MDS、 PCA、 KPCA、SPCA、SVD、 JADE
独立分量分析 ICA 等度量映射 ISOMAP 线性判别分析 LDA (拉普拉斯)数据降维方法 LE 局部线性嵌入 LLE 多维尺度变换MDS 主成分分析 PCA 核主成分分析 KPCA 稀疏主成分分析SPCA 奇异值分解SVD 特征矩阵的联合近似对角化 JADE 各种数据降维方法(matlab代码)代码获取戳此处代码获取戳此处 降维目的:克服维数灾难,获取本质特征,节省存储空
【机器学习】独立成分分析的基本概念、应用领域、具体实例(含python代码)以及ICA和PCA的联系和区别
引言 独立成分分析(Independent Component Analysis,简称ICA)是一种统计方法,用于从多个观察到的混合信号中提取出原始的独立信号源 文章目录 引言一、独立成分分析1.1 定义1.2 独立成分分析的基本原理1.3 独立成分分析的步骤1.3.1 观察数据收集1.3.2 数据预处理1.3.3 ICA模型建立1.3.4 ICA算法实现1.3.5 源信号提取1.
漫谈Deep PCA与PCANet
又到了无聊的写博客的时间了,由于电脑在跑程序,目前无事可做,我觉得把昨天我看的一些论文方面的知识拿出来和大家分享一下。 美其名曰我是在研究”深度学习“,不过由于本人是穷屌丝一个,买不起GPU(当然明年我准备入手一块显卡来玩玩),因此这半年我找了个深度学习中的一个”便宜“的方向——PCANet。 首先给出PCANet的原始文献《PCANet:A Simple Deep Lear
吴恩达机器学习课后作业-07kmeans and pca
k-均值与PCA k-均值图片颜色聚类 PCA(主成分分析)对x去均值化图像降维 k-均值 K-均值是最普及的聚类算法,算法接受一个未标记的数据集,然后将数据聚类成不同的组。 K-均值是一个迭代算法,假设我们想要将数据聚类成n个组,其方法为: 首先选择K个随机的点,称为聚类中心(cluster centroids); 对于数据集中的每一个数据,按照距离K个中心点的距离,将其与距
机器学习 | 基于wine数据集的KMeans聚类和PCA降维案例
KMeans聚类:K均值聚类是一种无监督的学习算法,它试图根据数据的相似性对数据进行聚类。无监督学习意味着不需要预测结果,算法只是试图在数据中找到模式。在k均值聚类中,我们指定希望将数据分组到的聚类数。该算法将每个观察随机分配到一个集合,并找到每个集合的质心。然后,该算法通过两个步骤进行迭代:将数据点重新分配到质心最近的聚类。计算每个簇的新质心。重复这两个步骤,直到集群内的变化不能进一步减少。聚类
Python实现PCA算法
博客目录 引言 什么是PCA(主成分分析)?PCA的应用场景为什么选择PCA? PCA的数学原理 数据标准化协方差矩阵的计算特征值与特征向量主成分的选择数据的降维 PCA的实现步骤 数据预处理计算协方差矩阵计算特征值与特征向量选择主成分转换原始数据 Python实现PCA 使用NumPy手动实现PCA使用Scikit-learn实现PCA代码示例与解释 PCA应用实例:图像降维 场景描
数学建模学习(115):主成分分析(PCA)与Python实践
文章目录 一.主成分分析简介1.1 数学背景与维度诅咒1.2 PCA的定义与应用 二.协方差矩阵——特征值和特征向量三.如何为数据集选择主成分数量四.特征提取方法五.LDA——与PCA的区别六.PCA的应用七.PCA在异常检测中的应用八.总结 一.主成分分析简介 1.1 数学背景与维度诅咒 主成成分分析(PCA)是一种广泛使用的算法,用于从高维数据中提取主要特征,以便更有效地
机器学习实战 --- 利用PCA简化数据
降维技术 — 场景: 我们正在通过电视观看体育比赛,在电视的显示器上有一个球。 显示器大概包含100W个像素点,而球则可能是由较少的像素点组成,例如说一千个像素点。 人们在实时的将显示器上的百万像素转化成为一个三维图形,该图像就给出运动场上球的位置。 在这个过程中,人们已经将百万像素点的数据,降维到三维。这个过程就称为降维(dimensionality reduction)
深入理解主成分分析 (PCA) 及其广泛应用
深入理解主成分分析 (PCA) 及其广泛应用 文章目录 深入理解主成分分析 (PCA) 及其广泛应用引言PCA 的核心概念与目标PCA 的几何解释与步骤具体数值计算例子如果 PCA 中维度和执行 PCA 之前的维度保持一致,会发生什么?Python 实现 PCA实例解析:二维数据的 PCA 应用实际应用场景与总结 引言 主成分分析(Principal Compon
如何确定PCA降维的维度
主要是对西瓜书里面的一个思路的实现,并不涉及PCA原理和公式推导,用一句话总结PCA,在 R d R^{d} Rd中的m个点经过矩阵变换(压缩)映射到 R d ′ R^{d'} Rd′空间中,并且保证 d ′ < d d'<d d′<d,其中 d ′ d' d′是新维度。 用矩阵表示: Z d ′ ∗ m = W d ′ ∗ d T ∗ X d ∗ m Z_{d'*m}=W^{T}_{d'*d}
主成分分析PCA详解(二)
我不生产自己不熟悉的内容,我只是陌生内容的搬运工!向原作致敬! 转载自:http://blog.csdn.net/jzwong/article/details/45699097 作者:jzwong 一、简介 PCA(Principal Components Analysis)即主成分分析,是图像处理中经常用到的降维方法,大家知道,我们在处理有关数字图像处理方面的问题时,比如经
主成分分析PCA详解(一)
对理解PCA非常好的一篇文章,留着以防以后忘记 原文来自:博客园(华夏35度)http://www.cnblogs.com/zhangchaoyang 作者:Orisun 降维的必要性 1.多重共线性--预测变量之间相互关联。多重共线性会导致解空间的不稳定,从而可能导致结果的不连贯。 2.高维空间本身具有稀疏性。一维正态分布有68%的值落于正负标准差之间,而在十维空间上只有0.02%。
【Python机器学习实战】 | 基于PCA主成分分析技术读入空气质量监测数据进行数据预处理并计算空气质量综合评测结果
🎩 欢迎来到技术探索的奇幻世界👨💻 📜 个人主页:@一伦明悦-CSDN博客 ✍🏻 作者简介: C++软件开发、Python机器学习爱好者 🗣️ 互动与支持:💬评论 👍🏻点赞 📂收藏 👀关注+ 如果文章有所帮助,欢迎留下您宝贵的评论, 点赞加收藏支持我,点击关注,一起进步! 引言 主成分分析(Principal Component
PCA使用SVD解决
http://www.cnblogs.com/LeftNotEasy/archive/2011/01/19/svd-and-applications.html 主成分分析在上一节里面也讲了一些,这里主要谈谈如何用SVD去解PCA的问题。PCA的问题其实是一个基的变换,使得变换后的数据有着最大的方差。方差的大小描述的是一个变量的信息量,我们在讲一个东西的稳定性的时候,往往说要减小方差,如果一个模
文本挖掘之降维之特征抽取之主成分分析(PCA)
PCA(主成分分析) 作用: 1、减少变量的的个数 2、降低变量之间的相关性,从而降低多重共线性。 3、新合成的变量更好的解释多个变量组合之后的意义 PCA的原理: 样本X和样本Y的协方差(Covariance): 协方差为正时说明X和Y是正相关关系,协方差为负时X和Y是负相关关系,协方差为0时X和Y相互独立。 Cov(X,X)就是X的方差(Variance).
【转】主成分分析(PCA)原理解析
本文转载于 http://www.cnblogs.com/jerrylead/archive/2011/04/18/2020209.html 主成分分析(Principal components analysis)-最大方差解释 在这一篇之前的内容是《Factor Analysis》,由于非常理论,打算学完整个课程后再写。在写这篇之前,我阅读了PCA、SVD和LD
PCA 在图像分析上的应用
同一物体旋转角度求取 直接上代码: import cv2, osimport numpy as npimport timedef perform_pca(image, num_components):# 将图像转换为浮点型img_float = np.float32(image)img_flatten = img_float.reshape(-1, 2)# 计算均值和协方差矩阵mean,
大规模数据的PCA降维
20200810 - 0. 引言 最近在做的文本可视化的内容,文本处理的方法是利用sklearn的CountVer+Tf-idf,这样处理数据之后,一方面数据的维度比较高,另一方面呢,本身这部分数据量也比较大。如果直接使用sklearn的pca进行降维,会很慢,而且pca也没有n_jobs来支持多线程工作。不过,我看到spark中已经支持的pca了,所以希望通过spark来实现这部分内容。