独立分量分析 ICA 等度量映射 ISOMAP 线性判别分析 LDA (拉普拉斯)数据降维方法 LE 局部线性嵌入 LLE 多维尺度变换MDS 主成分分析 PCA 核主成分分析 KPCA 稀疏主成分分析SPCA 奇异值分解SVD 特征矩阵的联合近似对角化 JADE 各种数据降维方法(matlab代码)代码获取戳此处代码获取戳此处 降维目的：克服维数灾难，获取本质特征，节省存储空

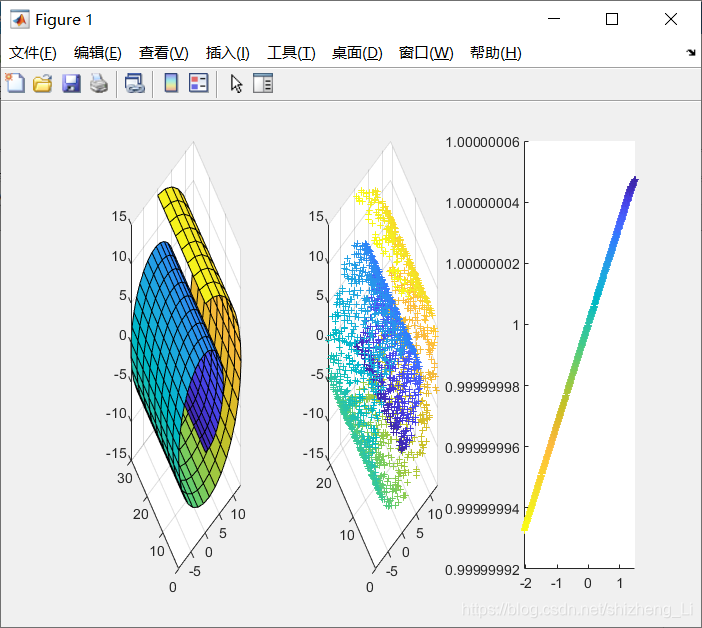
本文主要是学习LLE算法，可视化原作者给的例程，具体原理请移步参考。如有侵权，请联系删除。 文章目录 绘图结果代码参考 绘图结果 以上图片分别为运行代码：scurve_jian.m 和swissroll_jian.m文件得到，具体可以从参考文档中下载。 代码 lle.m % LLE ALGORITHM (using K nearest neighbors)%%

机器学习领域中所谓的降维就是指采用某种映射方法，将原高维空间中的数据点映射到低维度的空间中。降维的本质是学习一个映射函数 f : x->y，其中x是原始数据点的表达，目前最多使用向量表达形式。 y是数据点映射后的低维向量表达，通常y的维度小于x的维度（当然提高维度也是可以的）。f可能是显式的或隐式的、线性的或非线性的。 目前大部分降维算法处理向量表达的数据，也有一些降维算法处理高阶张量表达的数据