局部线性嵌入(LLE)算法matlab可运行

本文主要是介绍局部线性嵌入(LLE)算法matlab可运行，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本文主要是学习LLE算法，可视化原作者给的例程，具体原理请移步参考。如有侵权，请联系删除。

绘图结果

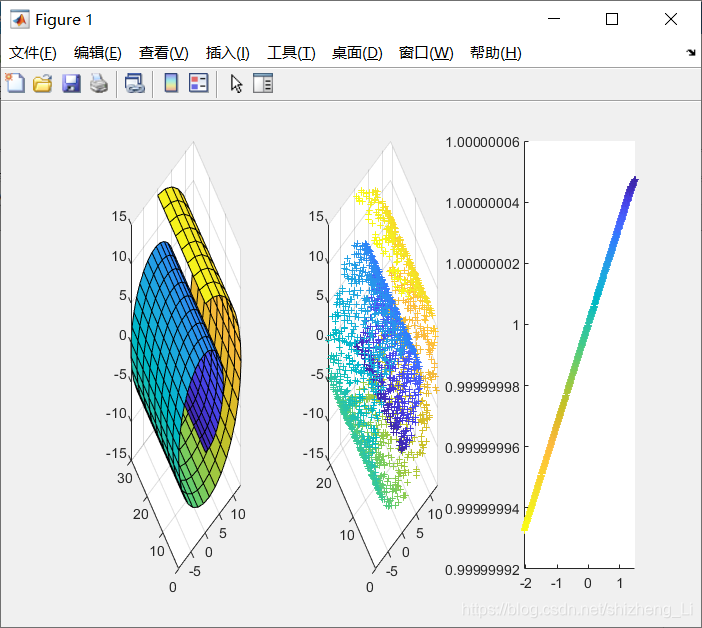
以上图片分别为运行代码：scurve_jian.m 和swissroll_jian.m文件得到，具体可以从参考文档中下载。

代码

lle.m

% LLE ALGORITHM (using K nearest neighbors)
%
% [Y] = lle(X,K,dmax)
%
% X = data as D x N matrix (D = dimensionality, N = #points)
% K = number of neighbors
% dmax = max embedding dimensionality
% Y = embedding as dmax x N matrix%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%function [Y] = lle(X,K,d)[D,N] = size(X);
fprintf(1,'LLE running on %d points in %d dimensions\n',N,D);% STEP1: COMPUTE PAIRWISE DISTANCES & FIND NEIGHBORS 
fprintf(1,'-->Finding %d nearest neighbours.\n',K);X2 = sum(X.^2,1);
distance = repmat(X2,N,1)+repmat(X2',1,N)-2*X'*X;[sorted,index] = sort(distance);
neighborhood = index(2:(1+K),:);% STEP2: SOLVE FOR RECONSTRUCTION WEIGHTS
fprintf(1,'-->Solving for reconstruction weights.\n');if(K>D) fprintf(1,'   [note: K>D; regularization will be used]\n'); tol=1e-3; % regularlizer in case constrained fits are ill conditioned
elsetol=0;
endW = zeros(K,N);
for ii=1:Nz = X(:,neighborhood(:,ii))-repmat(X(:,ii),1,K); % shift ith pt to originC = z'*z;                                        % local covarianceC = C + eye(K,K)*tol*trace(C);                   % regularlization (K>D)W(:,ii) = C\ones(K,1);                           % solve Cw=1W(:,ii) = W(:,ii)/sum(W(:,ii));                  % enforce sum(w)=1
end;% STEP 3: COMPUTE EMBEDDING FROM EIGENVECTS OF COST MATRIX M=(I-W)'(I-W)
fprintf(1,'-->Computing embedding.\n');% M=eye(N,N); % use a sparse matrix with storage for 4KN nonzero elements
M = sparse(1:N,1:N,ones(1,N),N,N,4*K*N); 
for ii=1:Nw = W(:,ii);jj = neighborhood(:,ii);M(ii,jj) = M(ii,jj) - w';M(jj,ii) = M(jj,ii) - w;M(jj,jj) = M(jj,jj) + w*w';
end;% CALCULATION OF EMBEDDING
options.disp = 0; 
options.isreal = 1; 
options.issym = 1; 
options.v0=ones(N,1); % 笔者新增的部分
[Y,eigenvals] = eigs(M,d+1,0,options);
Y = Y(:,1:d)'*sqrt(N); % bottom evect is [1,1,1,1...] with eval 0fprintf(1,'Done.\n');%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% other possible regularizers for K>D
%   C = C + tol*diag(diag(C));                       % regularlization
%   C = C + eye(K,K)*tol*trace(C)*K;                 % regularlization

swissroll_jian.m

% SWISS ROLL DATASETN=2000;K=12;d=2; % PLOT TRUE MANIFOLDtt0 = (3*pi/2)*(1+2*[0:0.02:1]); hh = [0:0.125:1]*30;xx = (tt0.*cos(tt0))'*ones(size(hh));yy = ones(size(tt0))'*hh;zz = (tt0.*sin(tt0))'*ones(size(hh));cc = tt0'*ones(size(hh));figuresubplot(1,3,1); surf(xx,yy,zz,cc);% GENERATE SAMPLED DATAtt = (3*pi/2)*(1+2*rand(1,N));  height = 21*rand(1,N);X = [tt.*cos(tt); height; tt.*sin(tt)];% SCATTERPLOT OF SAMPLED DATAsubplot(1,3,2); scatter3(X(1,:),X(2,:),X(3,:),12,tt,'+');% RUN LLE ALGORITHM
Y=lle(X,K,d);% SCATTERPLOT OF EMBEDDINGsubplot(1,3,3); scatter(Y(2,:),Y(1,:),12,tt,'+');

scurve_jian.m

% S-CURVE DATASETN=2000;K=12;d=2; % PLOT TRUE MANIFOLDtt = [-1:0.1:0.5]*pi; uu = fliplr(tt); hh = [0:0.1:1]*5;xx = [cos(tt) -cos(uu)]'*ones(size(hh));yy = ones(size([tt uu]))'*hh;zz = [sin(tt) 2-sin(uu)]'*ones(size(hh));cc = [tt uu]' * ones(size(hh));figure% 显示图形subplot(1,3,1);surf(xx,yy,zz,cc);shading flat% GENERATE SAMPLED DATAangle = pi*(1.5*rand(1,N/2)-1); angle_lr = fliplr(angle);height = 5*rand(1,N);X = [[cos(angle), -cos(angle_lr)]; height; [ sin(angle), 2-sin(angle_lr)]];% SCATTERPLOT OF SAMPLED DATAsubplot(1,3,2);scatter3(X(1,:),X(2,:),X(3,:),12,[angle angle_lr],'+');% RUN LLE ALGORITHM
Y=lle(X,K,d);% SCATTERPLOT OF EMBEDDINGsubplot(1,3,3); cla;scatter(Y(1,:),Y(2,:),12,[angle angle_lr],'+');

参考

[1]https://github.com/ArrowLuo/LLE_Algorithm
[2]https://cs.nyu.edu/~roweis/lle/code.html

这篇关于局部线性嵌入(LLE)算法matlab可运行的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---