本文主要是介绍显著提升!| (WOA)融合模拟退火和自适应变异的混沌鲸鱼优化算法应用于函数寻优,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
鲸鱼优化算法(whale optimization algorithm,WOA)是由Mirjalili和Lewis[1]于2016年提出的一种新型群体智能优化搜索方法,它源于对自然界中座头鲸群体狩猎行为的模拟,与其它群体智能优化算法相比,WOA算法结构新颖, 控制参数少,在许多数值优化和工程问题的求解中表现出较好的寻优性能,优于蚁群算法和粒子群算法等智能优化算法。
WOA算法在面对多变量复杂问题时也存在搜索效率低、收敛能力差、易陷入局部最优等缺点。因此,为提升WOA的优化性能,本文提出一个WOA的变体,即融合模拟退火和自适应变异的混沌鲸鱼优化算法。
00 文章目录
1 鲸鱼优化算法原理
2 改进的鲸鱼优化算法
3 代码目录
4 算法性能
5 源码获取
6 总结
01 鲸鱼优化算法原理
鲸鱼优化算法原理及其MATLAB代码获取方式在作者往期文章,这里不再赘述
02 改进的鲸鱼优化算法
2.1 混沌反向学习初始化种群
群体的算法的初始化影响其搜索性能。由于没有先验信息,WOA通常是由随机初始化产生的。这种策略在某种意义上是有用的。但是,有时候鲸鱼在搜索域中的分布并不均匀,这可能会使鲸鱼远离全局最优解,使收敛到最优解的搜索时间更长,导致收敛速度较低。混沌映射因具有随机性、灵敏性等特点,可以满足算法搜索的多样性。
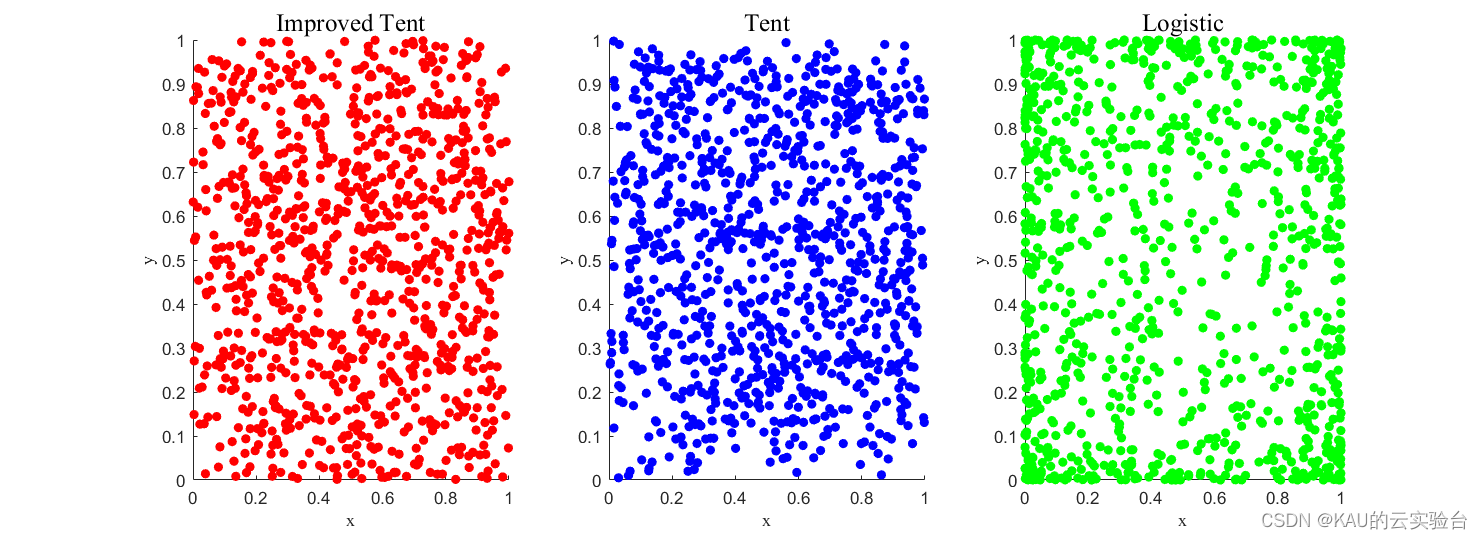
目前文献中常用的混沌扰动方程有Logistic映射和Tent映射等。由文献[3]可知Logistic映射的分布特点是:中间取值概率比较均匀,但在两端概率特别高,因此当全局最优点不在设计变量空间的两端时,对寻找最优点是不利的。而Tent混沌映射结构简单,具有比Logistic混沌映射更好的遍历均匀性和更快的搜索速度,同时,文献[2]已经从理论上证明了基于反向学习的种群初始化可以得到较好的初始解,进而加快收敛速度。因此,本文利用这两种初始化方法的优点,提出了基于混沌映射和反向学习的思想生成初始化种群。
考虑到 Tent 映射易在小循环周期和不动点上出现问题,为避免Tent混沌序列在迭代时落入小周期点和不稳定周期点,在典型Tent映射的表达式中添加随机数,即
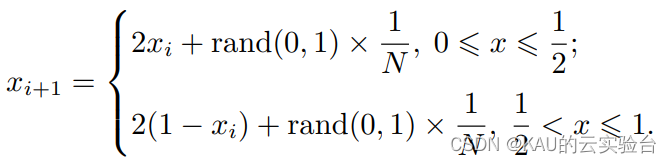
其中: N 是序列内粒子的个数。引入随机变量rand(0, 1) /N 不仅仍然保持了Tent混沌映射的随机性、遍历性、规律性,而且能够有效避免迭代落入小周期点和不稳定周期点内。
其次,利用该混沌序列Zkj生成对应的初始种群xij:
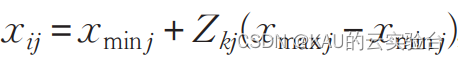
然后,生成反向种群x*ij:
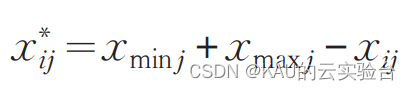
最后,比较初始种群和反向种群,选择适应度最优的N个个体组成初始种群,通过此初始化策略,能够在较为均匀分布的种群中进一步得到优质解,从而加快收敛速度。
2.2 非线性收敛因子
WOA算法中主要是两个系数参数A和C:
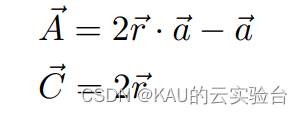
其中A主要取决于a,C主要取决于r。鲸鱼算法的全局勘探和局部开发都主要和A相关,换句话说,控制参数a对于算法的收敛速度和搜索精度起着至关重要的作用。当a较大时,算法具有较强的全局搜索能力,易于逃逸局部最优,但其局部开发能力弱,导致收敛速度下降。反之,如果a较小,则其局部开发能力较强,收敛速度加快,但易于陷入局部最优。
而在传统的WOA算法中,a从2到0线性递减,而在复杂优化问题中往往存在多个局部最优值,线性递减的策略反而会影响算法逃逸出局部最优的能力,因此本文重新提出一个非线性的收敛因子:

该非线性收敛因子a的仿真如图。
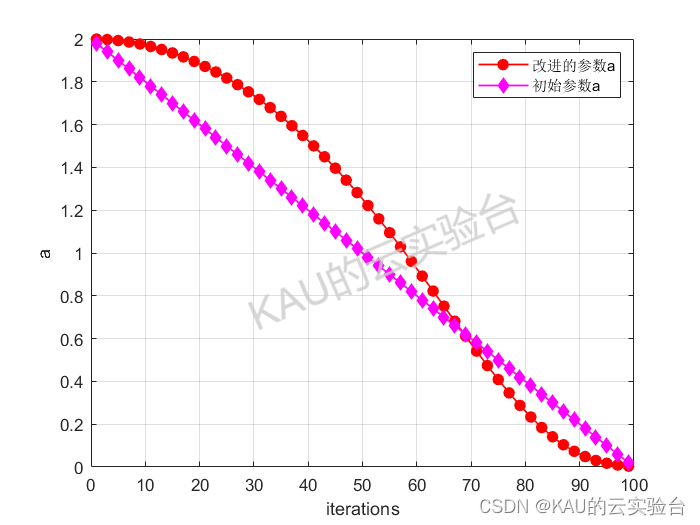
由图可以看出,在迭代前期,a 取值较大且衰减速度较慢,全局勘探能力较强,有利于避免种群陷入局部最优值。在迭代后期,a迅速衰减至较小的值,局部开发能力较强,有利于加速种群收敛。因此该非线性收敛因子更新策略可以更好地应用于非线性复杂优化问题的求解。
2.3 动态惯性权重
由于鲸鱼在螺旋更新位置的捕猎过程中猎物目标对鲸鱼群位置更新的影响不同,受文献[3]的启发本文提出一种动态惯性权值策略,公式如下:
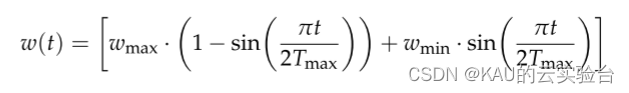
其中,wmax和wmin是权重变化的最大和最小值,Tmax为最大迭代次数,t为当前迭代次数。
于是螺旋位置更新公式变为:
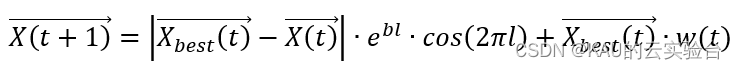
权重参数 ω 在迭代前期取得较大值,使鲸鱼算法具有较强的全局搜索能力,防止其陷入局部极值;在迭代后期取得较小值,此时鲸鱼算法有较强的局部搜索能力,可加速算法收敛得到最优解。
2.4 模拟退火操作及自适应变异扰动
模拟退火算法(Simulated Annealing,SA)由Metropolis在1953年提出[4],其特点为在一定的概率情况下保留劣质群体,增加种群的多样性,在一定程度上提高了跳出局部最优的能力。本文将模拟退火思想融入WOA算法中。
同时,考虑到迭代后期,由于搜索策略的原因,种群中所有鲸鱼个体都会向最优个体聚集,导致种群多样性降低。如果此时最优个体为局部最优解,则算法将出现早熟收敛。为了防止出现这类问题,本文提出了自适应的变异扰动,其公式如下:
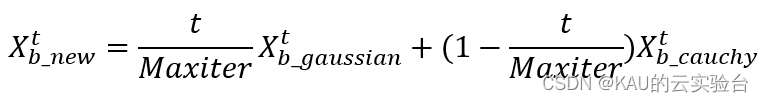
其中gaussian为高斯变异,cauchy为柯西变异。从上式可以看出,算法开始运行时,t值较小,柯西变异的权值较大,通过柯西变异获得较大步长,避免算法陷入局部最优解。随着算法不断运行,t 值较大, 高斯变异的权值较大,高斯变异杰出的局部搜索能力使得候选解在局部范围进行精确搜索,提高算法的寻优精度。
通过自适应的变异扰动产生新解,再凭借模拟退火算法能够以某种概率接受较差解的方式,跳出局部最优值,从而弥补WOA算法缺陷。
2.5 算法流程
本文的算法流程如下:
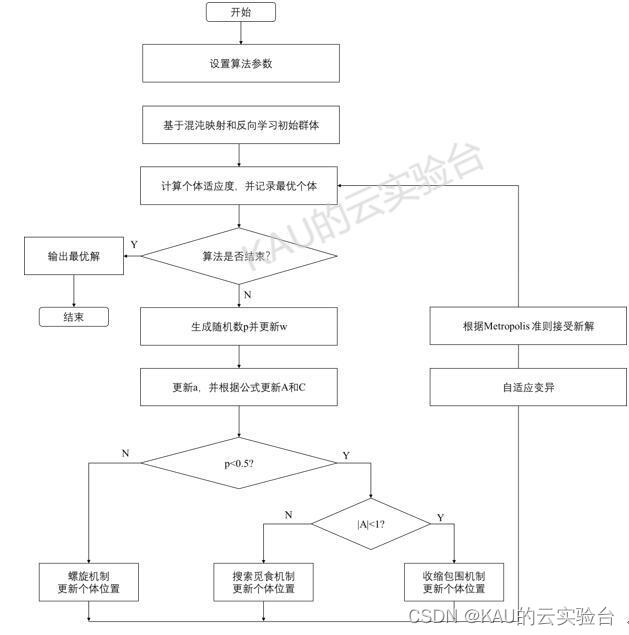
03 代码目录
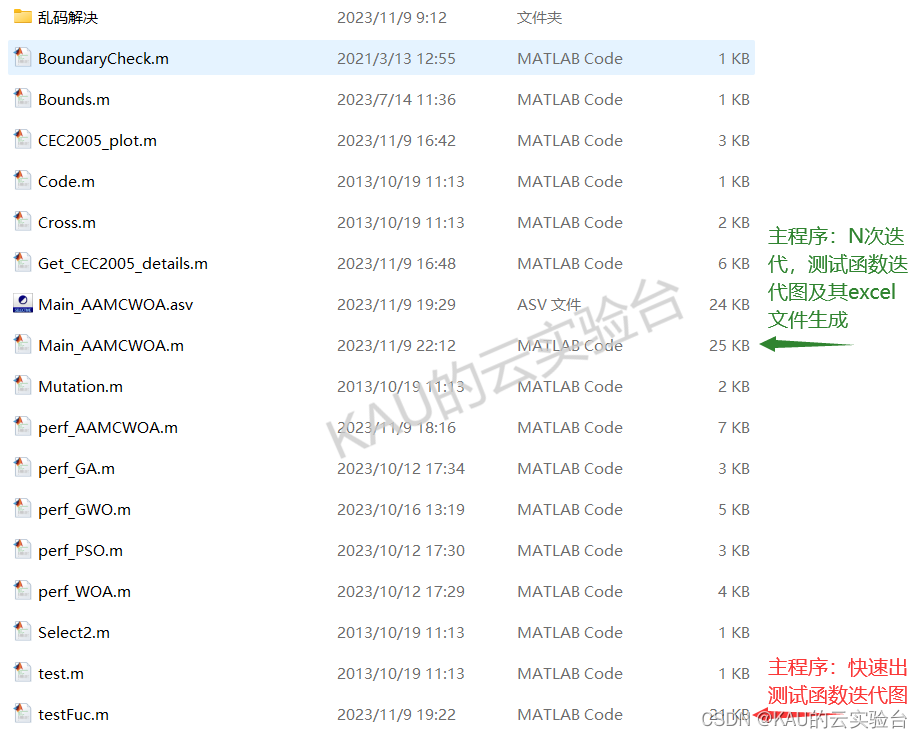
其中,Main_AAMCWOA.m为主程序,代码注释详细,一键运行Main_AAMCWOA即可得到所有运行结果,运行结果包括混沌序列比较图、控制参数比较图以及算法在各测试函数上的迭代图,最后将生成excel表,包含算法在各函数迭代n次的平均值,均值、运行时间、最优解。而testFuc.m则可以快速生成测试函数的迭代图。
同时,文件也有乱码解决,给出了主要代码的txt文件。
部分代码如下,改进部分会有特别注释。

生成的excel表如下
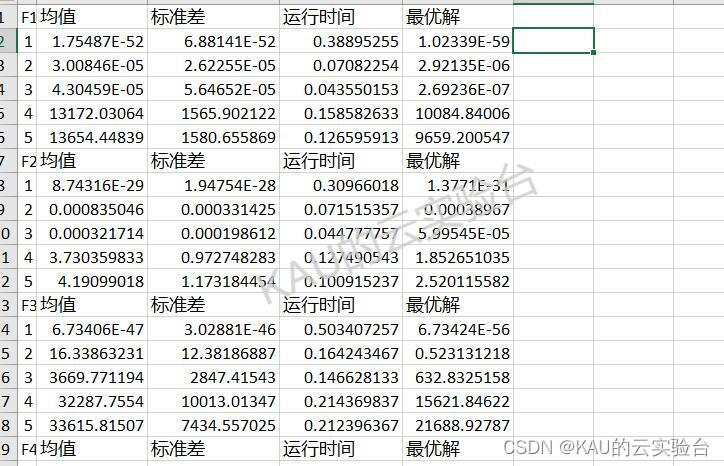
图中,1-5分别对应AAMCWOA、GWO、WOA、PSO、GA算法
04 算法性能
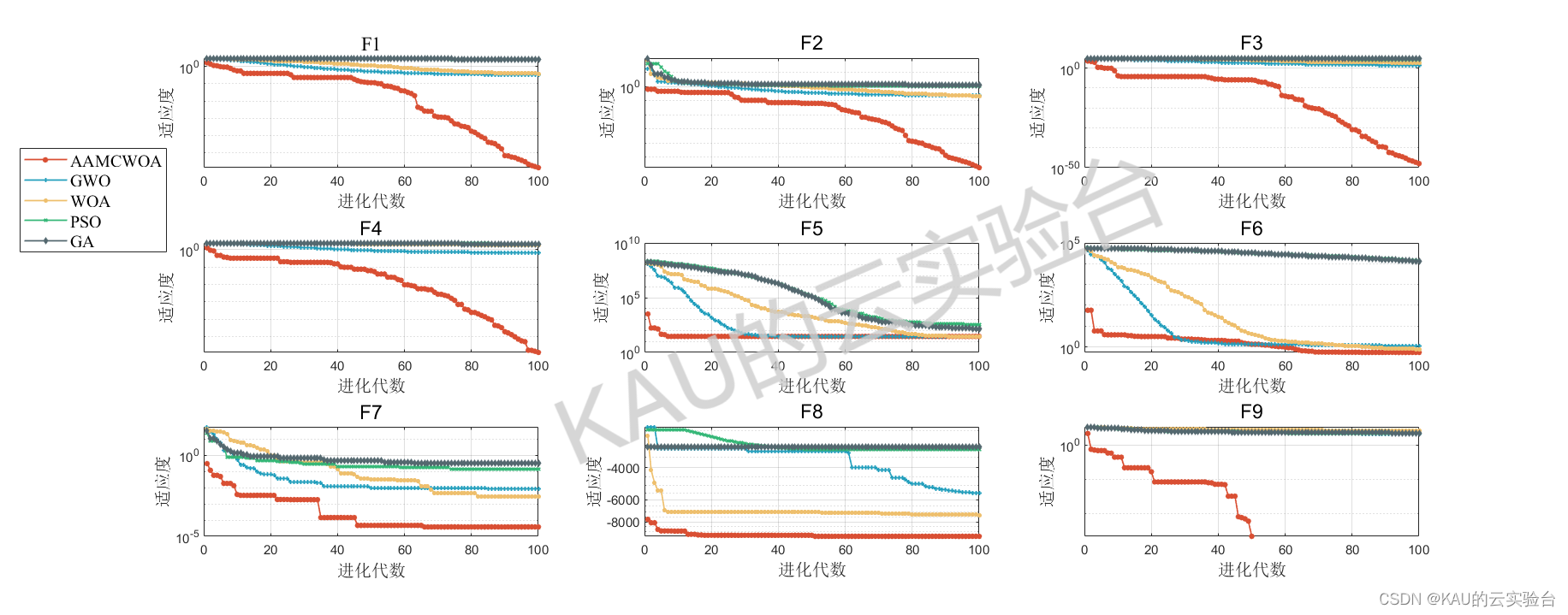
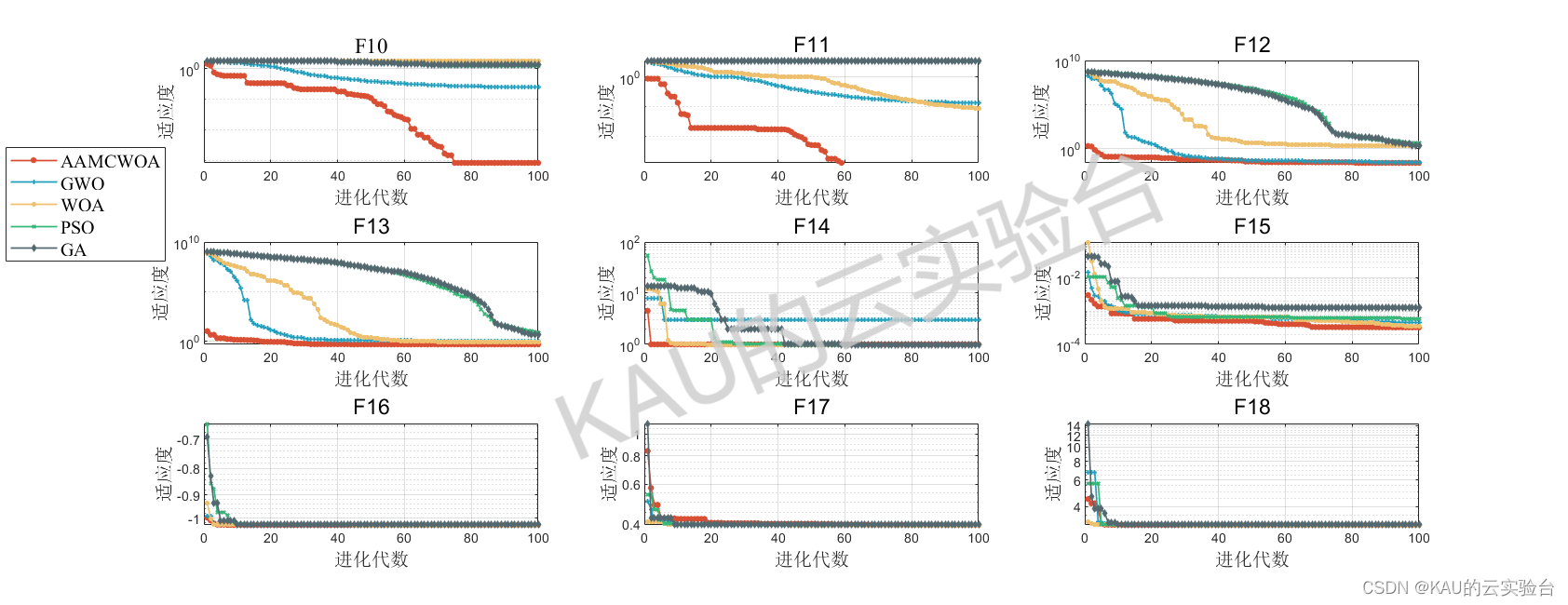
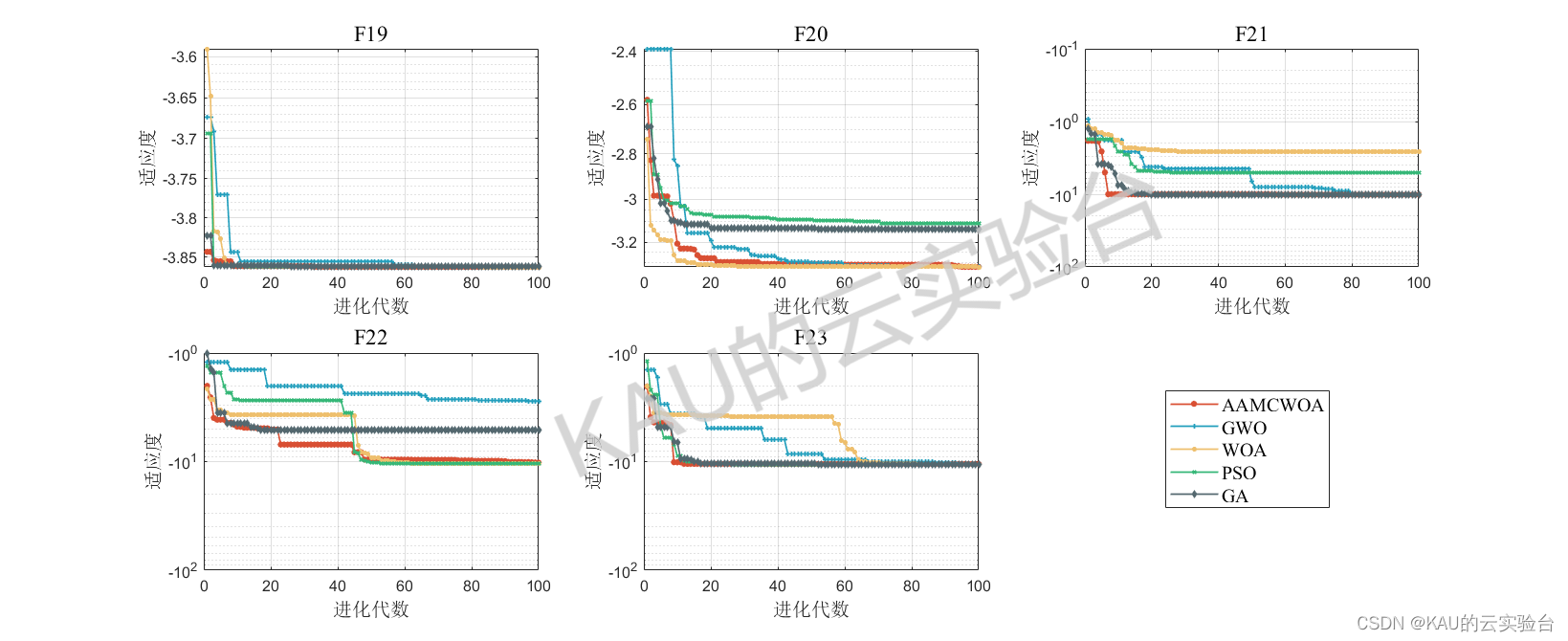
采用05年的标准测试函数来检验其寻优性能,该测试集是应用最多、最经典的测试集,包含23个Benchmark函数,其中F1-F5为单峰函数,F6-F12为基本的多峰函数,F13-F14为扩展的多峰函数,F15-F23为多峰组合函数,函数的具体信息如下:

其运行结果如下:
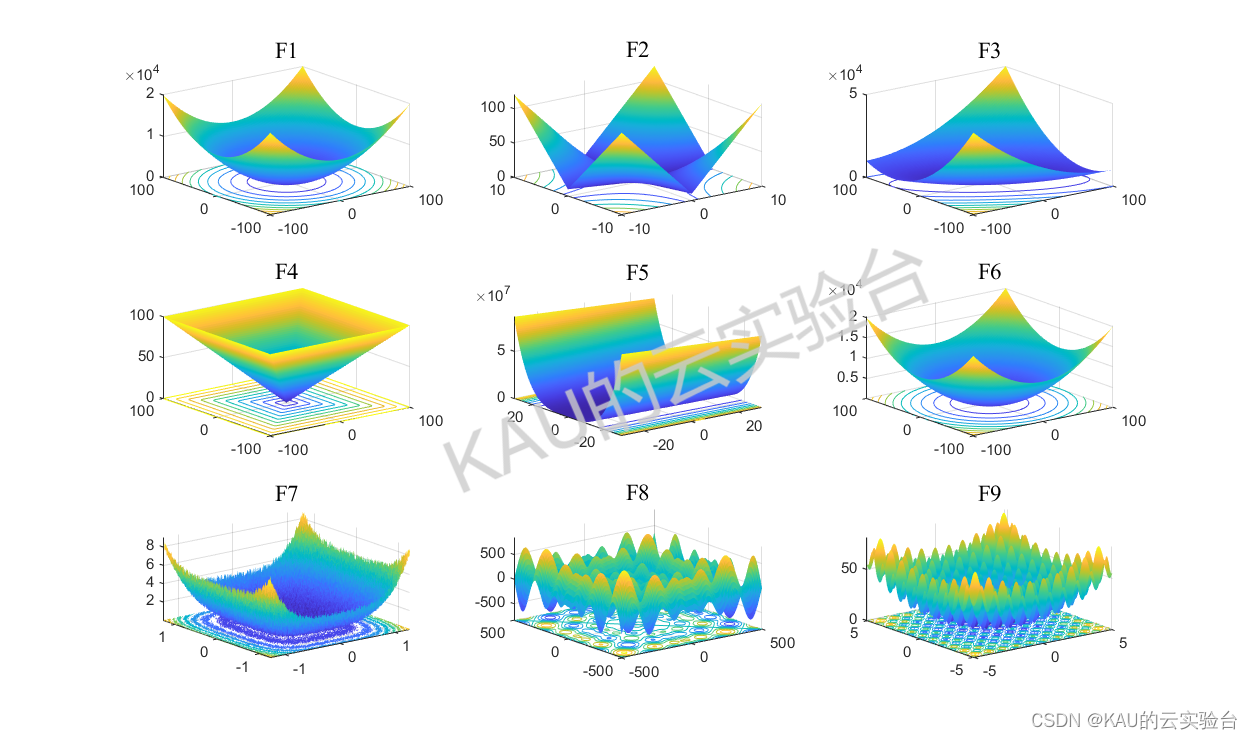
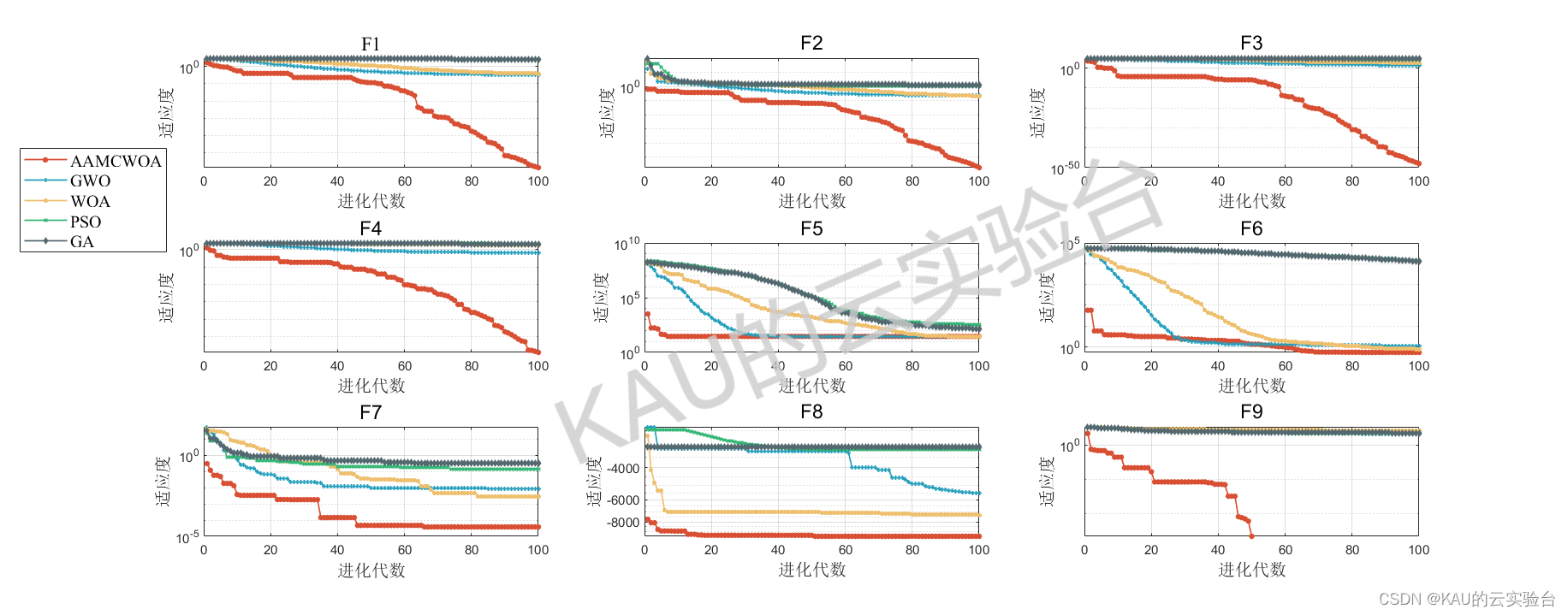
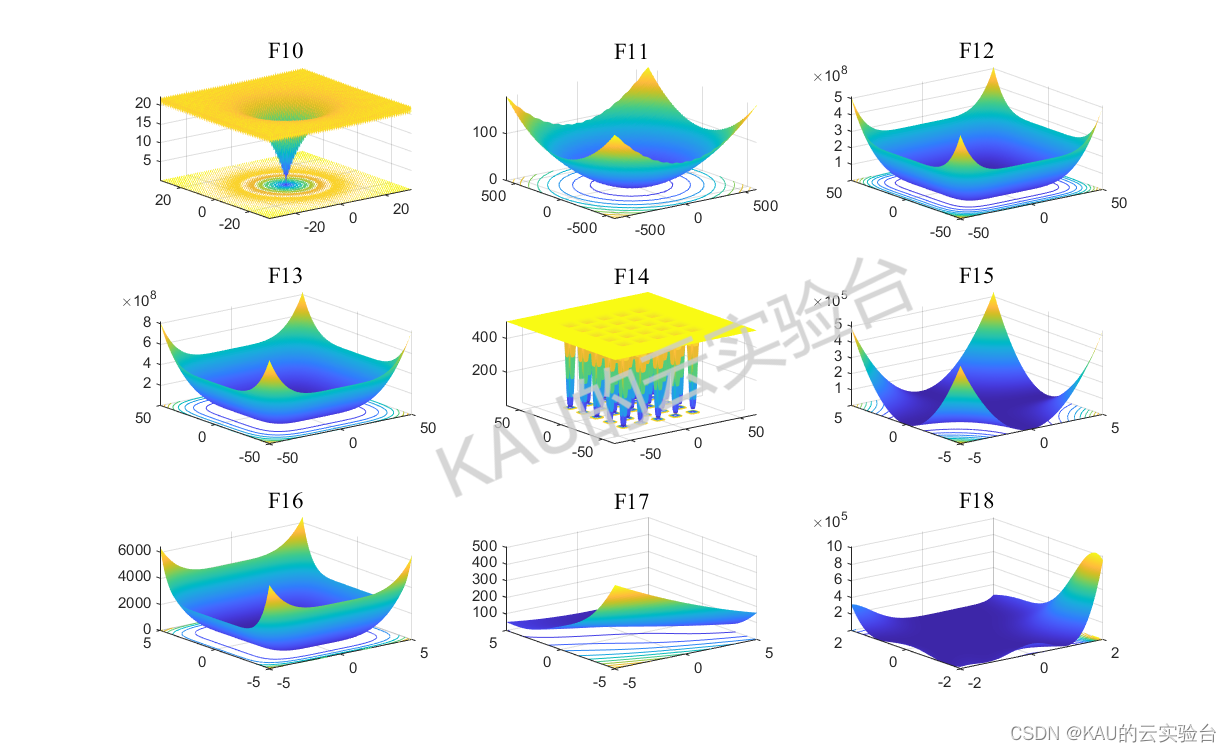
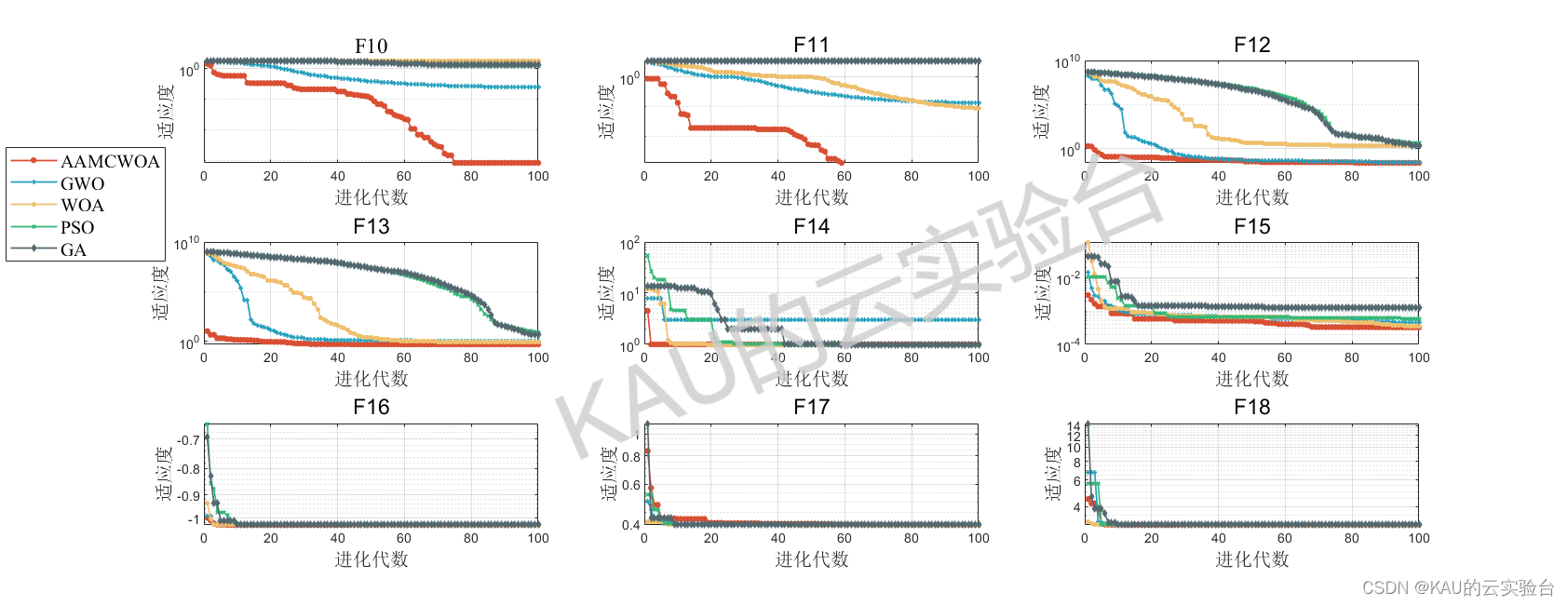
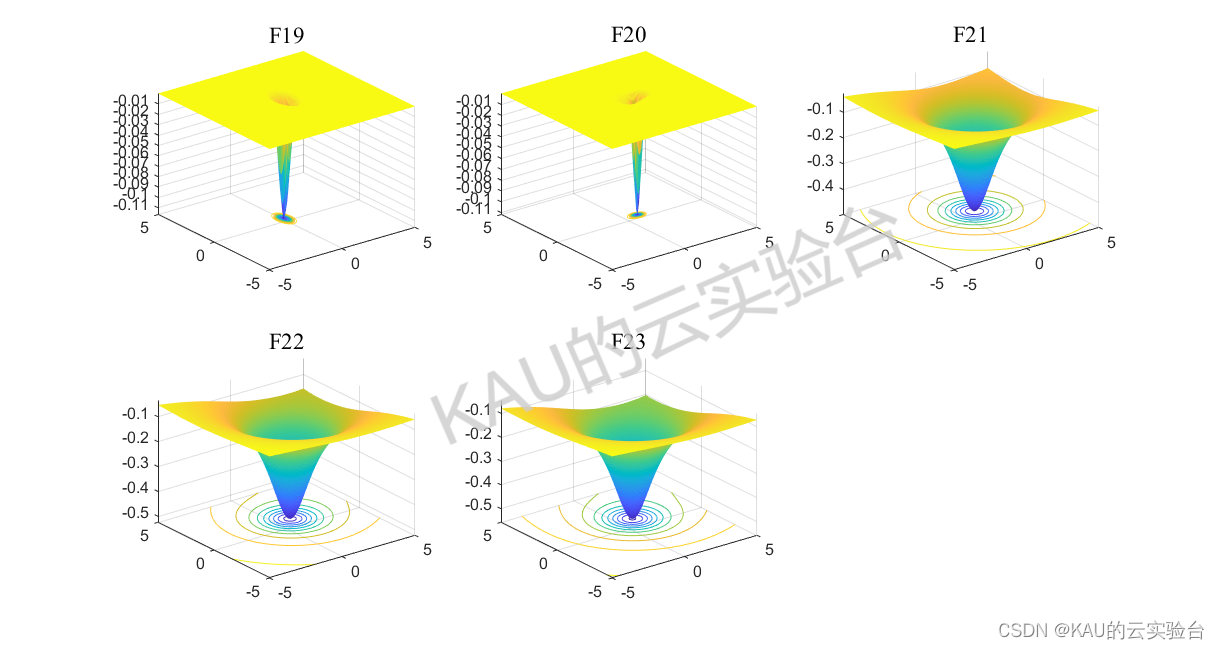
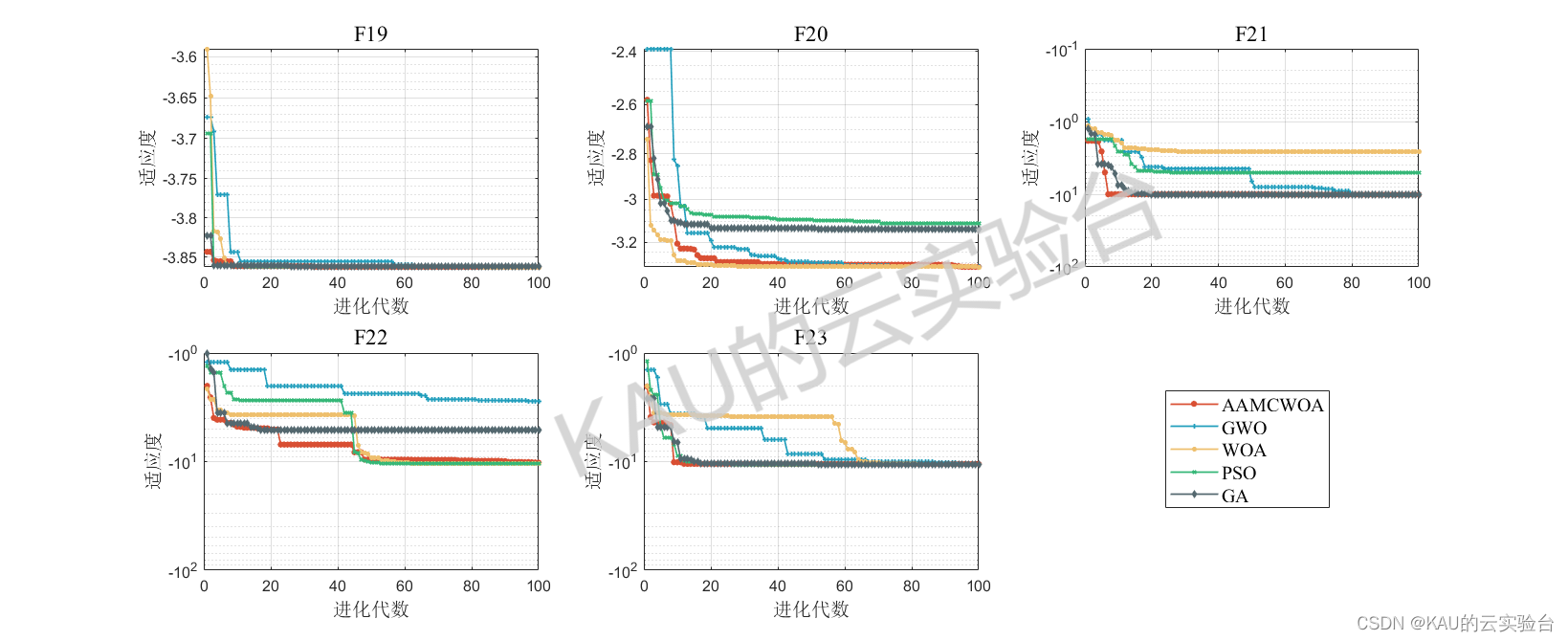
由结果可以看到,改进的鲸鱼优化算法在几乎所有函数的收敛速度和精度都更好,改进算法的效果良好。
05 源码获取
可在作者微信公众号获取:KAU的云实验台
注:文章中的所有图都可由程序直接运行出
06 总结
本文提出的改进鲸鱼优化算法具有良好的性能,改进有效,同时,本文的改进策略也可以进行推广,比如算法最后的模拟退火和自适应变异策略便可用于很多算法用来跳出局部最优,同时本文的改进也有进一步提升的空间,比如可以对鲸鱼优化算法的位置更新策略进一步改进,如加入Levy飞行、差分进化等。
参考文献
[1] MIRJALILI S,LEWIS A. The whale optimization algorithm[J].Advances in Engineering Software,2016,95:51一 67.
[2] 张强,李盼池.自适应分组混沌云模型蛙跳算法求解连续空间优化问题[J] .控制与决策,2015,30(5):923-928
[3] Y. Shi and R. Eberhart, “Modified particle swarm optimizer,” in Proc of
IEEE Icec Conference, 1999.
[4] DUPANLOU I,SCHNEIDER S,EXCOFFIER L. A simulated annealing approach to define the genetic struc⁃ ture of populations[J]. Molecular Ecology,2002,11 (12):2571 - 2581.
另:如果有伙伴有待解决的优化问题(各种领域都可),可以发我,我会选择性的更新利用优化算法解决这些问题的文章。
如果这篇文章对你有帮助或启发,可以点击右下角的赞/在看 (ง•̀_•́)ง(不点也行)
这篇关于显著提升!| (WOA)融合模拟退火和自适应变异的混沌鲸鱼优化算法应用于函数寻优的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


