本文主要是介绍【MATLAB源码-第70期】基于matlab的萤火虫算法(FA)的栅格路径规划,输出最短路径和适应度曲线。,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
操作环境:
MATLAB 2022a
1、算法描述
萤火虫算法(Firefly Algorithm,FA)是由剑桥大学的Xin-She Yang在2008年提出的一种元启发式优化算法。该算法的灵感来源于萤火虫闪烁的行为特征,主要用于解决连续的优化问题。萤火虫算法模仿自然界萤火虫发光吸引配偶或猎物的行为,将萤火虫个体的亮度与待优化问题的目标函数相关联。
萤火虫算法的基本原理
萤火虫算法基于以下几个简化的规则:
-
萤火虫的吸引力与亮度相关:在FA中,每个萤火虫的亮度代表解的质量(目标函数的值)。亮度越高的萤火虫对其他萤火虫具有较大的吸引力。
-
亮度与目标函数相关:通常情况下,萤火虫的亮度与目标函数值成正比。在最小化问题中,目标函数的值越小,萤火虫看起来越亮。
-
吸引力与距离相关:萤火虫的吸引力会随着距离的增加而减弱。通常使用指数衰减或其他函数来描述这种关系。
-
移动行为:一个萤火虫会朝着更亮的萤火虫移动,如果周围没有更亮的萤火虫,它将随机移动。
算法步骤
萤火虫算法的基本步骤如下:
-
初始化:随机生成一组萤火虫(解)的初始位置。
-
评估亮度:根据目标函数计算每个萤火虫的亮度。
-
更新位置:根据萤火虫间的相对亮度和吸引力,更新萤火虫的位置。
-
迭代过程:重复评估亮度和更新位置的步骤,直至满足终止条件,如达到最大迭代次数或解的质量不再提升。
2、仿真结果演示

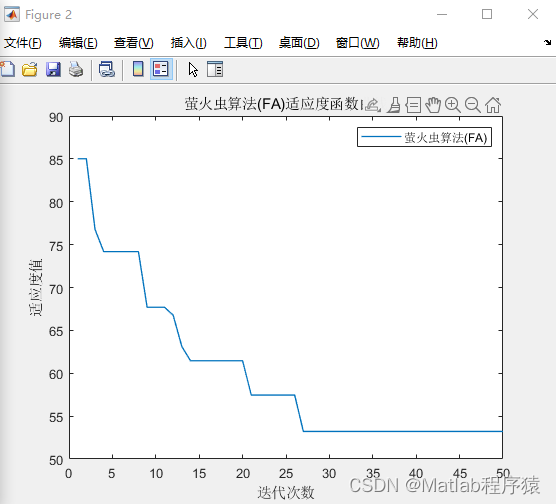
3、关键代码展示
略
4、MATLAB 源码获取
V
点击下方名片
这篇关于【MATLAB源码-第70期】基于matlab的萤火虫算法(FA)的栅格路径规划,输出最短路径和适应度曲线。的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




